
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 1. Елементи лінійної алгебриСтр 1 из 2Следующая ⇒
РОЗДІЛ 1. ЕЛЕМЕНТИ ЛІНІЙНОЇ АЛГЕБРИ Визначники Основні теоретичні відомості 1. Вираз
називають визначником (детермінантом) другого порядку.
2. Вираз
називають визначником (детермінантом) третього порядку. Для запам’ятовування цієї формули зручно користуватися схемою: + – 3. Основні властивості визначників. 3.1. Визначник не зміниться, якщо його рядки замінити відповідними стовпцями. 3.2. Визначник змінить знак на протилежний, якщо переставити місцями два рядки (два стовпці). 3.3. Спільний множник усіх елементів рядка (стовпця) можна винести за знак визначника. 3.4. Визначник дорівнює нулю, якщо: а) всі елементи рядка (стовпця) дорівнюють нулю; б) два рядки (стовпці) однакові; в) два рядки (стовпці) пропорційні. 3.5. Визначник не змінюється, якщо до елементів будь-якого рядка (стовпця) додати відповідні елементи іншого рядка (стовпця), помножені на одне й те саме число. 3.6. Визначник дорівнює сумі добутків елементів довільного рядка (стовпця) на їх алгебраїчні доповнення. Мінором
Визначники Приклади розв’язання типових задач
Приклад 1. Обчислити визначники: 1. а)
► 1. а) 2. На практиці зручно, коли частина елементів рядка (стовпця) дорівнює нулю (і чим більше нульових елементів, тим менше обчислень). Тому доцільно спочатку визначник перетворити так, щоб усі елементи деякого рядка (стовпця), крім одного, дорівнювали нулю, зазвичай використовуючи для цього властивості визначників (властивість 3.5). Тоді розклад визначника за елементами цього рядка (стовпця) містить лише один додаток. Приклад 2.
►
Вправи для самостійної роботи
Обчислити визначники:
1.
Розв’язати рівняння:
5.
Відповіді: 1. -27. 2. 12. 3. 1. 4. 180. 5. {0; -2}. 6. МАТРИЦІ Основні теоретичні відомості Прямокутну таблицю
яка складається з
Будь-якій квадратній матриці
Квадратну матрицю
Дії над матрицями
Нехай 1. Сумою матриць 2. Добутком довільного дійсного числа 3. Різницю матриць 4. Добуток матриць. Операція множення матриць існує лише для узгоджених матриць. Матриці
У загальному випадку Обернена матриця Для кожної невиродженої матриці
де Матричні рівняння Нехай потрібно знайти матрицю Помноживши справа обидві частини рівняння на обернену матрицю
Аналогічно
де
Ранг матриці Нехай задано матрицю Визначник порядку Рангом матриці
На практиці відшукання рангу ґрунтується на такому твердженні. Ранг матриці не зміниться, якщо над нею виконати елементарні перетворення: 1) переставити місцями два рядки (стовпці); 2) помножити кожен елемент рядка (стовпця) на ненульовий множник; 3) додати до елементів рядка (стовпця) елементи іншого рядка (стовпця), помножені на одне й те саме число. Скориставшись елементарними перетвореннями, матрицю можна звести до вигляду, коли всі її елементи, крім
Метод Крамера Нехай дано систему вигляду
де Головна матриця системи
Визначник цієї матриці
Якщо
де Якщо Якщо
Приклад 9. Розв’язати систему за формулами Крамера:
►
Відповідь: Зауважимо, що методом Крамера можна розв’язати систему, у якої кількість невідомих дорівнює кількості рівнянь і головний визначник Матричний метод СЛАР можна записати у вигляді:
де Якщо
Приклад 10. Розв’язати систему матричним методом:
►
Метод Гаусса
Метод Гаусса використовують для розв’язання СЛАР довільного вигляду. Процес розв’язання за методом Гаусса складається з двох етапів. Перший етап (прямий хід) ґрунтується на елементарних перетвореннях рядків системи, а саме, система залишається рівносильною початковій системі, якщо: 1) переставити місцями два рівняння; 2) помножити обидві частини рівняння на ненульовий множник; 3) додати почленно до рівняння елементи іншого рівняння, помножені на одне й те саме число. За допомогою таких перетворень СЛАР зводять до трапецевидного (або трикутного) вигляду:
На другому етапі (зворотний хід) послідовно визначають невідомі системи, рухаючись від останнього рівняння до першого. Проаналізуємо систему (A), в якій
Одержана система, отже, і початкова система, має єдиний розв’язок, який визначаємо так. Спочатку з останнього рівняння знайдемо Якщо 1) хоча б одне з чисел 2) усі числа Оскільки СЛАР взаємно однозначно відповідає розширена матриця, то елементарні перетворення рівнянь системи рівносильні перетворенню рядків розширеної матриці. Тому при розв’язуванні СЛАР за методом Гаусса будемо працювати тільки з розширеною матрицею.
Критерій сумісності СЛАР Нехай задано систему вигляду:
Складемо головну і розширену матриці цієї системи
Теорема Кронекера - Капеллі Для того, щоб СЛАР була сумісна, необхідно і достатньо, щоб ранг Якщо ранг головної матриці дорівнює рангу розширеної матриці і дорівнює кількості невідомих, то система має єдиний розв’язок. Якщо ранг головної матриці дорівнює рангу розширеної матриці, але менший від кількості невідомих, то система має безліч розв’язків.
Якщо
Приклад 11. Розв’язати систему за методом Гауса.
► Записуємо розширену матрицю системи і, виконуючи елементарні перетворення над рядками, зводимо її до ступінчатого вигляду:
r(A) = r(B) = 4 = n (n – кількість невідомих) => система сумісна. Останній рядок відповідає рівнянню
Далі записуємо рівняння:
Отже, розв’язок системи:
Приклад 12.
►
Розв’язання аналогічне завданню (1).
~
r(A) = r(B) = 3 < n = 4. Задана система має безліч розв’язків. Рухаючись від останнього рівняння до першого, послідовно знаходимо:
Відповідь:
Вправи для самостійної роботи Розв’язати системи рівнянь:
1.
Розв’язати системи рівнянь, використавши метод Гаусса:
3.
Відповіді: 1. 4.
ВЕКТОРИ ЛІНІЇ ПЕРШОГО ПОРЯДКУ КРИВІ ДРУГОГО ПОРЯДКУ ПЛОЩИНА РОЗДІЛ 1. ЕЛЕМЕНТИ ЛІНІЙНОЇ АЛГЕБРИ Визначники
|
||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.19.251 (0.104 с.) |




 елемента
елемента  визначника називають визначник, утворений із даного визначника викреслюванням
визначника називають визначник, утворений із даного визначника викреслюванням  -го рядка та
-го рядка та  -го стовпця. Алгебраїчним доповненням
-го стовпця. Алгебраїчним доповненням  елемента
елемента  :
: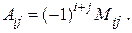
 -го порядку обчислюють, використовуючи властивості 3.6 та 3.5.
-го порядку обчислюють, використовуючи властивості 3.6 та 3.5.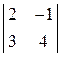 ; б)
; б)  ; 2.
; 2.  ; 3.
; 3.  .
.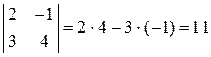 . б)
. б) 
 ◄
◄
 Приклад 3.. Розв’язати рівняння:
Приклад 3.. Розв’язати рівняння:
 ◄
◄ . 2.
. 2.  3.
3.  4.
4. 
 6.
6. 
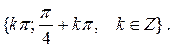

 елементів
елементів 
 можна поставити у відповідність визначник
можна поставити у відповідність визначник  (або
(або  , | А|)
, | А|)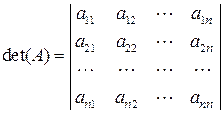
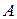 , визначник якої не дорівнює нулю, називають невиродженою. Якщо
, визначник якої не дорівнює нулю, називають невиродженою. Якщо  , то матрицю
, то матрицю 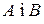 - матриці однакової розмірності.
- матриці однакової розмірності. є матриця
є матриця  рівна
рівна  .
.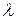 на матрицю
на матрицю  є матриця
є матриця  .
.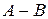 визначають, як суму матриці
визначають, як суму матриці  помноженої на
помноженої на  :
:  .
.

 .
. існує обернена матриця
існує обернена матриця 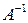 .
.  , де
, де

 - алгебраїчне доповнення елемента
- алгебраїчне доповнення елемента  .
. , що задовольняє матричне рівняння
, що задовольняє матричне рівняння  , де
, де 

 рядків і стільки ж стовпців, де
рядків і стільки ж стовпців, де  .
. або
або  .
.
 , дорівнюють нулю. Тоді ранг матриці дорівнює
, дорівнюють нулю. Тоді ранг матриці дорівнює  . Якщо матрицю звести до верхньої трикутної або трапецевидної, то ранг матриці А дорівнює кількості ненульових рядків (див. приклад 5).
. Якщо матрицю звести до верхньої трикутної або трапецевидної, то ранг матриці А дорівнює кількості ненульових рядків (див. приклад 5). (1)
(1) – невідомі змінні.
– невідомі змінні.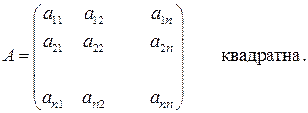
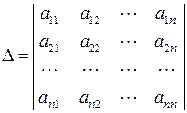 (2)
(2) , то система (1) має єдиний розв’язок, який можна знайти за формулами Крамера
, то система (1) має єдиний розв’язок, який можна знайти за формулами Крамера
 одержуємо відповідно заміною стовпчика коефіцієнтів при невідомому
одержуємо відповідно заміною стовпчика коефіцієнтів при невідомому  в (2) на стовпчик вільних членів.
в (2) на стовпчик вільних членів.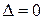 , а принаймні один із визначників
, а принаймні один із визначників  , то система (1) несумісна.
, то система (1) несумісна.

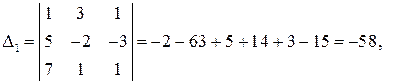




 ◄
◄

 і
і 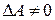 , то єдиний розв’язок системи можна знайти за формулою
, то єдиний розв’язок системи можна знайти за формулою






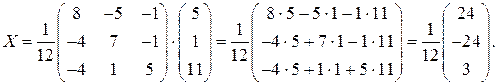
 ◄
◄ (A)
(A) , то система (A) набирає трикутного вигляду
, то система (A) набирає трикутного вигляду
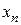 , після цього з передостаннього рівняння знайдемо
, після цього з передостаннього рівняння знайдемо 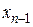 ; піднімаючись по системі від останнього рівняння до першого, знайдемо всі інші невідомі.
; піднімаючись по системі від останнього рівняння до першого, знайдемо всі інші невідомі. , то може бути два випадки:
, то може бути два випадки: не дорівнює нулю. Тоді система не має розв’язків, тобто несумісна;
не дорівнює нулю. Тоді система не має розв’язків, тобто несумісна;
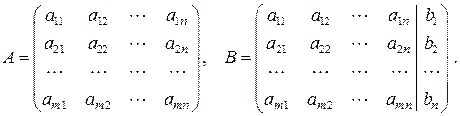
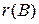 розширеної матриці
розширеної матриці  , то система несумісна.
, то система несумісна.
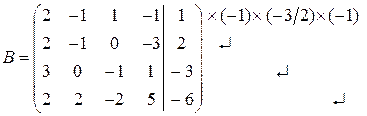 ~
~ ~
~  ~
~ ~
~  .
. звідки
звідки 

 ◄
◄
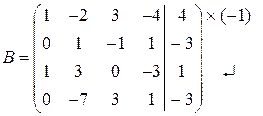 ~
~  ~
~ ~
~ 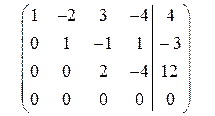 ~
~ 
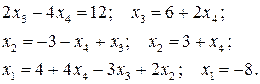
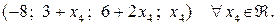 ◄
◄ 2.
2. 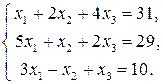
 , 4.
, 4.  , 5.
, 5.  .
. 2.
2. 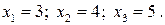 3.
3.  .
. де
де 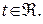 5.
5. 



