Роль модели и адекватность модели

Построив модель, исследователь может:

• прогнозировать свойства и поведение объекта как внутри области, в которой построена модель, так и (при обоснованном применении) за её пределами (прогнозирующая роль модели);
• управлять объектом, отбирая наилучшие воздействия путём испытания их на модели (управляющая роль);
• познавать явление или объект, модель которого он построил (познавательная роль модели);
• получать навыки по управлению объектом путём использования модели как тренажёра или игры (обучающая роль);
• улучшать объект, изменяя модель и испытывая её (проектная роль).

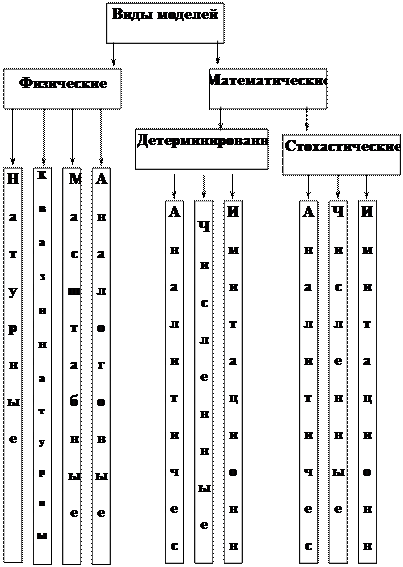
Поскольку модель является выражением конечного ряда и только важнейших для конкретного исследования аспектов сущности, то она не может быть абсолютно идентичной моделируемому объекту. Кроме этого, реальный объект бесконечен для познания. Поэтому нет смысла стремиться к бесконечной точности при построении модели. Для выяснения необходимой степени адекватности обычно строят ряд моделей, начиная с грубых, простых моделей и двигаясь ко все более сложным и точным. Как только затраты на построение очередной модели начинают превышать планируемую отдачу от модели, то уточнение модели прекращают. Первоначальные шаги производятся в каком-либо существующем универсальном моделирующем пакете. После одобрения модели под неё пишется специализированный пакет. Необходимость в этом возникает в случае, если функционирование модели в универсальной среде моделирования не удовлетворяет требованиям быстродействия (или каким-то другим).

Моделирование — прикладная инженерная наука класса технологических. Моделирование — дисциплина, ставящая целью построение моделей и их исследование посредством собственных универсальных методов, а также специфических методов смежных с ней наук (математика, исследование операций, программирование).

Физические(материальные) и математические модели.

Физические модели

В основу классификации положена степень абстрагирования модели от оригинала. Предварительно все модели можно подразделить на две группы: материальные (физические) и абстрактные (математические) (рис. 9.1).

Физической моделью обычно называют систему, которая эквивалентна или подобна оригиналу, либо у которой процесс функционирования такой же, как у оригинала, и имеет ту же или другую физическую природу. Можно выделить следующие виды физических моделей: натурные, квазинатурные, масштабные и аналоговые.

Натурные модели – это реальные исследуемые системы. Их на­зывают макетами и опытными образцами. Натурные модели имеют полную адекватность с системой-оригиналом, что обеспечивает высокую точность и достоверность результатов моделирования. Процесс проектирования систем завершается зачастую испытанием опытных образцов.

 

Рис. 9.1. Классификация моделей

Квазинатурные модели представляют собой совокупность натурных и математических моделей [4]. Этот вид моделей используется в случаях, когда математическая модель части системы не является удовлетворительной (например, модель человека-оператора) или когда часть системы должна быть исследована во взаимодействии с остальными частями, но их еще не существует, либо их включение в модель затруднено или дорого. Примерами квазинатурных моделей могут служить вычислительные полигоны, на которых отрабатывается программное обеспечение различных систем, или реальные АСУ, исследуемые совместно с математическими моделями соответствующих производств [5

Масштабная модель – это система той же физической природы, что и оригинал, но отличающаяся от него масштабами. Методологической основой масштабного моделирования является теория подобия, которая предусматривает соблюдение геометрического подобия оригинала и модели и соответствующих масштабов для их параметров. При проектировании систем масштабные модели могут использоваться для анализа вариантов компоновочных решений по конструкции системы и ее элементов.

Аналоговыми моделями называются системы, имеющие физическую природу, отличающуюся от оригинала, но сходные с оригиналом процессы функционирования. Обязательным условием при этом является однозначное соответствие между параметрами изучаемого объекта и его модели, а также тождественность безразмерных математических описаний процессов, протекающих в них. Для создания аналоговой модели требуется наличие мате­матического описания изучаемой системы. Аналоговые модели используют при исследовании средств вычислительной техники на уровне логических элементов и элек­трических цепей, а также на системном уровне, когда функциони­рование системы описывается, например, дифференциальными или алгебраическими уравнениями.

Математические модели

Математическая модель представляет собой формализованное описание системы с помощью абстрактного языка, в частности, с помощью математических соотношений, отражающих процесс функционирования системы. Для составления модели можно использовать любые математические средства – алгебраическое, дифференциальное и интегральное исчисление, теорию множеств, теорию алгоритмов и т.д. По существу, вся математика создана для составления и исследования моделей объектов или процессов.

Цели моделирования и характерные черты оригинала определяют, в конечном счете, ряд других особенностей моделей и методы их исследования. Например, математические модели можно классифицировать на детерминированные и вероятностные (стохастические).

Первые устанавливают однозначное соответствие между параметрами и характеристиками модели, а вторые – между статистическими значениями этих величин. Выбор того или иного вида модели обусловлен степенью необходимости учета случайных факторов.

Среди математических моделей можно выделить по методу их исследования аналитические, численные и имитационные модели.

Аналитической моделью называется такое формализованное описание системы, которое позволяет получить решение уравнения в явном виде, используя известный математический аппарат.

Численная модель характеризуется зависимостью такого вида, который допускает только частные численные решения для конкретных начальных условий и количественных параметров модели.

Имитационная модель – это совокупность описания системы и внешних воздействий, алгоритмов функционирования системы или правил изменения состояния системы под влиянием внешних и внутренних возмущений. Эти алгоритмы и правила не дают возможности использовать имеющиеся математические методы аналитического и численного решения, но позволяют имитировать процесс функционирования системы и производить измерения интересующих характеристик.

Имитационные модели могут быть созданы для гораздо более широкого класса объектов и процессов, чем аналитические и численные модели. Поскольку для реализации имитационных моделей используются, как правило, вычислительные системы, средствами формализо­ванного описания имитационных моделей служат, зачастую, уни­версальные или специальные алгоритмические языки.

 

Выбор метода моделирования

Аналитические методы

Разработанная математическая модель функционирования системы может быть исследована различными методами – аналитическими или имитационными. С помощью аналитических методов анализа можно провести наиболее полное исследование модели. Для использования аналитических методов необходимо математическую модель преобразовать к виду явных аналитических зависимостей между характеристиками и параметрами системы и внешних воздействий. Однако это удается лишь для сравнительно простых систем. Применение аналитиче­ских методов для более сложных систем связано с большей, по сравнению с другими методами, степенью упрощения реальности и абстрагирования. Поэтому аналитические методы исследования используются обычно для первоначальной грубой оценки характеристик всей системы или отдельных ее подсистем, а также на ранних стадиях проектирования систем, когда недостаточно информации для построения более точной модели.

Имитационные методы

Имитационное моделирование является наиболее универсальным методом исследования систем и количественной оценки характеристик их функционирования. При имитационном моделировании динамические процессы системы-оригинала подменяются процессами, имитируемыми в абстрактной модели, но с соблюдением таких же соотношений длительностей и временных последовательностей отдельных операций. Поэтому метод имитационного моделирования мог бы называться алгоритмическим или операционным. В процессе имитации, как при эксперименте с оригиналом, фиксируют определенные события и состояния или измеряют выходные воздействия, по которым вычисляют характеристики качества функционирования системы. Имитационное моделирование позволяет рассматривать процессы, происходящие в системе, практически на любом уровне детализации. Используя алгоритмические возможности ПК, в имитационной модели можно реализовать любой алгоритм управления или функционирования системы.

Численные методы

Численное моделирование допускает только частные численные решения для конкретных начальных условий и количественных параметров модели.

Модели, которые допускают исследование аналитическими методами, также могут анализироваться имитационными методами. Все это является причиной того, что имитационные методы моделирования становятся основ­ными методами исследования сложных систем.

Методы имитационного моделирования различаются в зависимости от класса исследуемых систем, способа продвижения модельного времени и вида количественных переменных параметров системы и внешних воздействий.

В первую очередь можно разделить методы имитационного моделирования дискретных и непрерывных систем. Если все элементы системы имеют конечное множество состояний, и переход из одного состояния в другое осуществляется мгновенно, то такая система относится к системам с дискретным изменением состояний, или дискретным системам. Если переменные всех элементов системы изменяются постепенно и могут принимать бесконечное множество значений, то такая система называется системой с непрерывным изменением состояний, или непрерывной системой. Системы, у которых имеются переменные того и другого типа, считаются дискретно-непрерывными.

Особое значение имеет стационарность или нестационарность случайных, независимых переменных системы и внешних воздей­ствий. При нестационарном характере переменных, в первую очередь внешних воздействий, что часто наблюдается на прак­тике, должны быть использованы специальные методы моделиро­вания, в частности, метод повторных экспериментов.

Еще одним классификационным параметром следует считать схему формализации, принятую при создании математической модели. Здесь, прежде всего, необходимо разделить методы, ориентированные на алгоритмический (программный) или структурный (агрегатный) подход. В первом случае процессы управляют элементами (ресурсами) системы, а во втором – элементы управляют процессами, определяют порядок функционирования системы.