
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сформулируйте основные механизмы безопасности данных в компьютерных сетяхСодержание книги
Поиск на нашем сайте
Вопрос такой же
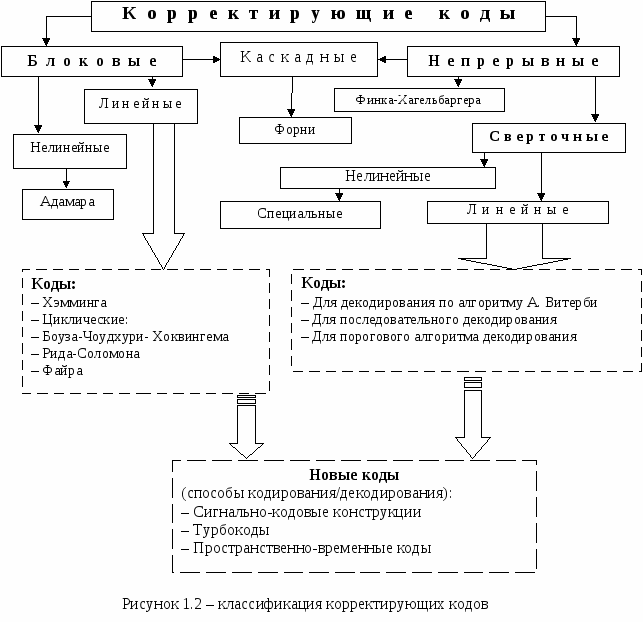
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи. Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды). По способу формирования КК подразделяются на блоковые и непрерывные. Формирование блоковых кодов предусматривает разбиение передаваемыхцифровых последовательностейна отдельные блоки, которые подаются на вход кодера. Каждому такому блоку на выходе кодера соответствует блок кодовых символов, работа кодера определяется правилом, или алгоритмом кодирования. формирование непрерывных кодов осуществляетсянепрерывно во времени, без разделения на блоки, что и определяет наименование этого класса кодов. Блоковые коды исторически были предложены и изучены ранее, на заре развития теории кодирования. В классе непрерывных кодов следует отметить сверточные коды, которые по характеристикам превосходят блоковые коды, и, по этой причине, находят широкое применение в телекоммуникационных системах. Многие коды носят имена ученых, которые их предложили и исследовали. Таким примером является непрерывный код Финка-Хагельбаргера, предложенный советским ученым Л.М. Финком и немецким специалистом Р. Хагельбаргером. Длительное время этот код служил в литературе показательным примером непрерывного кода с простым алгоритмом кодирования/декодирования, но после открытия сверточных кодов уступил им место. Для описания процедур кодирования/декодирования как блоковых, так и сверточных кодов используют адекватный математический аппарат. Для описания линейных кодов используется хорошо разработанный аппарат линейной алгебры. Формирование нелинейных кодов производится с применением нелинейных процедур. Такой подход позволяет в некоторых случаях получить нелинейные коды с рядом специальных свойств. В теории и технике кодирования важной является проблема сложности реализации процедур кодирования/декодирования и, в особенности, процедур декодирования. Поэтому некоторые классы кодов (коды Хемминга, циклические коды Боуза-Чоудхури-Хоквингема, Рида-Соломона, Файра и др.) были разработаны совместно с алгоритмами декодирования, связанными со структурными свойствами этих кодов. И, наоборот, разработка новых алгоритмов декодирования сверточных кодов (алгоритм А. Витерби, последовательное декодирование, пороговое декодирование) инициировала поиски соответствующих сверточных кодов. Отличительные преимущества корректирующих кодов (как блоковых, так и сверточных) побуждали поиски новых подходов к реализации путей повышения помехоустойчивости и эффективности телекоммуникационных систем. На рис. 1.2 отмечены, соответственно, новые методы кодирования: сигнально-кодовые конструкции, турбокоды, пространственно-временные коды и т.п.
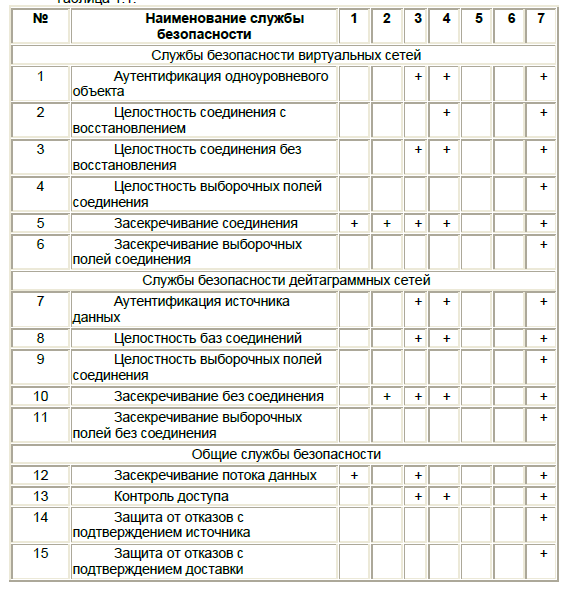
Классификация групп защиты Защита объектов ВС. С каждым объектом ВС связана некоторая информация, однозначно идентифицирующаяся ею. Это могут быть число, строка, символ, алгоритм, подтверждающие подлинность объекта. Эта информация определяется как идентификатор. Процесс проверки этого идентификатора называется идентификацией объекта. Если объект имеет некоторый идентификатор, зарегистрированный в сети, он называется легальным объектом; остальные объекты относятся к нелегальным. После того как объект идентифицирован и верифицирован (подтверждена его подлинность) - процедура идентификации объекта считается завершенной. Следующим шагом является установление сферы действия объекта и доступных ему ресурсов ВС. Такая процедура называется предоставлением полномочий. Перечисленные три процедуры инициализации относятся непосредственно к объекту ВС и относятся к средствам защиты самого объекта. Следующая совокупность функций защиты - это подтверждение подлинности соединения объектов по линиям связи. Эти функции называются взаимоподтверждением подлинности. Процедура подтверждения подлинности выполняется обычно в самом начале сеанса в процессе установления соединения. Цель - обеспечить высокую степень уверенности, что соединение установлено с равноправным объектом и вся информация, предназначенная для обмена, верифицирована и подтверждена. После установления соединения необходимы следующие четыре процедуры, чтобы обеспечить защиту при обмене сообщениями: а) получатель должен быть уверен в истинности источника данных подтверждение подлинности идентификатора и отправителя; б) получатель должен быть уверен в истинности передачи данных; в) отправитель должен быть уверен в доставке данных получателю;
г) отправитель должен быть уверен в истинности доставленных данных (расписка в получении). Защита баз данных ВС. Защита БД означает защиту самих данных и их контролируемое использование на рабочих ЭВМ сети, а также защиту любой сопутствующей информации, которая может быть извлечена или сгенерирована из этих данных.. Предотвращение возможности выявления конфиденциальных значений из данных, содержащихся в регулярных и стохастических БД. Контроль согласованности при использовании БД, обеспечивающий защиту и целостность отдельных элементов данных, в частности их значений. Это означает, что данные в БД всегда логически связаны и значения критических данных передаются от узла к узлу только при наличии специальных полномочий. Контекстная защита данных, состоящая в защите отдельного элемента БД в каждый данный момент времени в зависимости от поведения всей системы защиты, а также предшествующих операций, выполненных над этим элементо Защита подсистемы управления процессами в ВС. Среди большого числа различных процедур защиты подсистемы управления процессами в ВС следует выделить следующие: o обеспечение защиты ресурсов сети от воздействия неразрешенных процессов и несанкционированных запросов обеспечение целостности ресурсов при ошибочных операциях; o обеспечение защиты ресурсов сети от несанкционированного копирования или использования o обеспечение защиты при взаимодействии недружественных программных систем (процессов); o реализация программных систем, не обладающих памятью; o защита распределенных вычислений. Первые три процедуры связаны с защитой и обеспечением целостности ресурсов ВС, в то время как последние три относятся к организации вычислительных процессов в сети к реализации сетевого окружения. Концепция защищенной ВС может быть реализована только исходя из учета всего перечня функций, процедур и средств защиты, перечисленных выше по всем четырем группам защиты. Таким образом: Защищенная вычислительная сеть - это сеть в которой все операции выполняются только при соблюдении строго определенных правил и условий, или, другими словами, если все функции, процедуры и средства защиты по всем четырем группам защиты, перечисленные выше, реализованы в ВС.
Защита линий связи ВС. Линии связи - один из наиболее уязвимых компонентов ВС. В их составе можно указать большое число потенциально опасных мест, через которые злоумышленники могут проникнуть в ВС. Действия злоумышленников квалифицируются как пассивные и активные вторжения. В случае пассивного вторжения (наблюдения за сообщениями) наблюдения за управляющей информацией, проверка длины сообщений, времени отправления, частоты сеансов связи, анализ графика, нарушение защиты сеансов связи - специальной формой защиты каналов передачи является двухуровневая защита линий связи при которой реализуются следующие уровни защиты: защита процесса передачи сообщения и шифрование текста самого сообщения. Такой механизм защиты называется чистым каналом. Более жесткое требование, используемое для защиты передаваемых сообщений, состоит в том, что истинные идентификаторы объектов ВС должны быть скрыты не только от пассивных вторжений со стороны незарегистрированных пользователей, но также и друг от друга. Такое средство защиты называется цифровым псевдонимом. В этом случае пользователь получает разные идентификаторы для разных соединений, тем самым скрывая истинные идентификаторы не только от злоумышленников, но также и от равноправных партнеров. Соответствующие средства защиты ВС, необходимые для противодействия пассивным вторжениям в подсистемах связи состоят в следующем:
o защита содержания сообщения; o предотвращение возможности анализа графика; o чистый канал; o цифровой псевдоним.
Злоумышленник может организовать активные вторжения, осуществляя различные манипуляции над сообщениями во время соединения. Сообщения могут быть неявно модифицированы, уничтожены, задержаны, скопированы, изменен порядок их следования, введены в сеть через линию связи в более позднее время. Могут быть также синтезированы ложные сообщения и введены в сеть через канал связи (передачи данных). Механизмы защиты при активном вторжении существенно зависят от способов вторжения,
В августе 1977 года в колонке «Математические игры» Мартина Гарднера в журнале Scientific American, с разрешения Рональда Ривеста появилось первое описание криптосистемы RSA. В качестве открытых параметров системы были использованы числа r=1143816...6879541 (129 десятичных знаков, 425 бит, также известно как RSA-129) и a=9007. За расшифровку была обещана награда в 100 долларов США. По заявлению Ривеста, для факторизации числа потребовалось бы более 40 квадриллионов лет. Однако чуть более чем через 15 лет, 3 сентября 1993 года было объявлено о старте проекта распределѐнных вычислений с координацией через электронную почту по нахождению сомножителей числа RSA-129 и решению головоломки. На протяжении полугода более 600 добровольцев из 20 стран жертвовали процессорное время 1600 машин (две из которых были факс-машинами). В результате были найдены простые множители и расшифровано исходное сообщение, которое представляет собой фразу «THE MAGIC WORDS ARE SQUEAMISH OSSIFRAGE (англ.)» («Волшебные слова — это брезгливый ягнятник»). Полученную награду победители пожертвовали в фонд свободного программного обеспечения.
На данный момент асимметричное шифрование на основе открытого ключа RSA (расшифровывается, как Rivest, Shamir and Aldeman - создатели алгоритма) использует большинство продуктов на рынке информационной безопасности. Его криптостойкость основывается на сложности разложения на множители больших чисел, а именно - на исключительной трудности задачи определить секретный ключ на основании открытого, так как для этого потребуется решить задачу о существовании делителей целого числа. Наиболее криптостойкие системы используют 1024-битовые и большие числа. Рассмотрим алгоритм RSA с практической точки зрения. Для начала необходимо сгенерировать открытый и секретные ключи: § Возьмем два больших простых числа p and q. § Определим n, как результат умножения p on q (n= p*q). § Выберем случайное число, которое назовем d. Это число должно быть взаимно простым (не иметь ни одного общего делителя, кроме 1) с результатом умножения (p-1)*(q-1). § Определим такое число е, для которого является истинным следующее соотношение (e*d) mod ((p-1)*(q-1))=1. § Hазовем открытым ключем числа e и n, а секретным - d и n. Для того, чтобы зашифровать данные по открытому ключу {e,n}, необходимо следующее: § разбить шифруемый текст на блоки, каждый из которых может быть представлен в виде числа M(i)=0,1,2..., n-1(т.е. только до n-1). § зашифровать текст, рассматриваемый как последовательность чисел M(i) по формуле C(i)=(M(I)^e)mod n. Чтобы расшифровать эти данные, используя секретный ключ {d,n}, необходимо выполнить следующие вычисления: M(i) = (C(i)^d) mod n. В результате будет получено множество чисел M(i), которые представляют собой исходный текст.
Зашифруем и расшифруем сообщение "САВ" по алгоритму RSA. Для простоты возьмем небольшие числа - это сократит наши расчеты. § Выберем p=3 and q=11. § Определим n= 3*11=33. § Hайдем (p-1)*(q-1)=20. Следовательно, d будет равно, например, 3: (d=3). § Выберем число е по следующей формуле: (e*3) mod 20=1. Значит е будет равно, например, 7: (e=7). § Представим шифруемое сообщение как последовательность чисел в диапозоне от 0 до 32 (незабывайте, что кончается на n-1). Буква А =1, В=2, С=3. Теперь зашифруем сообщение, используя открытый ключ {7,33} C1 = (3^7) mod 33 = 2187 mod 33 = 9;
Теперь расшифруем данные, используя закрытый ключ {3,33}. M1=(9^3) mod 33 =729 mod 33 = 3(С); Данные расшифрованы!
Средства защиты информации — это совокупность инженерно-технических, электрических, электронных, оптических и других устройств и приспособлений, приборов и технических систем, а также иных вещных элементов, используемых для решения различных задач по защите информации, в том числе предупреждения утечки и обеспечения безопасности защищаемой информации. В целом средства обеспечения защиты информации в части предотвращения преднамеренных действий в зависимости от способа реализации можно разделить на группы: § Технические (аппаратные) средства. Это различные по типу устройства (механические, электромеханические, электронные и др.), которые аппаратными средствами решают задачи защиты информации. Они препятствуют доступу к информации, в том числе с помощью её маскировки. К аппаратным средствам относятся: генераторы шума, сетевые фильтры, сканирующие радиоприемники и множество других устройств, «перекрывающих» потенциальные каналы утечки информации или позволяющих их обнаружить. Преимущества технических средств связаны с их надежностью, независимостью от субъективных факторов, высокой устойчивостью к модификации. Слабые стороны — недостаточная гибкость, относительно большие объём и масса, высокая стоимость. § Программные средства включают программы для идентификации пользователей, контроля доступа, шифрования информации, удаления остаточной (рабочей) информации типа временных файлов, тестового контроля системы защиты и др. Преимущества программных средств — универсальность, гибкость, надежность, простота установки, способность к модификации и развитию. Недостатки — ограниченная функциональность сети, использование части ресурсов файл-сервера и рабочих станций, высокая чувствительность к случайным или преднамеренным изменениям, возможная зависимость от типов компьютеров (их аппаратных средств). § Смешанные аппаратно-программные средства реализуют те же функции, что аппаратные и программные средства в отдельности, и имеют промежуточные свойства. § Организационные средства складываются из организационно-технических (подготовка помещений с компьютерами, прокладка кабельной системы с учетом требований ограничения доступа к ней и др.) и организационно-правовых (национальные законодательства и правила работы, устанавливаемые руководством конкретного предприятия). Преимущества организационных средств состоят в том, что они позволяют решать множество разнородных проблем, просты в реализации, быстро реагируют на нежелательные действия в сети, имеют неограниченные возможности модификации и развития. Недостатки — высокая зависимость от субъективных факторов, в том числе от общей организации работы в конкретном подразделении. § Антивирусная программа (антивирус) — программа для обнаружения компьютерных вирусов и лечения инфицированных файлов, а также для профилактики — предотвращения заражения файлов или операционной системы вредоносным кодом.
Специфическая особенность защиты информации в компьютерных системах заключается в том, что информация не является “жёстко связанной” с носителем, а может легко и быстро копироваться и передаваться по каналам связи. Криптография исторически появилась в связи с необходимостью передачи секретной информации. Первоначально её целью являлась разработка специальных методов преобразования информации в форму недоступную для потенциального злоумышленника. С широкомасштабным применением электронных способов передачи и обработки информации задачи криптографии расширились. Современные проблемы криптографии включают разработку систем электронной цифровой подписи и тайного электронного голосования, идентификации удаленных пользователей, методов защиты от навязывания ложных сообщений и др. Шифрова́ние — обратимое преобразование информации в целях сокрытия от неавторизованных лиц, с предоставлением, в это же время, авторизованным пользователям доступа к ней. Главным образом, шифрование служит задачей соблюдения конфиденциальности передаваемой информации. Важной особенностью любого алгоритма шифрования является использование ключа, который утверждает выбор конкретного преобразования из совокупности возможных для данного алгоритма[1][2]. Пользователи являются авторизованными, если они обладают определенным аутентичным ключом. Вся сложность и, собственно, задача шифрования состоит в том, как именно реализован этот процесс[1]. В целом, шифрование состоит из двух составляющих — зашифрование и расшифрование. С помощью шифрования обеспечиваются три состояния безопасности информации[1]: · Конфиденциальность. Шифрование используется для скрытия информации от неавторизованных пользователей при передаче или при хранении. · Целостность. Шифрование используется для предотвращения изменения информации при передаче или хранении. · Идентифицируемость. Шифрование используется для аутентификации источника информации и предотвращения отказа отправителя информации от того факта, что данные были отправлены именно им.
Криптоанализ (от др.-греч. κρυπτός — скрытый и анализ) — наука о методах расшифровки зашифрованной информации без предназначенного для такой расшифровки ключа. Термин был введён американским криптографом Уильямом Ф. Фридманом в 1920 году в рамках его книги «Элементы криптоанализа». Неформально криптоанализ называют также взломом шифра. В большинстве случаев под криптоанализом понимается выяснение ключа; криптоанализ включает также методы выявления уязвимости криптографических алгоритмов или протоколов. Первоначально методы криптоанализа основывались на лингвистических закономерностях естественного текста и реализовывались с использованием только карандаша и бумаги. Со временем в криптоанализе нарастает роль чисто математических методов, для реализации которых используются специализированные криптоаналитические компьютеры. Попытку раскрытия конкретного шифра с применением методов криптоанализа называют криптографической атакой на этот шифр. Криптографическую атаку, в ходе которой раскрыть шифр удалось, называют взломом или вскрытием. При оценке стойкости алгоритма шифрования рассматривают несколько наиболее распространенных моделей криптоаналитических атак. Атака на основе только шифртекста. При выполнении этой атаки криптоаналитику доступно некоторое количество шифртекстов, являющихся результатом применения одного алгоритма шифрования. Задача криптоаналитика заключается в том, чтобы найти как можно больше открытых текстов, соответствующих имеющимся шифртекстам, а еще лучше — определить ключ, использованный при зашифровании. Входные данные для атаки на основе только шифртекста могут быть получены простым перехватом зашифрованных сообщений, что при передаче по открытым каналам связи сравнительно легко реализуемо. Данная атака является самой слабой и неудобной для криптоаналитика. Атака на основе открытого текста. При выполнении этой атаки криптоаналитик имеет доступ не только к шифртекстам, но и к соответствующим им открытым текстам. Задача криптоаналитика сводится к нахождению ключа шифрования, использованного для имеющихся пар текстов, или построению алгоритма, позволяющего расшифровывать любые сообщения, зашифрованные на этом ключе. Открытые тексты, необходимые для данной атаки, могут быть получены из разных источников. Например, если известно, что передается зашифрованный файл с определенным именем, то по расширению часто можно сделать предположение о содержимом определенных фрагментов файла, например заголовка. Данная атака сильнее, чем атака на основе только шифртекста. Атака на основе подобранного открытого текста. В данном случае в распоряжении криптоаналитика также есть некоторое число шифртекстов и соответствующих им открытых текстов. Но, кроме того, криптоаналитик имеет возможность выбрать несколько произвольных открытых текстов и получить соответствующие им шифртексты. Задача криптоаналитика точно такая же, что и при атаке на основе открытого текста: определить использованный ключ шифрования или найти иной способ расшифровывать сообщения, зашифрованные на том же ключе. Атака на основе адаптивно подобранного открытого текста. Этот вариант является расширением атаки на основе подобранного открытого текста. Отличие заключается в том, что, получив шифртекст, соответствующий выбранному открытому тексту, криптоаналитик может принять решение, какой открытый текст он хочет зашифровать в следующий раз. При поиске ключа, необходимого для расшифровки перехваченного сообщения, в распоряжении криптоаналитика всегда находится метод полного перебора ключевого пространства. Поэтому объем ключевого пространства, используемого в криптосистеме, должен быть настолько велик, чтобы в ближайшем будущем полный перебор не успел бы завершиться.
9 вопрос
Сравнения Если два числа a и b (a, b ∈ Z) при делении на число m (m ∈ N) дают один и тот же остаток r, где, то числа a и b называются сравнимыми по модулю m. Сравнимость чисел a и b по модулю m принято записывать так: a b (mod m), и читать: a сравнимо с b по модулю m. Если a b (mod m), то 1) a = b + mt, где t ∈ Z. 2) Разность a - b делится на m
Свойства сравнения 1. Если a b (mod m) и a c (mod m), то b c (mod m); a, b, c Z, m ∈ N. 2. Если a 1 b 1(mod m), a 2 b 2(mod m),..., a n b n(mod m), то a 1 + a 2 +... + a n b 1 + b 2 +... + b n(mod m); a i, b i ∈ Z, m, n ∈ N. 3. Если a 1 b 1(mod m), a 2 b 2(mod m),..., a n b n(mod m), то a 1 · a 2 ·... · a n b 1 · b 2 ·... · b n(mod m); a i, b i ∈ Z, m, n ∈ N. 4. Если a b (mod m), то an bn (mod m); a, b ∈ Z, m, n ∈ N. 5. Если a b (mod m), то ak bk (mod m); a, b, k ∈ Z, m, n ∈ N. 6. Если a b (mod m), и a, и m делятся на k, то и b делится на k; a, b, k ∈ Z, m, n ∈ N. Признак делимости на 2. Целое число делится на 2 тогда и только тогда, когда последняя его цифра делится на 2 (т.е. число четное). Например, 288 делится на 2, т.к. 8 делится на 2. Признак делимости на 3. Целое число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3. Например, 462 делится на 3, т.к. 4 + 6 + 2 = 12 делится на 3. Признак делимости на 4. Целое число делится на 4 тогда и только тогда, когда число, образованное последними двумя цифрами делится на 4. Например, 1352 делится на 4, т.к. 52 делится на 4. Признак делимости на 5. Целое число делится на 5 тогда и только тогда, когда последняя цифра числа делится на 5 (т.е. число оканчивается на 5 или на 0). Например, 235 делится на 5, т.к. 5 делится на 5. Признак делимости на 6. Целое число делится на 6 тогда и только тогда, когда оно одновременно делится на 2 и на 3 (т.е. число четное и сумма цифр числа делится на 3). Например, 4602 делится на 6, т.к. 4602 - парное и 4 + 6 + 0 + 2 = 12 делится на 3. Признак делимости на 8. Целое число делится на 8 тогда и только тогда, когда число, образованное последними тремя цифрами делится на 8. Например, 32168 делится на 8, т.к. 168 делится на 8. Признак делимости на 9. Целое число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9. Например, 756 делится на 3, т.к. 7 + 5 + 6 = 18 делится на 9. Признак делимости на 10. Целое число делится на 10 тогда и только тогда, когда число оканчивается на 0. Например, 2030 делится на 10, т.к. оканчивается на 0. Признак делимости на 11. Целое число делится на 11 тогда и только тогда, когда разница суммы цифр, стоящих на непарных местах, и суммы цифр стоящих на парных местах числа делится на 11.
очень много для помехоустойчивого кодирования сделал Ричард Хэмминг. В частности, он разработал код, который обеспечивает обнаружение и исправление одиночных ошибок при минимально возможном числе дополнительных проверочных бит. Для каждого числа проверочных символов используется специальная маркировка вида (k, i), где k — количество символов в сообщении, i — количество информационных символов в сообщении. Например, существуют коды (7, 4), (15, 11), (31, 26). Каждый проверочный символ в коде Хэмминга представляет сумму по модулю 2 некоторой подпоследовательности данных. Рассмотрим сразу на примере, когда количество информационных бит i в блоке равно 4 — это код (7,4), количество проверочных символов равно 3. Классически, эти символы располагаются на позициях, равных степеням двойки в порядке возрастания: первый проверочный бит на 20 = 1; r1 = i1 + i2 + i4 r1 r2 i1 r3 i2 i3 i4 e0,e1,e2 опрделяются как функции, зависящие от принятых декодером бит k1 — k7:
e0 = k1 + k3 + k5 + k7 mod 2
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.1.38 (0.017 с.) |


 (1)
где М — k -разрядное двоичное число;
(1)
где М — k -разрядное двоичное число;  операция добавления избыточного n -разрядного поля в конце числа М, (k>п); G — (n +1)-разрядное двоичное число, делитель выражения (1); Q — целая часть частного от деления
операция добавления избыточного n -разрядного поля в конце числа М, (k>п); G — (n +1)-разрядное двоичное число, делитель выражения (1); Q — целая часть частного от деления  ; R - остаток от деления
; R - остаток от деления  .
Пусть передаче подлежит кадр (цикл) данных размером k бит. Добавим в конце кадра избыточное поле (называемое КПК-комбинацией проверки кадра) размером п, заполненное нулями. Данная операция равносильна умножению на 2 n. Полученный избыточный кадр разделим на другое двоичное число, называемое порождающим полиномом, содержащее на один разряд больше (n + 1), чем КПК. Операция деления эквивалентна операции исключающего ИЛИ, выполняемой параллельно над парами битов по мере обработки каждого бита кадра (рис.1). Результатом деления
.
Пусть передаче подлежит кадр (цикл) данных размером k бит. Добавим в конце кадра избыточное поле (называемое КПК-комбинацией проверки кадра) размером п, заполненное нулями. Данная операция равносильна умножению на 2 n. Полученный избыточный кадр разделим на другое двоичное число, называемое порождающим полиномом, содержащее на один разряд больше (n + 1), чем КПК. Операция деления эквивалентна операции исключающего ИЛИ, выполняемой параллельно над парами битов по мере обработки каждого бита кадра (рис.1). Результатом деления  являются целая часть и остаток R. Целая часть игнорируется, а остаток записывается на избыточное поле. Кадр передаётся по линии связи.
являются целая часть и остаток R. Целая часть игнорируется, а остаток записывается на избыточное поле. Кадр передаётся по линии связи.
 Рис. 1. Пример кодирования в процедуре CRC
Рис. 2 и 3 иллюстрируют процедуру CRC-4, применённую к 8-битовому кадру 11100110. Порождающий полином (x 4+ x 3+1), что соответствует двоичной комбинации коэффициентов порождающего полинома, равной 11001. В приемнике вся полученная последовательность битов делится на тот же порождающий полином, который был применен в передатчике. Возможны два случая (рис. 2).
В первом ошибок в сообщении нет и поэтому получаемый остаток равен нулю. Во втором примере в конце переданной последовательности битов имеется пачка ошибок длиной 4 бита. Поэтому остаток от деления R не равен нулю, что свидетельствует о наличии ошибок. Последовательность операций процедуры показана на рис. 3.
Рис. 1. Пример кодирования в процедуре CRC
Рис. 2 и 3 иллюстрируют процедуру CRC-4, применённую к 8-битовому кадру 11100110. Порождающий полином (x 4+ x 3+1), что соответствует двоичной комбинации коэффициентов порождающего полинома, равной 11001. В приемнике вся полученная последовательность битов делится на тот же порождающий полином, который был применен в передатчике. Возможны два случая (рис. 2).
В первом ошибок в сообщении нет и поэтому получаемый остаток равен нулю. Во втором примере в конце переданной последовательности битов имеется пачка ошибок длиной 4 бита. Поэтому остаток от деления R не равен нулю, что свидетельствует о наличии ошибок. Последовательность операций процедуры показана на рис. 3.
 Рис. 2. Пример декодирования в процедуре CRC
Рис. 2. Пример декодирования в процедуре CRC
 Рис. 3. Алгоритм процедуры CRC
Рис. 3. Алгоритм процедуры CRC





