
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Площадь криволинейной трапеции.Стр 1 из 3Следующая ⇒
Определённый интеграл. Площадь криволинейной трапеции. Т.: Если ф-ция f(x)³0 непрерывна на отр. [a,b], то предел Определение определённого интеграла. !!!Т.: Если ф-ция f(x) непрерывна на отр. [a,b], то сущ. интеграл: 1.2. Св-ва определённого интеграла:
Т.: При любых (a, b, c) верна ф-ла: Формула Ньютона – Леиблица. Т.: Если f(x) непрерывна на отр. [a,b], то !!!Т. (ф-ла Н.-Ле.): Если f(x) непрерывна на отр. [a,b], то верна ф-ла: Замена переменной. Т.1: Если 1) f(x) непрерывна на отр. [a,b] 2) x=j(t) [a,b] Û [a,b] 3) j’(t) непрерывна [a,b] 4) j(a)=a, j(b)=b;
Интегрирование по частям. Т.2: Если u(x) и v(x) непрерывна на отр. [a,b]: dv=v’dx, du=u’dx Не собственные интегралы.
2. Задача f(x) [a,+¥) $ 3. 4. 5. 6. 7. f(x) [a,b], f(x) не огр. b $ 8. Площадь фигуры. Криволинейный сектор. F(x)³0 непр. [a,b] Þ
Длина кривой.
Метод параллельных сечений.
Площадь поверхности вращения.
Функций нескольких переменных. Определение ф-ций. Опр.1: Переменная “z” называется ф-цией от переменной “x” и “y” с областями изменения X и Y, если иметься правило что каждой паре (“x” и “y”) “x Î X ” и “y Î Y”, ставиться в соответствие одно значение “z Î Z” Þ z=f(x,y), способ задания: табличный, формульный, графический. Предел и непрерывность функций. Опр.1: Число а называется приделом ф-ций f(x,y) в т. (x0,y0), если по любому наперёд заданному e>0 найдётся проколотая d окрестность -Ud(x0,y0) что для всех (x,y) выполняется неравенство: |f(x,y)-a|<e Свойство: 1) 3) Опр.3: f(x, y) называется непрерывной в т. (x0,y0) если её полное приращение в этой точке есть бесконечно малое при бесконечно малых приращениях Dx и Dy:
Частные производные.
Полный дифференциал:
Опр.: f(x, y) называется дифференциалом в т. М(x, y), если в этой т. выполняется равенство (1). Т.(дост.усл.): частные производные Производные сложней ф-ций.
Дифференциал неявной ф-ций.
Дифференциал неявной ф-ций (3-ёх переменных).
Производные и дифференциалы высших порядков. Производные.
Дифференциалы. d2z=d(dz) d3z=d(d2z) dnz=d(dn-1z) Формула Теилара.
Локальные экстремумы. Т.(необ.усл.): Если f(x) имеет в т. x0 локальные экстремум, то в этой точке f’(x)=0 или не сущ. Опр.: Ф-ция f(x,y) имеет в т. M0(x0,y0) лок. Макс. (Мин.) если найдется окрестность в т. М0 такая в которой выполняется неравенство: Т.(необ.усл.): Если ф-ция f(x,y) имеет в т. M0(x0,y0) лок. экстремумы, то в этой т. част. производная
Т.2.(дост. усл.): Пусть М0(0,0) стационарна для f(x,y), Если в М0:
Т.3.: Если в Глобальные экстремумы. Y=f(x) [a,b] Схема: 1) лок. экстремумы в (a,b) 2) f(a) и f(b) 3) выбрать Z=f(x,y) в области Е наибольшее и наименьшее Y=f(x) в Е: Схема: 1) найти лок. экстре. внутри Е 2) Найти наибольшее и наименьшее на гранитсе g 3) Выбрать Градиент.
Опр.: Вектор, компонентами которого служат значения частных производных Т.: направление градиента в заданной точке есть направление, в котором ф-ция возрастает с наибольшей скоростью:
Вычисление интеграла. Т.: 1) сущ. 2) сущ.
Замена переменной. Условия: 1) (*) устано. взаимное соответствие D«D’ 2) j, y, 3) 4) f(x,y) непр. D Т.1.: Если выполнимы условия 1-4, то верна:
Т.2.: Приложение двойного интеграла.
Механическое приложение.
Т.: Любая не прерывная в области V f(x,y,z) интегрируема в этой области. Свойства: 1) 2) Замена переменной.
Условия: 1) (*) установим взаимно однозначное соответствие V«V’ 2) 3) 4) f(x,y,z) непре. V Т.: Если выполняется условие 1-4 то верна формула:
Приложение тройного интеграла.
Механическое приложение.
Криволинейные интегралы. Определение и св-во.
Приложение криволинейных интегралов. Площадь фигуры.
Работа силы.
Ряды. Числовой ряд и его сумма.
Сходимость / рас ходимость ряда:
Т.: Поведение сходимости / рас ходимости ряда не меняется, если:
Теорема сравнения. Т.: Если ak£bk "k, то:
Признаки Даламбера и Коши. Пр. Даламбера только для положительных рядов. Т.1(Пр. Даламбера): Если существует
Т.2(Пр. Коши): Если существует
5.5. Интегральный признак Коши. Признак - Т.(необх. пр. Коши): Если найдётся непрерывная не возрастающая функция j(x) на [1,+¥] такая, что j(n)=an "n (an>0), то
5.6. Знакочередующиеся ряды.
Т.(пр. Лейбнеца): 1) 2) an³an+1 "n члены не возрастают, то (*) сходиться.
5.7. Абсолютная и условная сходимость ряда. Т.1: Если исходный ряд расходиться, ряд составленный из модулей членов этого ряда не может сходиться. Т.2: Если сходиться ряд составленный из модулей членов исходного ряда, то сходиться и исходный ряд. Т.3: Абсолютно сходящиеся ряды обладают свойствами коммутативности и ассоциативности Условно сходящиеся ряды этим свойством не обладают. Т.4 (Риман): Если условно ряд сходиться, то для "s (в том числе -¥ и +¥) можно указать перестановку членов ряда такую что преобразованный ряд сходиться к числу s или расходиться к -¥ или +¥. Т.5: Перестановка членов абсолютно сходящегося ряда не меняет его суммы. Абсолютная сходимость – если сходиться ряд составленный из абсолютных величин его членов. Условная сходимость – если знакопеременный ряд сходиться, а ряд составленный из абсолютных его величин расходиться. 5.8. Функциональные ряды. Опр.:
Степенной ряд. Опр.: Т.1(Абель): Если степенной ряд сходиться в точке x0 (x0¹0), то он абсолютно сходиться для всех x, удовлетворяющих условию |x|<|x0|. Если степенной ряд расходиться в точке x’0 (x’0¹0), то он абсолютно расходиться для всех x, удовлетворяющих условию |x|>|x’0|. Свойство степенных рядов. Т.1: Внутри интервала сходимости ( - R, R) сумма степенного ряда s(x) есть ф-ция непр. Т.2: Внутри интервала сходимости ( - R, R) сумма степенного ряда s(x) диффер. и интегрируема и находиться соответственно n-членным дифференциалом или интегрированием.
Ряды Тейлора и Маклорена. Т.: Сумма степенного ряда s(x), связана с коэффициентами степенного ряда с помощью формулы (**)
Биномный ряд.
Приложение: Опр.(def Lim):
Определённый интеграл. Площадь криволинейной трапеции. Т.: Если ф-ция f(x)³0 непрерывна на отр. [a,b], то предел
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.160.216 (0.093 с.) |
 всегда сущ:
всегда сущ: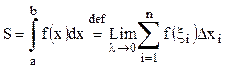



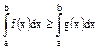
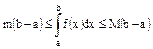

 если суш-ет два из этих интегралов.
если суш-ет два из этих интегралов.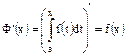


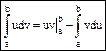
 Задача y=1/(1+x2)
Задача y=1/(1+x2) 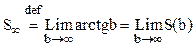


 Задача f(x) [-¥,b) $
Задача f(x) [-¥,b) $ 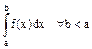




 Т.: Если f(x) интегрирована на отр. [a,b], то она иррациональна на этом отр. [a,b]:
Т.: Если f(x) интегрирована на отр. [a,b], то она иррациональна на этом отр. [a,b]: 
 f(x) [a,b], f(x) не огр. а $
f(x) [a,b], f(x) не огр. а $ 
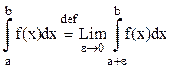
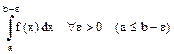



 F(x)£0 непр. [a,b] Þ
F(x)£0 непр. [a,b] Þ 





 - S криволинейного сектора.
- S криволинейного сектора.
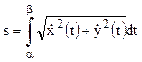



 - Объём тела по площади || сечения.
- Объём тела по площади || сечения. - Объём тела вращения.
- Объём тела вращения.
 2)
2) 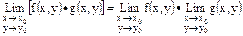
 4)
4) 


 - частное приращения по x.
- частное приращения по x. - частное приращения по y.
- частное приращения по y. - частная производная f(x,y) по x.
- частная производная f(x,y) по x. - частная производная f(x,y) по y.
- частная производная f(x,y) по y.
 - частная производная f(x,y,z) по x.
- частная производная f(x,y,z) по x.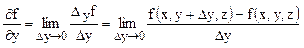 - частная производная f(x,y,z) по y.
- частная производная f(x,y,z) по y. - частная производная f(x,y,z) по z.
- частная производная f(x,y,z) по z. 2.4. Дифференциал.
2.4. Дифференциал. -17 вопрос
-17 вопрос - полное приращение функций.
- полное приращение функций.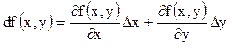



 если эти непрерывны в окр. М(x, y)то верна формула (1).
если эти непрерывны в окр. М(x, y)то верна формула (1).



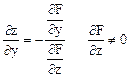


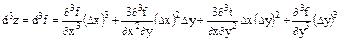



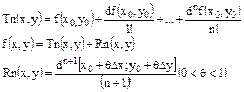


 или 0 или не существует.
или 0 или не существует.

 имеет локальный экстремум, то в этой точке частные производные
имеет локальный экстремум, то в этой точке частные производные  равны 0 или не сущ-ют.
равны 0 или не сущ-ют.
 .
. - 21 вопрос.
- 21 вопрос.
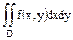
 , то верна
, то верна  ;
;

 непр. D’
непр. D’ - Функциональный определитель.
- Функциональный определитель.
 - Переход к целиндр. коорд.
- Переход к целиндр. коорд.
 - Плотность вещества.
- Плотность вещества. - Момент инерций площади плоской фигуры. g(x,y) – плотность.
- Момент инерций площади плоской фигуры. g(x,y) – плотность. - Координаты центра тяжести площади плоской фигуры.
- Координаты центра тяжести площади плоской фигуры. 3.6. Тройной интеграл.
3.6. Тройной интеграл. 






 -Масса тела.
-Масса тела. -Момент инерций тела [g(x,y,z) – масса тела]
-Момент инерций тела [g(x,y,z) – масса тела] - Координаты центра тяжести тела [g(x,y,z) – плотность в-ва.]
- Координаты центра тяжести тела [g(x,y,z) – плотность в-ва.]


 - числовой ряд (бесконечная последовательность чисел).
- числовой ряд (бесконечная последовательность чисел). - гармонический ряд.
- гармонический ряд.  - геометрический ряд.
- геометрический ряд. - частичная сумма.
- частичная сумма. - для гармонического ряда.
- для гармонического ряда. - для геометрического ряда.
- для геометрического ряда.


 , то
, то

 , то
, то
 одновременно или сходятся или расходятся.
одновременно или сходятся или расходятся.



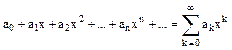





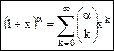



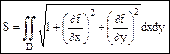 -S куска поверхности.
-S куска поверхности. 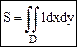 - S плоской области.
- S плоской области. - сфера
- сфера  - цилиндр
- цилиндр  - парабфлойд
- парабфлойд - 3-остный элипсойд
- 3-остный элипсойд  - 1 – остный гипербалойд
- 1 – остный гипербалойд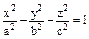 - 2–остный гипербалойд
- 2–остный гипербалойд  - конус
- конус


