Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
FIGURE 46.1 State variable compensator employing full-state feedback in series with a full-state observer.Содержание книги
Поиск на нашем сайте
A key question that arises in the design of state variable compensators is whether or not all the poles of the closed-loop system can be arbitrarily placed in the complex plane. Recall that the poles of the closed-loop system are equivalent to the eigenvalues of the system matrix in state variable format. As we shall see, if the system is controllable and observable, then we can accomplish the design objective of placing the poles precisely at the desired locations to meet the performance specifications. Full-state feedback design commonly relies on pole-placement techniques. It is important to note that a system must be completely controllable and completely observable to allow the flexibility to place all the closed-loop system poles arbitrarily.
Full state feedback (FSF), or pole placement, is a method employed in feedback control system theory to place the closed-loop poles of a plant in pre-determined locations in the s-plane. Placing poles is desirable because the location of the poles corresponds directly to the eigenvalues of the system, which control the characteristics of the response of the system. The system must be considered controllable in order to implement this method.
If the closed-loop input-output transfer function can be represented by a state space equation, see State space (controls),
then the poles of the system are the roots of the characteristic equation given by
Full state feedback is utilized by commanding the input vector
Substituting into the state space equations above,
The roots of the FSF system are given by the characteristic equation, Example 46.1 Consider a control system given by the following state space equations
The uncontrolled system has closed-loop poles at s = − 1 and s = − 2. Suppose, for considerations of the response, we wish the controlled system eigenvalues to be located at s = − 1 and s = − 5. The desired characteristic equation is then s 2 + 6 s + 5 = 0. Following the procedure given above,
Upon setting this characteristic equation equal to the desired characteristic equation, we find
Therefore, setting
Determining the gain matrix K is the objective of the full-state feedback design procedure. The beauty of the state variable design process is that the problem naturally separates into a full-state feedback component and an observer design component. These two design procedures can occur independently, and in fact, the separation principle provides the proof that this approach is optimal. We will show later that the stability of the closed-loop system is guaranteed if the full-state feedback control law stabilizes the system (under the assumption of access to the complete state) and the observer is stable (the tracking error is asymptotically stable). Observer design will be discussed in Lecture 4.7.
Example 46.2 Let’s consider a 3rd order control system which is described by the following differential equation
We may choose the following state variables
Then we may describe this system in matrix form
and
If the state variable feedback matrix is
and
then the closed-loop system is
The state feedback matrix is
and the characteristic equation is
If we seek a rapid response with a low overshoot, we choose a desired characteristic equation such as (see Equation 5.18 and Table 5.2)
We choose If we want a settling time (with a 2% criterion) equal to 1 second, then
If we choose
Comparing Equations (46.1) and (46.2) yields the three equations
Therefore, we require that
Example 46.3 Let’s consider a control system with full-state feedback control (output variable This system is using a DC motor which is controlled by an exciting circuit. The transfer function of this DC motor is as follows
where We suppose that As you may see from Fig.46.2 the control system has 3 feedback loops: on position, motor speed, and excitation current. Suppose, that the coefficient of feedback loop on position is equal to -1 (look at Fig.46.3).
Fig.46.2 A control system with full-state feedback control (output variable
|
||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.35.234 (0.008 с.) |




 . Consider an input proportional (in the matrix sense) to the state vector,
. Consider an input proportional (in the matrix sense) to the state vector, .
.
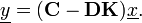
 . Comparing the terms of this equation with those of the desired characteristic equation yields the values of the feedback matrix
. Comparing the terms of this equation with those of the desired characteristic equation yields the values of the feedback matrix  which force the closed-loop eigenvalues to the pole locations specified by the desired characteristic equation.
which force the closed-loop eigenvalues to the pole locations specified by the desired characteristic equation.
 , and the FSF controlled system characteristic equation is
, and the FSF controlled system characteristic equation is .
. .
.







 (46.1)
(46.1)
 = 0.8 for minimal overshoot and
= 0.8 for minimal overshoot and  to meet the settling time requirement.
to meet the settling time requirement.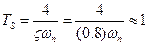
 (46.2)
(46.2)


 = 9.4,
= 9.4,  = 79.1, and
= 79.1, and  =170.8. The step response has no overshoot and a settling time of 1 second, as desired.
=170.8. The step response has no overshoot and a settling time of 1 second, as desired. ).
).
 = the complex transfer coefficient of the DC motor.
= the complex transfer coefficient of the DC motor.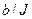 =1 and
=1 and  =5.
=5.