
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение показателей надежностиСодержание книги
Поиск на нашем сайте
Статистические исследования надежности различных типов приборов, датчиков и их элементов показывают, что время наступления внезапного отказа является величиной случайной. Поэтому при расчете приборов и датчиков пользуются вероятностными показателями надежности. Одним из основных показателей, используемых при расчетах надежности, служит вероятность внезапного отказа Qв(t)- Смысл этого понятия иллюстрируется следующим гипотетическим экспериментом. Допустим, в эксплуатации находится партия однотипных приборов в количестве N0. При определенных условиях эксплуатации определяются погрешности всех приборов через малые равные промежутки δt и регистрируются все случаи внезапных отказов. За начало отсчета времени (t=0) принимается начало эксплуатации каждого прибора. К моменту времени t часть приборов откажет и останется Nt исправных приборов. Относительное число отказавших за время t приборов будет равно
Если увеличивать N0, то в пределе, при, относительное число внезапно отказавших приборов и будет определять вероятность внезапного отказа:
С течением времени количество исправных приборов Nt, находящихся в эксплуатации, уменьшается, следовательно, вероятность отказа Qв(t) увеличивается (рис.). Скорость увеличения Qв(t) характеризуется плотностью вероятности отказов:
Наряду с понятием вероятности внезапного отказа Qв(t) пользуются вероятностью безотказной работы Pв(t), под которой понимают вероятность того, что в определенных условиях эксплуатации, в пределах заданной продолжительности t работы прибора (датчика), внезапный отказ не наступает. Статистически PB(t) определяется как предел отношения числа исправных приборов Nt к общему числу испытуемых приборов при:
С течением времени Рв(t) уменьшается (см рис.). Вероятности Qв(t) и Рв(t) связаны между собой зависимостью Qв(t)+ Рв(t)=1 (4) Из выражения (4) с учётом уравнения (3) следует, что скорость изменения вероятности безотказной работы равна плотности вероятности, взятой с обратным знаком
Следующим важным показателем надежности является интенсивность внезапных отказов λ(t). Статистически интенсивность внезапных отказов определяется отношением числа δN внезапно отказавших приборов за малый промежуток времени δt к величине этого промежутка и к числу приборов Nt, не имеющих внезапных отказов к началу расcматриваемого промежутка времени. Выражение для интенсивности внезапных отказов имеет вид:
здесь f(t) - плотность вероятности внезапных отказов, Pв(t) - вероятность безотказной работы. Если в выражении (6) заменить согласно (5)
то
Интегрируя обе части выражения (7) в пределах от 0 до t и учитывая, что Pв(0)=1, находим
Откуда
Следующий показатель это средняя наработка до отказа. Он может быть определён как математическое ожидание времени отказа:
Заменяя
получим
После интегрирования по частям определяем
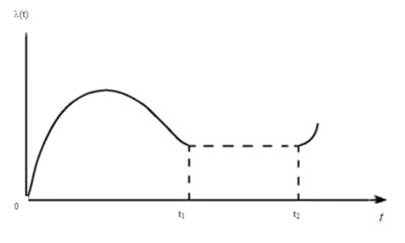
Следовательно, средняя наработка до отказа равна площади, ограниченной кривой вероятности безотказной работы и осью абсцисс (см. предыдущий рис.). Средняя наработка до отказа tcр функционально связана с интенсивностью внезапных отказов λ(t). Типичная зависимость λ от времени показана на рис. На начальном отрезке времени от 0 до t1 обычно имеет место участок приработки, во время которого отказывают дефектные элементы, в связи с чем интенсивность внезапных отказов сравнительно высока; затем интенсивность внезапных отказов уменьшается и сохраняет примерно постоянную величину на отрезке времени от t1 до t2; при t>t2 начинается период повышенной интенсивности отказов из-за выработки элементами своего ресурса. Таким образом, при средней вероятности отказа элементов технологический процесс следует строить таким образом, чтобы все элементы, входящие в приборы и датчики, проходили период приработки на заводе-изготовителе до выпуска их в эксплуатацию, при этом гарантийный срок службы таких приборов и датчиков не должен превышает интервала нормальной работы: tгар2-t1. Это позволяет при расчетах надежности приборов и датчиков считать λ(t) =const = λ. Такой частью технологического процесса, позволяющей приработать детали и элементы изделия на заводе является прогон. Однако в случае использования элементов с высокой надёжностью и обеспечения необходимого количества контрольных операций при сборке прогон изделий не требуется. Так японские и иные импортные телевизоры прогон не проходят.
На основании формул (4), (8) и (9) нетрудно получить зависимости связывающие Qв(t), Pв(t) и tср при λ(t)=const=λ:
Разлагая Pв(t) в ряд получим
Если λt<<1, то приближённо
Формулы (10) и (11) характеризуют экспоненциальный закон распределения плотности вероятности внезапных отказов. Плотность вероятности согласно (6) равна
Следовательно, при λ(t)=λ плотность вероятности f(t) так же как и вероятность Pв(t), изменяется по экспоненциальному закону: На практике встречаются и другие законы распределения плотности вероятности, но наиболее типичным является экспоненциальный закон
именно в связи с этим указанный закон положен в основу общепринятой методики расчёта вероятности внезапных отказов. Поэтому расчёт вероятности внезапных отказов и вероятности безотказной работы производят по формулам (10) и (11).
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.40.151 (0.007 с.) |



 (3)
(3)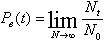

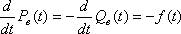 (5)
(5) (6)
(6)
 (7)
(7)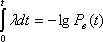
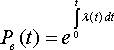 (8)
(8)
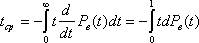
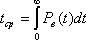 (9)
(9)
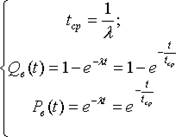 (10)
(10)
 (11)
(11)




