Основные алгоритмические конструкиии

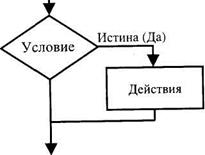
Элементарные шаги алгоритма можно объединить в следующие алгоритмические конструкции: линейные (последовательные), разветвляющиеся, циклические и рекурсивные.

Линейная алгоритмическая конструкция

Линейной называют алгоритмическую конструкцию, реализованную в виде последовательности действий (шагов), в которой каждое действие (шаг) алгоритма выполняется ровно один раз, причем после каждого i -го действия (шага) выполняется (i+1) -е действие (шаг), если i -е действие – не конец алгоритма.

Разветвляющаяся алгоритмическая конструкция

Разветвляющейся (или ветвящейся) называется алгоритмическая конструкция, обеспечивающая выбор между двумя альтернативами в зависимости от значения входных данных. При каждом конкретном наборе входных данных разветвляющийся алгоритм сводится к линейному. Различают неполное (если – то) и полное (если – то – иначе) ветвления. Полное ветвление позволяет организовать две ветви в алгоритме (то или иначе), каждая из которых ведет к общей точке их слияния, так что выполнение алгоритма продолжается независимо от того, какой путь был выбран (рис. 6.2). Неполное ветвление предполагает наличие некоторых действий алгоритма только

 

Действия 2

L

Ложь (Нет) / \^ Истина (Да)

Условие

 

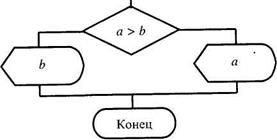
Действия 1

_Г

Рис. 6.2. Полное ветвление

на одной ветви (то), вторая ветвь отсутствует, т.е. для одного из ре­зультатов проверки никаких действий выполнять не надо, управле­ние сразу переходит к точке слияния (рис. 6.3).

Пример 6.2.

Вывести значение наибольшего из двух чисел. Псевдокод:

1. Ввод двух чисел а, Ь.

2. ЕСЛИ а > Ъ, ТО «выводим а»,

ИНАЧЕ «выводим Ь».

3. Конец.

297

Ложь (Нет)

Рис. 6.3. Неполное ветвление

( Начало J

I

/Ввод /

/ «■* /

Нет

Да

Рис. 6.4. Блок-схема к примеру 6.2

В данном примере реализовано полное ветвление. ЕСЛИ значе­ния входных данных таковы, что а > Ь, ТО выполняется линейный алгоритм:

1. Ввод двух чисел а, Ь.

2. Вывод а.

ИНАЧЕ, когда а <Ь, выполняется линейный алгоритм:

1. Ввод двух чисел а, Ь.

2. Вывод Ь.

Вывод: алгоритм является разветвляющимся и состоит из двух ветвей.

Рассмотрим стандартный алгоритм поиска наибольшего (наименьшего) значения среди не­скольких заданных. Основная идея алгоритма сводится к следу­ющему: за наибольшее (наимень­шее) принимаем значение лю­бого из данных. Поочередно сравниваем оставшиеся данные с наибольшим (наименьшим). Если окажется, что очередное значение входного данного боль­ше (меньше) наибольшего (наи­меньшего), то наибольшему (наименьшему) присваиваем это значение. Таким образом, срав­нив все входные данные, найдем наибольшее (наименьшее) среди них. Алгоритм использует непол­ное ветвление.

Пример 6.3.

Заданы три числа. Найти значение наименьшего из них.

Заданные числа обозначим: а, Ь, с; результирующее наимень­шее — тт. На рис. 6.5 представ­лена блок-схема алгоритма реше- р_Ис. 6.5. Алгоритм поиска ния данной задачи. наименьшего значения

среди трех заданных

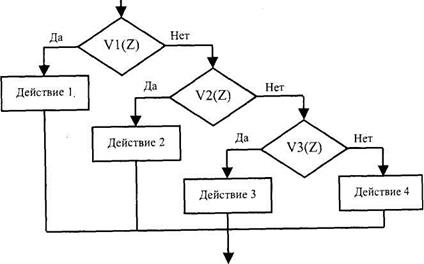
КолланЭа «Выбор»

Часто при выборе одного из возможных вариантов действий при­ходится проверять значение выражения на принадлежность заданно­му набору данных. Для этого существует команда «Выбор». При ее исполнении сначала вычисляется значение некоторого выражения Z. Затем последовательно проверяются условия VI, V2,..., V«относи­тельно Z, начиная с первого, до тех пор, пока не встретится усло­вие, принимающее значение ИСТИНА. Далее выполняется соответ­ствующее этому условию действие (или серия действий), после чего команда выбора завершается. Если ни одно из условий не является истинным, то выполняется действие (или набор действий), идущее по ветви ЛОЖЬ для каждого из условий. На рис. 6.6 представлена блок-схема команды «Выбор» для п = 3.

Правило изменения параметра и i = TV, К, h означает
1-й шаг цикла	/ = N
2-й шаг цикла	/ = N + h
3-й шаг цикла и т.д.	/ = N + 2h
последний шаг	г = К

Рис. 6.6. Команда «выбор»