
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача составления рациона (задача о диете, задача о смесях)
Имеется два вида корма I и II, содержащие питательные вещества (витамины) Таблица 2
Стоимость 1 кг корма I и II соответственно равна 4 и 6 руб. Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных, веществ было бы не менее установленного предела. Решение. Составим экономико-математическую модель задачи. Обозначим
Кроме того, переменные
Общая стоимость рациона составит (в руб.)
Итак, экономико-математическая модель задачи: составить дневной рацион Для формулировки задачи в общей постановке обозначим:
найти такой рацион
и условию
при котором функция
принимает максимальное значение. 3. Задача об использовании мощностей (задача о загрузке оборудования) Предприятию задан план производства продукции по времени и номенклатуре: требуется за время Т выпустить Необходимо составить такой план работы станков (т.е. так распределить выпуск продукции между станками), чтобы затраты на производство всей продукции были минимальными.
Составим экономико-математическую модель задачи. Обозначим Так как время работы каждого станка ограничено и не превышает Т, то справедливы неравенства:
Для выполнения плана выпуска по номенклатуре необходимо, чтобы выполнялись следующие равенства:
Кроме того,
Затраты на производство всей продукции выразятся функцией
Экономико-математическая модель задачи об использовании мощностей примет вид: найти такое решение Задача о раскрое материалов На раскрой (распил, обработку) поступает материал одного образца в количестве, а единиц. Требуется изготовить из него l разных комплектующих изделий в количествах, пропорциональных числам Необходимо найти план раскроя, обеспечивающий максимальное число комплектов. Составим экономико-математическую модель задачи. Обозначим Так как общее количество материала равно сумме его единиц, раскраиваемых различными способами, то
Требование комплектности выразится уравнениями
Очевидно, что
Экономико-математическая модель задачи: найти такое решение Для изготовления брусьев длиной 1,2 м, 3 м и 5 м в соотношении 2:1:3 на распил поступают 195 бревен длиной 6 м. Определить план распила, обеспечивающий максимальное число комплектов. Составить экономико-математическую модель задачи. Решение. Прежде всего, определим всевозможные способы распила бревен, указав соответствующее число получаемых при этом брусьев (табл. 3).
Таблица 3
Обозначим: Учитывая, что все бревна должны быть распилены, а число брусьев каждого размера должно удовлетворять условию комплектности, экономико-математическая модель задачи примет вид:
при ограничениях:
Задачу о раскрое легко обобщить на случай т раскраиваемых материалов. Пусть каждая единица j-го материала ( Обозначим Экономико-математическая модель задачи о раскрое в общей постановке примет вид: найти такое решение
и условию
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.193.172 (0.014 с.) |
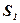 ,
,  , и
, и  . Содержание числа единиц питательных веществ в 1 кг каждого вида корма и необходимый минимум питательных веществ приведены в табл. 2 (цифры условные).
. Содержание числа единиц питательных веществ в 1 кг каждого вида корма и необходимый минимум питательных веществ приведены в табл. 2 (цифры условные). и
и  — количество кормов I и II, входящих в дневной рацион. Тогда этот рацион (см. табл. 2) будет включать (
— количество кормов I и II, входящих в дневной рацион. Тогда этот рацион (см. табл. 2) будет включать (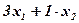 ) единиц питательного вещества
) единиц питательного вещества 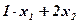 ) единиц вещества
) единиц вещества 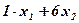 ) единиц питательного вещества
) единиц питательного вещества 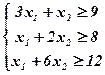 (7)
(7) ,
,  (8)
(8)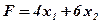 (9)
(9) , удовлетворяющий системе (7) и условию (8), при котором функция (9) принимает минимальное значение.
, удовлетворяющий системе (7) и условию (8), при котором функция (9) принимает минимальное значение. (
(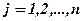 ) — число единиц корма п-го вида;
) — число единиц корма п-го вида;  (
(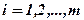 ), — необходимый минимум содержания в рационе питательного вещества
), — необходимый минимум содержания в рационе питательного вещества  ;
;  — число единиц питательного вещества
— число единиц питательного вещества  , — стоимость единицы корма j-го вида. Тогда экономико-математическая модель задачи примет вид:
, — стоимость единицы корма j-го вида. Тогда экономико-математическая модель задачи примет вид: , удовлетворяющий системе
, удовлетворяющий системе (10)
(10) , (11)
, (11) (12)
(12)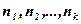 единиц продукции
единиц продукции 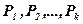 . Продукция производится на станках
. Продукция производится на станках 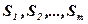 . Для каждого станка известны производительность
. Для каждого станка известны производительность  , которое можно произвести на станке
, которое можно произвести на станке 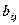 на изготовление продукции
на изготовление продукции  — время, в течение которого станок
— время, в течение которого станок 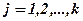 ).
).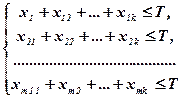 (13)
(13)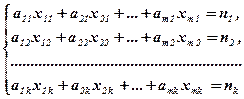 (14)
(14) (
(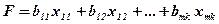 (16)
(16)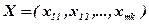 удовлетворяющее системам (13) и (14) и условию (15), при котором функция (16) принимает минимальное значение.
удовлетворяющее системам (13) и (14) и условию (15), при котором функция (16) принимает минимальное значение. (условие комплектности). Каждая единица материала может быть раскроена п различными способами, причем использование i - го способа (
(условие комплектности). Каждая единица материала может быть раскроена п различными способами, причем использование i - го способа ( ) дает
) дает  единиц k-го изделия (
единиц k-го изделия ( ).
).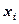 — число единиц материала, раскраиваемых i -м способом, и х — число изготавливаемых комплектов изделий.
— число единиц материала, раскраиваемых i -м способом, и х — число изготавливаемых комплектов изделий. (17)
(17) (18)
(18) (19)
(19) принимает максимальное значение.
принимает максимальное значение. ; х — число комплектов брусьев.
; х — число комплектов брусьев.


 ) может быть раскроена п различными способами, причем использование i-го способа (
) может быть раскроена п различными способами, причем использование i-го способа ( единиц k-го изделия (
единиц k-го изделия (  единиц.
единиц. , удовлетворяющее системе
, удовлетворяющее системе



