
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
О разновидностях моделированияСтр 1 из 4Следующая ⇒
Введение Настоящая глава посвящена той из компьютерных технологий обработки информации, ради которой когда-то создали первую ЭВМ и ради которой сегодня. В значительной мере создают супер-ЭВМ - решению прикладных научно-технических задач, среди которых задачи математического моделирования составляют видную долю. Абстрактное моделирование с помощью компьютеров - вербальное, информационное, математическое - в наши дни стало одной из информационных технологий, в познавательном плане исключительно мощной. Изучение компьютерного математического моделирования открывает широкие возможности для осознания связи информатики с математикой и другими науками - естественными и социальными. В данной главе, в значительной степени на примерах моделей из разных областей знания, показаны некоторые типичные задачи компьютерного математического моделирования. Их решение способствует выработке тех навыков, которые необходимы специалисту в области информатики. Отметим, что, говоря о математических моделях, мы имеем в виду сугубо прикладной аспект. В современной математике есть достаточно формализованный подход к понятию «математическая модель». Внутри него вполне допустимо игнорировать вопрос о связи математики с реалиями физического мира. В этом подходе моделями являются, например, система целых чисел, система действительных чисел, евклидова геометрия, алгебраическая группа, топологическое пространство и т.д. К исследованию таких формальных моделей вполне можно подключить компьютеры, но все равно это останется «чистой» математикой. В данной главе термин «математическая модель» увязывается с некоторой предметной областью, сущностью окружающего мира. Компьютерное математическое моделирование в разных своих проявлениях использует практически весь аппарат современной математики. В данной главе предполагается знание основ математики: * теории дифференциальных уравнений; * аппроксимации функций (включая интерполяцию и среднеквадратичные принижения); * аналитической геометрии на плоскости и в пространстве; * математической статистики; * численных методов: а) решения алгебраических и трансцендентных уравнений; б) решения систем линейных алгебраических уравнений;
в) интегрирования обыкновенных дифференциальных уравнений и их систем (задача Кош и). В тех немногих случаях, когда используемый математический аппарат выходит за пределы объема, традиционно считающегося достаточным для подготовки специалиста по информатике, минимально необходимые сведения приводятся в тексте. Понятие о компьютерном математическом моделировании Примеры задач линейного программирования 1. Задача об испо л ьзовании ресурсов (задача планирования производства) 1.1. Для изготовления двух видов продукции Таблица 1.
Прибыль, получаемая от единицы продукции Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Решение. Составим экономико-математическую модель задачи. Обозначим
По смыслу задачи переменные
Суммарная прибыль
Итак, экономико-математическая модель задачи: найти такой план выпуска продукции Задачу легко обобщить на случай выпуска п видов продукции с использованием т видов ресурсов. Обозначим
Тогда экономико-математическая модель задачи об использовании ресурсов в общей постановке примет вид: найти такой план
и условию
при котором функция
принимает максимальное значение. Задача о раскрое материалов На раскрой (распил, обработку) поступает материал одного образца в количестве, а единиц. Требуется изготовить из него l разных комплектующих изделий в количествах, пропорциональных числам Необходимо найти план раскроя, обеспечивающий максимальное число комплектов. Составим экономико-математическую модель задачи. Обозначим Так как общее количество материала равно сумме его единиц, раскраиваемых различными способами, то
Требование комплектности выразится уравнениями
Очевидно, что
Экономико-математическая модель задачи: найти такое решение Для изготовления брусьев длиной 1,2 м, 3 м и 5 м в соотношении 2:1:3 на распил поступают 195 бревен длиной 6 м. Определить план распила, обеспечивающий максимальное число комплектов. Составить экономико-математическую модель задачи. Решение. Прежде всего, определим всевозможные способы распила бревен, указав соответствующее число получаемых при этом брусьев (табл. 3). Таблица 3
Обозначим: Учитывая, что все бревна должны быть распилены, а число брусьев каждого размера должно удовлетворять условию комплектности, экономико-математическая модель задачи примет вид:
при ограничениях:
Задачу о раскрое легко обобщить на случай т раскраиваемых материалов. Пусть каждая единица j-го материала ( Обозначим Экономико-математическая модель задачи о раскрое в общей постановке примет вид: найти такое решение
и условию Задача о потребностях сырья Для производства двух видов изделий А и В предприятие (участок работы) использует три вида сырья. Нормы расхода сырья каждого вида на изготовление единицы продукции данного вида приведены в табл. 4. В ней же указаны прибыль от реализации одного изделия каждого вида и общее количество сырья данного вида, которое необходимо предприятию. Принимаем, что сбыт обеспечен и что изделия А и В могут производиться в любых соотношениях. Перед менеджером по выпуску товара поставлена задача составить такой план выпуска, при котором прибыль предприятия (участка работы) от реализации всех изделий была бы максимальной.
Таблица 4
Решение. Предположим, что предприятие изготовит
Общая прибыль от реализации Таким образом, мы приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение. Найдем решение сформулированной задачи, используя ее геометрическую интерпретацию. Сначала определим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств и найдем соответствующие прямые:
Эти прямые изображены на рис. 4.1. Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой — нет. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли ее координаты данному неравенству. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка, в противном случае — другая полуплоскость. Найдем, например, полуплоскость, определяемую неравенством
Для этого, построив прямую
Значит, полуплоскость, которой принадлежит точка O(0,0), определяется неравенством
Это и показано стрелками на рис. 6.1. Пересечение полученных полуплоскостей и определяет многоугольник решений данной задачи. Как видно из рис. 6.1, многоугольником решений является пятиугольник OABCD. Координаты любой точки, принадлежащей этому пятиугольнику, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую пятиугольнику OABCD, в которой функция F принимает максимальное значение.
Чтобы найти указанную точку, построим вектор С = (30, 40) н прямую
Если теперь взять какую-нибудь точку, принадлежащую построенной прямой и многоугольнику решений, то ее координаты определяют такой план производства изделий А и В, при котором прибыль от их реализации равна 480 руб. Далее, полагая h равным некоторому числу больше 480, мы будем получать различные параллельные прямые. Если они имеют общие точки с многоугольником решений, то эти точки определяют планы производства изделий А и В, при которых прибыль от их реализации превзойдет 480 руб. Перемещая построенную прямую
в направлении вектора С, видим, что последней общей точкой ее с многоугольником решений задачи служит точка В. Координаты этой точки и определяют план выпуска изделий А и В, при котором прибыль от их реализации будет максимальной. Найдем координаты точки В как точки пересечения прямых
Решив эту систему уравнений, получим
Варианты заданий
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 11
Вариант 12
Вариант 13
Вариант 14
Вариант 15
Вариант 16
Вариант 17
Вариант 18
Вариант 19
Вариант 20
Вариант 21
Вариант 22
Вариант 23
Вариант 24
[1] В ряде работ по математическому программированию стандартную задачу называют симметричной, а каноническую – основной. Введение Настоящая глава посвящена той из компьютерных технологий обработки информации, ради которой когда-то создали первую ЭВМ и ради которой сегодня. В значительной мере создают супер-ЭВМ - решению прикладных научно-технических задач, среди которых задачи математического моделирования составляют видную долю. Абстрактное моделирование с помощью компьютеров - вербальное, информационное, математическое - в наши дни стало одной из информационных технологий, в познавательном плане исключительно мощной. Изучение компьютерного математического моделирования открывает широкие возможности для осознания связи информатики с математикой и другими науками - естественными и социальными. В данной главе, в значительной степени на примерах моделей из разных областей знания, показаны некоторые типичные задачи компьютерного математического моделирования. Их решение способствует выработке тех навыков, которые необходимы специалисту в области информатики. Отметим, что, говоря о математических моделях, мы имеем в виду сугубо прикладной аспект. В современной математике есть достаточно формализованный подход к понятию «математическая модель». Внутри него вполне допустимо игнорировать вопрос о связи математики с реалиями физического мира. В этом подходе моделями являются, например, система целых чисел, система действительных чисел, евклидова геометрия, алгебраическая группа, топологическое пространство и т.д. К исследованию таких формальных моделей вполне можно подключить компьютеры, но все равно это останется «чистой» математикой. В данной главе термин «математическая модель» увязывается с некоторой предметной областью, сущностью окружающего мира. Компьютерное математическое моделирование в разных своих проявлениях использует практически весь аппарат современной математики. В данной главе предполагается знание основ математики: * теории дифференциальных уравнений; * аппроксимации функций (включая интерполяцию и среднеквадратичные принижения); * аналитической геометрии на плоскости и в пространстве; * математической статистики; * численных методов: а) решения алгебраических и трансцендентных уравнений; б) решения систем линейных алгебраических уравнений; в) интегрирования обыкновенных дифференциальных уравнений и их систем (задача Кош и). В тех немногих случаях, когда используемый математический аппарат выходит за пределы объема, традиционно считающегося достаточным для подготовки специалиста по информатике, минимально необходимые сведения приводятся в тексте. О разновидностях моделирования С понятием «модель» мы сталкиваемся с детства. Игрушечный автомобиль, самолет или кораблик для многих были любимыми игрушками, равно как и плюшевый медвежонок или кукла. В развитии ребенка, в процессе познания им окружающего мира, такие игрушки, являющиеся, по существу, моделями реальных объектов, играют важную роль. В подростковом возрасте для многих увлечение авиамоделированием, судомоделированием, собственноручным созданием игрушек похож на реальные объекты, оказало влияние на выбор жизненного пути. Что же такое модель? Что общего между игрушечным корабликом и рисунком на экране компьютера, изображающим сложную математическую абстракцию? И все же общее есть: и в том, и в другом случае мы имеем образ реального объекта или явления, «заместителя» некоторого «оригинала», воспроизводящего его с той или иной достоверностью и подробностью. Или то же самое другими словами: модель является представлением объекта в некоторой форме, отличной от формы его реального существования. Практически во всех науках о природе, живой и неживой, об обществе, построение и использование моделей является мощным орудием познания. Реальные объекты и процессы бывают столь многогранны и сложны, что лучшим способом их изучения часто является построение модели, отображающей лишь какую-то грань реальности и потому многократно более простой, чем эта реальность, и исследование вначале этой модели. Многовековой опыт развития науки доказал на практике плодотворность такого подхода. В моделировании есть два заметно разных пути. Модель может быть похожей копией объекта, выполненной из другого материала, в другом масштабе, с отсутствием ряда деталей. Например, это игрушечный кораблик, самолетик, домик из кубиков и множество других натурных моделей. Модель может, однако, отображать реальность более абстрактно - словесным описанием в свободной форме, описанием, формализованным по каким-то правилам, математическими соотношениями и т.д. В прикладных областях различают следующие виды абстрактных моделей: · традиционное (прежде всего для теоретической физики, а также механики, химии, биологии, ряда других наук) математическое моделирование без какой-либо привязки к техническим средствам информатики; · информационные модели и моделирование, имеющие приложения в информационных системах; · вербальные (т.е. словесные, текстовые) языковые модели; · информационные (компьютерные) технологии, которые надо делить А) на инструментальное использование базовых универсальных программных средств (текстовых редакторов, СУБД, табличных процессоров, телекоммуникационных пакетов); Б) на компьютерное моделирование, представляющее собой • вычислительное (имитационное) моделирование; • «визуализацию явлений и процессов» (графическое моделирование), • «высокие» технологии, понимаемые как специализированные прикладные технологии, использующие компьютер (как правило, в режиме реального времени) в сочетании с измерительной аппаратурой, датчиками, сенсорами и т.д. Итак, укрупненная классификация абстрактных (идеальных) моделей такова. 1. Вербальные (текстовые) модели. Эти модели используют последовательности предложений на формализованных диалектах естественного языка для описания той или иной области действительности (примерами такого рода моделей являются милицейский протокол, правила дорожного движения). 2. Математические модели - очень широкий класс знаковых моделей скованных на формальных языках над конечными алфавитами), широко использующих те или иные математические методы. Например, можно рассмотреть математическую модель звезды. Эта модель будет представлять собой сложную систему уравнений, описывающих физические процессы, происходящие в недрах звезды. Математической моделью другого рода являются, например, математические соотношения, позволяющие рассчитать оптимальный (наилучший с экономической точки зрения) план работы какого-либо предприятия. 3. Информационные модели - класс знаковых моделей, описывающих информационные процессы (возникновение, передачу, преобразование и использование информации) в системах самой разнообразной природы. Граница между вербальными, математическими и информационными моделями может быть проведена весьма условно; вполне возможно считать информационные модели подклассом математических моделей. Однако, в рамках информатики как самостоятельной науки, отделенной от математики, физики, лингвистики и других наук, выделение информационных моделей в отдельный класс является целесообразным. Отметим, что существуют и иные подходы к классификации абстрактных моделей; общепринятая точка зрения здесь еще не установилась. В частности, есть тенденция резкого расширения содержания понятия «информационная модель», при котором информационное моделирование включает в себя и вербальные, и математические модели. Основное содержание данной главы связано с прикладными математическими моделями, в реализации которых используются компьютеры. Это вызвано тем, что внутри информатики именно компьютерное математическое и компьютерное информационное моделирование могут рассматриваться как ее составные части. Компьютерное математическое моделирование связано с информатикой технологически; использование компьютеров и соответствующих технологий обработки информации стало неотъемлемой и необходимой стороной работы физика, инженера, экономиста, эколога, проектировщика ЭВМ и т.д. Неформализованные вербальные модели не имеют столь явно выраженной привязки к информатике - ни в принципиальном, ни в технологическом аспектах.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.45.92 (0.136 с.) |
 и
и  используют четыре вида ресурсов
используют четыре вида ресурсов 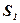 ,
,  ,
,  и
и  . Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в табл. 1 (цифры условные).
. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в табл. 1 (цифры условные). и
и  — число единиц продукции соответственно
— число единиц продукции соответственно  ) единиц ресурса
) единиц ресурса 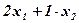 ) единиц ресурса
) единиц ресурса  ) единиц ресурса
) единиц ресурса  ; единиц ресурса
; единиц ресурса  (1)
(1) ,
,  . (2)
. (2) составит
составит  руб. от реализации продукции
руб. от реализации продукции  руб. — от реализации продукции
руб. — от реализации продукции 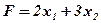 (3)
(3) , удовлетворяющий системе (1) и условию (2), при котором функция (3) принимает максимальное значение.
, удовлетворяющий системе (1) и условию (2), при котором функция (3) принимает максимальное значение. (j = 1, 2,..., п) — число единиц продукции
(j = 1, 2,..., п) — число единиц продукции  , запланированной к производству;
, запланированной к производству;  (i =1, 2,..., т) — запас ресурса
(i =1, 2,..., т) — запас ресурса  ,
,  – число единиц ресурса
– число единиц ресурса  — прибыль от реализации единицы продукции
— прибыль от реализации единицы продукции  выпуска продукции, удовлетворяющий системе
выпуска продукции, удовлетворяющий системе (4)
(4) , (5)
, (5) (6)
(6) (условие комплектности). Каждая единица материала может быть раскроена п различными способами, причем использование i - го способа (
(условие комплектности). Каждая единица материала может быть раскроена п различными способами, причем использование i - го способа ( ) дает
) дает  единиц k-го изделия (
единиц k-го изделия ( ).
).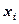 — число единиц материала, раскраиваемых i -м способом, и х — число изготавливаемых комплектов изделий.
— число единиц материала, раскраиваемых i -м способом, и х — число изготавливаемых комплектов изделий. (17)
(17) (18)
(18) (19)
(19) принимает максимальное значение.
принимает максимальное значение. ; х — число комплектов брусьев.
; х — число комплектов брусьев.


 ) может быть раскроена п различными способами, причем использование i-го способа (
) может быть раскроена п различными способами, причем использование i-го способа ( единиц k-го изделия (
единиц k-го изделия (  единиц.
единиц. — число единиц j-го материала, раскрываемого i-м способом.
— число единиц j-го материала, раскрываемого i-м способом. , удовлетворяющее системе
, удовлетворяющее системе
 , при котором функция
, при котором функция 
 .
. . Это и будет целевая функция.
. Это и будет целевая функция. ;
; 

 , возьмем какую-нибудь точку, принадлежащую одной из двух полученных полуплоскостей, например, точку O(0,0). Координаты этой точки удовлетворяют неравенству
, возьмем какую-нибудь точку, принадлежащую одной из двух полученных полуплоскостей, например, точку O(0,0). Координаты этой точки удовлетворяют неравенству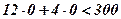

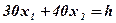 , где h — некоторая постоянная, такая, что прямая
, где h — некоторая постоянная, такая, что прямая  (см. рис.1).
(см. рис.1).
 .
. ,
,  . Следовательно, если предприятие изготовит 12 изделий вида А и 18 изделий вида В, то оно получит максимальную прибыль, равную
. Следовательно, если предприятие изготовит 12 изделий вида А и 18 изделий вида В, то оно получит максимальную прибыль, равную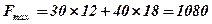 .
.


