
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление абсолютной и относительной
Погрешностей измерений при прямых измерениях Абсолютная погрешность Оценить отклонение каждого из результатов измерения от истинной величины можно лишь при наличии данных большого числа измерений с использованием теории вероятности. Однако на практике, в лабораторных условиях проводят 3-5 измерений. В этом случае абсолютная погрешность отдельного i-го измерения будет следующей: |DАi| = |АСР - Аi|, где АСР - средняя величина размера А. Средняя арифметическая величина всех ЅDАiЅ значений
называется абсолютной погрешностью опыта. Окончательный результат измерения может быть записан в виде А = АСР ± DАСР, где А - искомая величина, которая лежит внутри интервала АСР ± DАСР. l = (75.5 ± 0.3) см. Это означает, что истинное значение длины заготовки лежит в интервале от 75.2 см до 75.8 см. При этом не имеет смысла вычислять среднее значение с большим числом знаков после запятой, так как от этого точность не увеличивается. Относительная погрешность Абсолютная погрешность измерения не характеризует точности проведенных измерений. Поэтому для того, чтобы сравнить точность различных измерений и величин разной размерности, находят среднюю относительную погрешность результата (ЕА). Относительная погрешность определяется отношением абсолютной погрешности к среднему арифметическому значению измеряемой величины, которая определяется в процентах: ЕА= Относительная погрешность показывает, какая часть абсолютной погрешности приходится на каждую единицу измеренной величины. Это дает возможность оценить точность проведенных измерений, качество работы. Так, например, пусть при измерении бруска длиной l = 1.51 см была допущена абсолютная погрешность 0.03 мм, а при измерении расстояния от Земли до Луны L = 3.64 . 105 км абсолютная погрешность составила 100 км. Может показаться, что первое измерение выполнено намного точнее второго. Однако о точности измерения можно судить по относительной погрешности, а она показывает, что второе измерение было выполнено в семь раз точнее первого:  100% = 0.2% 100% = 0.2%
и ЕL = Вычисление абсолютных и относительных погрешностей при косвенных [2] измерениях В большинстве случаев при выполнении физических экспериментов исследуемая величина не может быть измерена непосредственно, а является функцией одной или нескольких переменных, измеренных непосредственно. При косвенных измерениях абсолютная и относительная погрешности результатов измерений находятся вычислением через абсолютные и относительные погрешности непосредственно измеренных величин.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.122.140 (0.009 с.) |

 100%.
100%.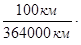 100% = 0.03%.
100% = 0.03%.


