
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет устойчивости стенки на глубинный сдвигСодержание книги
Поиск на нашем сайте
Расчет выполняется для эксплуатационного случая. Устойчивость стенки на глубинный сдвиг обеспечивается, если выполняется условие:
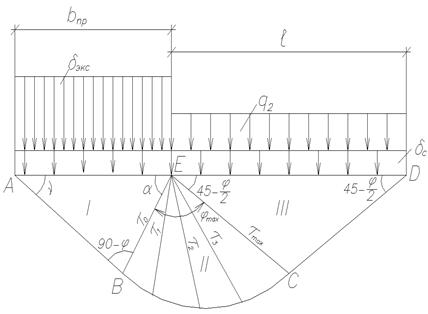
где F – суммарное значение сдвигающих нагрузок (в расчете принимается F = E а); γ c – коэффициент условия работ (для крупных, средних и мелких песков γ c=1,0, для песков пылеватых и глинистых грунтов γ c=0,9 в основании); γ n – коэффициент надежности по назначению сооружения, принимается соответственно равным 1,2; 1,15; 1,1 соответственно для сооружений I, II, III классов. Для определения силы предельного сопротивления R с на участке сдвига с выпором следует применять метод теории предельного равновесия. При этом профиль поверхности скольжения, ограничивающей область предельного состояния, принимается в виде двух отрезков прямых AB и DC, соединенных между собой кривой вставкой, описываемой уравнением логарифмической спирали (рис. 9). Все углы, используемые в расчетах задают в градусах, за исключением специально отмеченных случаев. Для построения кривой несущей способности основания задаются углами наклона равнодействующей, принимая их в долях от угла внутреннего трения:
где i = 1; 2; 3; 4. Внецентренное приложение нагрузки характеризуется появлением неравномерных напряжений в основании под подошвой стенки, поэтому действительный внецентренно загруженный фундамент заменяется эквивалентным, центрально нагруженным с приведенной шириной подошвы b пр, определяемой по формуле (эксцентриситет подставляется со своим знаком):
При определении R с сцепление грунта основания по своему действию принимается тождественным приложению внешней равномерно распределенной нагрузки в виде нормального напряжения
Связь между углом наклона равнодействующей к вертикали и ориентировкой треугольника предельного равновесия, определяется углом ν, который находится по формуле:
Далее определяются характеристики призмы обрушения ABCD. Линия АВ проводится под углом ν, линия ЕВ – под углом α к основанию
Линия ЕС строится под углом (450 – φ /2) к горизонтальной поверхности основания. Профиль, ограничивающий поверхности скольжения промежуточной зоны II, строится по уравнению логарифмической спирали. Радиус её кривизны определяется по формуле:
где r 0 – начальный радиус, r 0 = ЕВ и определяется по теореме синусов,
y max – показатель степени, подставляется в радианах,
Линия CD проводится через точку D под углом (45о – φ /2) к горизонтальной поверхности ED. Положение точки D на длине составляющей призмы обрушения определяется по формуле:
После определения очертания призмы обрушения находятся веса Р 1, Р 2, Р 3 её отдельных зон (I, II, III):
где F i – площадь одной из зон, определяется по формулам:
Сила сопротивления сдвига вычисляется по формуле:
где
здесь
По найденному значению R u определяются значения σ и τ, по которым строится кривая несущей способности основания:
Эксплуатационное напряжение находится по формуле:
Для построения криволинейной части участка II призмы обрушения делим его на четыре части и определяем значение угловых координат
Определение суммарной силы сопротивления по формуле:
где τэкс – суммарное касательное напряжение сил сопротивления (принимается по результатам расчета на ЭВМ по программе Grunt.exe). Если условие (9.1) устойчивости на глубинный сдвиг не выполняется, необходимо заменить грунт основания на грунт засыпки, на глубину 2 b.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.52.54 (0.006 с.) |

 ,
,
 ,
,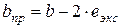 .
.
 .
.
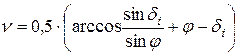 .
.
 .
.
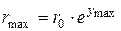 ,
,
 ;
; ;
;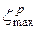 – угловая координата радиуса, рад.,
– угловая координата радиуса, рад.,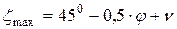 ;
;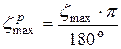 .
.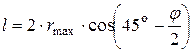 .
. ,
,
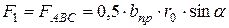 ;
; ;
;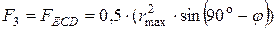 .
.
 ,
,
 < 0;
< 0;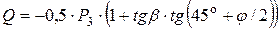 ;
;
 > 90о.
> 90о.
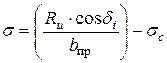 ;
;  .
.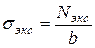 .
.
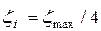 и радиусов
и радиусов 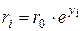 . Здесь yi – показатель степени основания натурального логарифма для i -го участка, определяется по формуле:
. Здесь yi – показатель степени основания натурального логарифма для i -го участка, определяется по формуле:
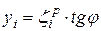 .
.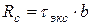 ,
,



