Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Швидкі алгоритми дискретних косинус і синус-перетворень Фур’є
Дискретне косинус-перетворення Фур’є (ДКПФ) і дискретне синус-перетворення Фур’є (ДСПФ), а також відповідні швидкі алгоритми (ШКПФ і ШСПФ) забезпечують безнадлишкове виконання дискретного перетворення Фур’є (ДПФ) і Хартлі (ДПХ) комплексної, дійсної, комплексно-спряженої, парної або непарної послідовності [4]. При цьому розпаралелюється обробка дійсної, комплексно-спряженої і комплексної послідовностей. Нехай x(n), n=0,1,…,N-1,N=2m , m=1,2,3…- дійсна послідовність, xc(n) і xs(n) – відповідно її парна (4.19) і непарна (4.20) частини
xc(n)=xc(N-n)={x(n)+x(N-n)}/2, n=0,1,…,N/2; (4.19) xs(n)=-xs(N-n)={x(n)-x(N-n)}/2, n=0,1,…,N/2; (4.20) так, що x(n)=xc(n)+xs(n), n=0,1,…,N-1, і нехай HC(k)=ДКПФN{xc(n)}, HS(k)=ДСПФN{xs(n)}, HC(k)= де CrN=cos(2пr/N), S'rN= sin(2пr/N), xc(n)=ДКПФ-1N{HC(k)} = N ДКПФ{HC(k)},xs(n) = ДСПФ-1N{HS (k)} = ДСПФ{HS(k)}.
Серед відомих [4] алгоритмів ШКПФ і ШСПФ простотою реалізації відрізняються алгоритми, побудовані за методом Рейдера-Бреннера (ШКПФРБ і ШСПФРБ). Їх графи загалом зберігають схему зв’язків алгоритмів за основою два, але за кількістю множень відповідають алгоритмам за розщепленою основою і мають дуже просту базову операцію “дійсний метелик”. Тому віддамо їм перевагу при реалізації ШКПФ і ШСПФ на потокових обчислювальних структурах. Формули розкладу (ФР) алгоритмів ШКПФ і ШСПФ відповідно задаються виразами
HC(2k) = ДКПФN/2 {xc(n) + xc(N/2+ n)}; HC(I) = A(0), HC(2k+1) = 2A(k) -HC(2k-1), k=1,2,...N/2-2; (4.21) HS(2k) = ДСПФN/2{xs(n)+xs(N/2+n)}; HS(I) = B(0), HS(2k+1) = 2B(k) +HS(2k-1), k=1,2,....N/2-2, (4.22) де A(k)=ДКПФN/2{[xc(n)-xc(N/2+n)]CnN}, B(k)=ДCПФN/2{[xs(n)-xs(N/2+n)]SnN}.
На їх основі N-точкове ДКПФ розбивається на два N/2-точкові ДКПФ, а N-точкове ДСПФ - на ДСПФN/2 і ДКПФN/2. Рекурсивно застосовуючи ФР (4.21) і (4.22) до перетворень меншої розмірності, отримуємо алгоритми ШКПФРБ і ШСПФРБ [4]. Ці алгоритми мають близькі схеми реалізації обчислень, які достатньо просто реалізуються на одному і тому ж пристрої. Так, на рис. 4.9 наведений узагальнений граф алгоритмів ШКПФРБ і ШСПФРБ для N=16.
Рис 4.9. Узагальнений граф алгоритму ШКПФРБ і ШСПФРБ для N=16 Для першого з них використовуються множники r=s=1, Rn=C16 n Порівняльний аналіз приведеного та відомого графа алгоритму комплексного ШПФ Кулі-Тьюкі за основою два (ШПФк2) з частотним прорідженням [4], показує співпадіння їх структури на m=log2N основних етапах переходу до перетворень меншої розмірності. При цьому використовується суттєво спрощена базова операція, що виконується над дійсними даними при дійсних фазових множниках (рис.4.10).
Рис.4.10 Базові операції алгоритмів ШКПФ-ШСПФ
На двох останніх етапах фазові множники приймають тривіальне значення, і тому на графі не показані. Крім того, в алгоритмах ШКПФРБ-ШСПФРБ додатково введений етап виділення парної за (4.19) чи непарної за (4.20) складових вхідної послідовності, а також m=log2N-1 етапів додавань, на яких здійснюється перехід від проміжних перетворень A(k) чи B(k) до необхідних HC(k) і HS(k).
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.196.223 (0.006 с.) |
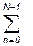 xc(n) CknN, HS(k)=
xc(n) CknN, HS(k)= 
 , на виході маємо P(k)=HC(k), а для другого r=0, S=-1, Rn=S16n, P(k)=HS(k).
, на виході маємо P(k)=HC(k), а для другого r=0, S=-1, Rn=S16n, P(k)=HS(k).