
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамическое программирование. Классические задачи динамического программирования. Функциональное уравнение Беллмана.Содержание книги
Поиск на нашем сайте
Ответы МО практика 1. Сформулировать алгоритм и произвести расчет двух итераций нахождения точки экстремума функции f(x) = 2x (3 - x) + 4 ® max; L0 = [-2, 6]; l0 = 0.7; l0 > e ³ l0/2 методами дихотомии и золотого сечения.
2. Сформулировать алгоритм и произвести расчет двух итераций нахождения точки экстремума функции f(x) = 2 + x (5 + 3x) ® min; L0 = [-2, 3]; l0 = 0.4; l0 > e ³ l0/2 методами дихотомии и Фибоначчи.
3. Сформулировать алгоритм и произвести расчет двух итераций нахождения точки экстремума функции f(х)=x2+2х ® min; L0 = [-3, 5]; e ≤ 0,2 методами дихотомии и золотого сечения.
4. Сформулировать алгоритм и произвести расчет двух итераций нахождения точки экстремума функции f(х)=x2+2х ® min; L0 = [-3, 5]; e ≤ 0,2 методами дихотомии и Фибоначчи.
10. Сформулировать алгоритм и произвести расчет двух итераций для нахождения экстремума (| min |) целевой функции f (x) = x 12 – 4 x 1 + 2 х 22 + 2 х 2, используя метод пропорционального градиентного поиска, начиная с точки Х0 = (1, 0).
11. Сформулировать алгоритм и произвести расчет двух итераций для нахождения экстремума (| min |) целевой функции f (x) = x 12 – 4 x 1 + 2 х 22 + 2 х 2, используя метод наискорейшего подъема (спуска), начиная с точки Х0 = (1, 0).
15. Построить двойственную задачу и осуществить расчет двух шагов решения: 4 x 1 + x 2 + x 3 + 2 x 4 + x 5 ® max 4 x 1 + x 2 - x 3 - x 4 + x 5 ³ 9 x 1 + x 2 - x 3 + x 4 - 6 x 5 = 10 - x 1 - x 3 + 5 x 5 £ 1 x 1, x 2, x 3, x 4, x 5 ³ 0
Так как исходная задача на максимизацию, то приведем все неравенства системы ограничений к виду £ для чего обе части первого неравенства умножим на (-1) Получим:
-4 x 1 - x 2 + x 3 + x 4 - x 5 £ -9 x 1 + x 2 - x 3 + x 4 - 6 x 5 = 10 - x 1 - x 3 + 5 x 5 £ 1 Составим расширенную матрицу системы
Транспонируем матрицу
Сформулируем двойственную задачу:
Z=9y1+10y2+y3 min
4y1+y2-y3 ³ 4 y1+y2 ³ 1 -y1-y2-y3 ³ 1 -y1+y2 ³ 2 y1-6y2+5y3 ³ 1 y1<=0 y2><0 y3>=0
4y1+y2-y3+y4 = 4 y1+y2 +y5 = 1 -y1-y2-y3 +y6 = 1 -y1+y2 +y7= 2 y1-6y2+5y3 +y8= 1
y4=4; y5=1; y6=1; y7=2; y8=1 первое допустимое решение
Составим симплекс таблицу
. -4 минимальный свободный элемент -9/-4 Y4 в свободные, y1 в базис
Составим симплекс таблицу
Y7 мин своб элемент
Y7 в свободные Y2 в базис
16. Сформулировать алгоритм и осуществить расчет (не более 2-х итераций) решения транспортной задачи методом потенциалов. Исходный опорный план - методом северо-западного угла. Вектор поставок - (10, 3, 7); Вектор потребления - (1, 8, 7, 4); Матрица стоимости:
Методом северо-западного угла найти начальный план перевозок в транспортной задаче, заданной матрицей перевозок (табл. 4.2).Таблица 4.2
Решение: Начинаем вычисления по формуле (4.6) с северо-западного угла, т. е. с удовлетворения потребностей первого потребителя В1 за счет запасов первого поставщика А1: х11 =min[10,1]=1. Потребности в пункте В1 удовлетворены и, следовательно, х21 = х31 =0 (ставим точки, табл. 4.3). Первый столбец выбывает из рассмотрения. Остаток груза в пункте А1 составит (10–1)=9.Таблица 4.3
41. Проанализируем относительные оценки. Среди оценок имеется одна отрицательная: ∆32=–7. Поэтому данный план не является оптимальным. Его можно улучшить перераспределением поставок.
22. Находим потенциалы, составляя для каждой базисной клетки уравнение αi + βj = cij. Полагаем α1 =0. Тогда для базисных клеток (1,1), (1,2) и (1,3) имеем: α1 + β1 =1, α1 + β2 =7, α1 + β3 =3, откуда β 1 =1, β 2 =7, β 3 =3.Далее для базисных клеток (1,3), (2,1) и (3,2) имеем: α2 + β3 =2, α2 =2 – β3 =2 – 3= -1; α3 + β2 =6, α3 =6 – β2 =6–7= -1; α3 + β4 =10, β4 =10 – α3 =10+1= 11. 32. Для свободных клеток вычисляем относительные оценки:∆14==8–(11)=-3, ∆21==3–(1-1)=3, ∆22==4–(7-1)=-2, ∆24==2–(11-1)=-8,∆31==5–(1-1)=5, ∆33=9–(3-1)= 7. 42. Условие окончания ∆ij>0 не выполнено: ∆24= –8. 52. Для клетки (2,2) построим означенный цикл (табл. 4.16).
f =1∙1+7∙1+3∙4+8∙4+3∙2+7∙6=100.
17. Сформулировать алгоритм и осуществить расчет (не более 2-х итераций) решения транспортной задачи методом потенциалов. Исходный опорный план - методом Фогеля. Вектор поставок - (10, 10, 20); Вектор потребления - (10, 8, 2, 20); Матрица стоимостей:
Штраф — это разность между двумя наименьшими стоимостями в текущей строке(столбце). Находим в таблице значение максимального штрафа. Это значение 5. Далее находим столбцы и строки, в которых штраф принимает найденное значение. После этого в полученном множестве строк и столбцов находим элемент с наименьшей стоимостью.
Сравним значения а1 и b2 Т.к. b2<=a1, то получим X1,2=b2=8 A1=a1-X1,2=10-8=2 Вычеркиваем столбец 2 (потребителя B2 исключаем из рассмотрения) Найдем штрафы.
Сравним значения а1 и b4 Т.к. a1<=b4, то получим X1,2=a1=2
B4=b4-X1,4=20-2=18 a1=0 Вычеркиваем строку 1 (производителя a1 исключаем из рассмотрения) Найдем штрафы.
Сравним значения а2 и b3 Т.к. b3<=a2, то получим X1,2=b3=2
A2=a2-X2,3=10-2=8 b3=0 Вычеркиваем столбец 3 (потребителя b3 исключаем из рассмотрения) Найдем штрафы.
Сравним значения а2 и b1 Т.к. a2<=b1, то получим X1,2=a2=8
B1=b1-X2,1=10-8=2 a2=0 Вычеркиваем строку 2 (производителя a2 исключаем из рассмотрения) Найдем штрафы.
Поскольку в таблице осталась одна невычеркнутая строка, то перенесём значения из соответствующих Bj в оставшиеся незаполненные клетки таблицы, при этом значение a3 станет равным 0.
Все строки и столбцы таблицы вычеркнуты. Значит, получено допустимое базисное решение. Решение является базисным. Среди заполненных клеток нет нулевых элементов, это значит, что решение является невырожденным.
Суммарные затраты данного решения F=186.
Решение методом потенциалов.
21. Находим потенциалы, составляя для каждой базисной клетки уравнение αi + βj = cij. Полагаем β1 =0. Тогда для базисных клеток (2,1) и (3,1) имеем: Α2 + β1 =3, α3 + β1 =2, откуда α2 =2, α3 =4Далее для базисных клеток (1,3), (2,1) и (3,2) имеем: Α2 + β3 =2, β3 =2 – α2 =2–2= 0. Α3 + β4 =8, β4 =8 – α3 =8–4= 4. α1 + β4 =3, α1 =3 – β4 =3–4= -1; α1 + β2 =1, β2 =1 – α1 =1 +1= 2; 31. Для каждой свободной клетки вычисляем относительные оценки:∆ij= cij –(αi + βj)= cij – αi – βj ∆11==8–(0-1)=9, ∆13==3–(0-1)=4, ∆22==7–(2+2)=3, ∆24=6–(4+2)=0,∆32==6–(2-4)=8, ∆33=5–(0+4)= 4. 41. Проанализируем относительные оценки. Среди оценок нет отрицательных. Поэтому данный план является оптимальным. Минимальные затраты на транспортировку продукции:f =186.
18. Сформулировать алгоритм и произвести расчет двух итераций для нахождения экстремума (|max|) целевой функции f(x) = 3x13 – x1 – х23 – 3х22 – 1, используя метод пропорционального градиентного поиска, начиная с точки Х0 = (0, 0). Решение: Начальный этап. Зададим координаты начальной точки x (0) =(0;0). Выражение для градиента функции в произвольной точке gradf(x1,x2)= (9x12-1;-3x22-6x2)., начальный шаг h0 =1, дробление шага 0,5 Присваиваем k =0. Значение функции в начальной точке f( x(0) )=f (0;0)=-1. Присваиваем k =0. Основной этап: Шаг 10. gradf( x (0))= (-1;0). Шаг 20. Критерия останова нет. | gradf( x (k)) |=1, переходим к шагу 30. Шаг 30. Значение шага h0 =1. Шаг 40. Вычисляем координаты следующей точки: x (1)= x (0)–h0*gradf( x (0)) =(0;0)-1*(-1:0)=(1;0). Значение функции в точке x (1) f( x(1) ) = f (0,5;0)=1. Шаг 50. Проверяем выполнение условия f( x(1) )> f( x(0) ). Условие для k =0 выполнено (1>-1), поэтому не уменьшаем (дробим) шаг Шаг 11. В точке x (1) =(0,5;0) вычисляем градиент: gradf( x (1) = (-0,44;0) и его длину | gradf( x (1)) |≈0,44. Шаг 21. Критерия останова нет:. переходим к шагу 3. Шаг 31. Значение шага h1 = h0= 1. Шаг 41. Вычисляем координаты следующей точки: x (2)= x (1)–h1*gradf( x (1)) =(1; 0) –1*(-0,44;0))=(1,44;0). Значение функции f( x(2) ) = f (1,44;0)≈6,51. Шаг 51. Проверяем выполнение условия f( x(2) )< f( x(1) ). Условие для k =1 выполнено (6,51<1), Присваиваем k:=k+1 =2 и переходим к шагу 12. Готово. Данная задача не выполняется нормальным образом при дроблении шага. Например возьмем начальный шаг 0,5. Тогда значение функции будет не удовлетворять условию и придется дробить шаг. При 0,25 будет также и т.д. При шаге равном единице условие всегда будет удовлетворяться без дробления, но(!) при следующем шаге значение градиента будет 17,6. И при дроблении никогда не будет выполняться условие для продолжения действий. При шаге равном 0,5, но дроблению равном 2 также не будет выполняться условие, т.к. функция бесконечно растет.
19. Сформулировать алгоритм и произвести расчет двух итераций для нахождения экстремума (| max |) целевой функции f (x) = 3 x 13 – x 1 – х 23 – 3 х 22 – 1, используя метод наискорейшего подъема (спуска), начиная с точки Х0 = (0, 0).
Решение: Начальный этап. Зададим координаты начальной точки x (0) =(0;0). Выражение для градиента функции в произвольной точке gradf(x1,x2)= (9x12-1;-3x22-6x2) (см. пример 1). Присваиваем k =0. Основной этап: Шаг 10. В точке х( 0) значение функции f(x( 0))=-1, gradf( x (0))= (-1;0). Шаг 20. Критерия останова нет. | gradf( x (k)) |=1, переходим к шагу 30. Шаг 30. Определяем величину шага h0, для чего определим функцию φ(h0). 3 h0 3-h0-1. Найдем минимум функции φ(h0) по h0:
// это не понял Так как Шаг 40. Определяем координаты точки x (1): x (1)= x (0)–h0*gradf( x (0)) = (0;0) –0,33*(-1;0)=(0,33;0). Присваиваем k:=k+1= 1 и переходим к шагу 11. Шаг 11. В точке x (1)= (0,33;0) значение функции f(x( 1)) @-1,22, значение градиента gradf( x (1))= (0,49;0). Шаг 21. Критерия останова нет. | gradf( x (k)) |=0,49, переходим к шагу 30. Шаг 31. Определяем величину шага h1, для чего определим функцию φ (h1). = f( 0,33-0,49 h1;0) = =3(0,33-0,49h1)3-(0,33-0,49h1)-1. Найдем минимум функции φ(h1) по h1:
Шаг 41. Определяем координаты точки x (2): x (2)= x (1)–h1*gradf( x (1)) = (0,33;0)–1,35*(0,49;0)@(-0,33;0). Присваиваем k:=k+ 1 = 2 и переходим к шагу 12. Шаг 12. В точке x (2) = (-0,33;0) значение функции f(x( 2)) @-0,77,
20. Сформулировать алгоритм и решить задачу о назначениях венгерским методом (не более 2-х итераций). Матрица эффективности:
Исходная матрица имеет вид:
21. Сформулировать алгоритм и решить задачу о назначениях венгерским методом (не более 2-х итераций). Матрица эффективности:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.97.170 (0.013 с.) |






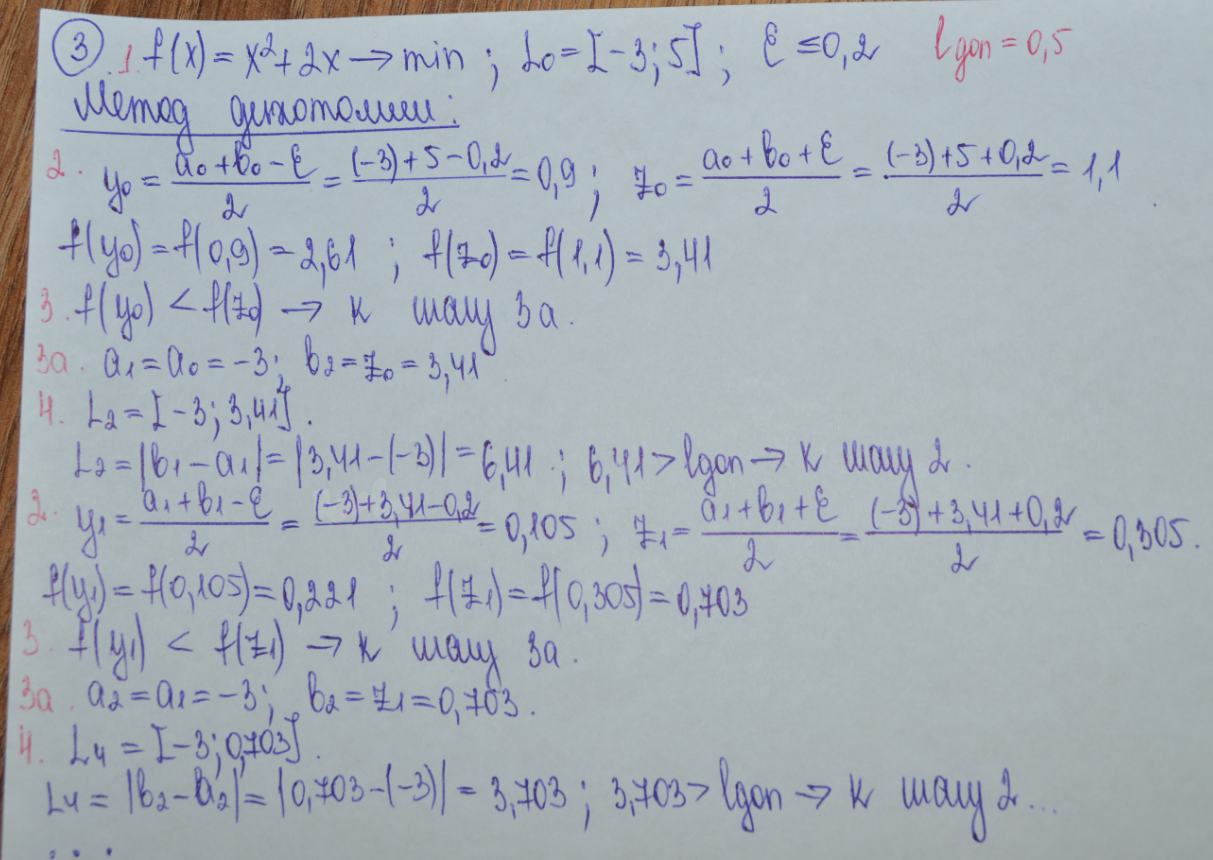



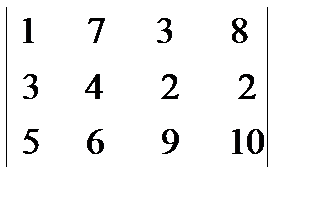
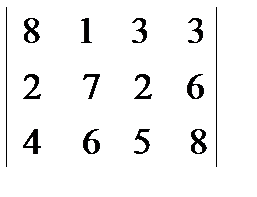
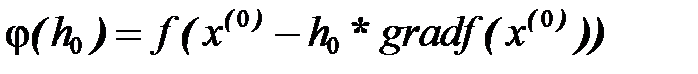 = f ((0;0) -h0* (-1;0))= f (h0;0) =
= f ((0;0) -h0* (-1;0))= f (h0;0) =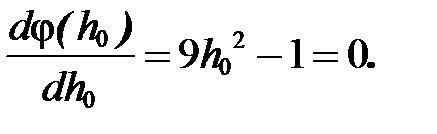 Отсюда h0@ 0,33.
Отсюда h0@ 0,33.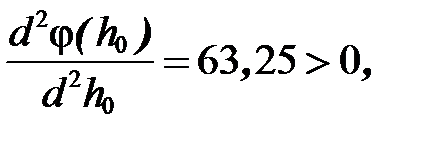 то найденное значение шага обеспечивает минимум функции φ(h0) по h0.
то найденное значение шага обеспечивает минимум функции φ(h0) по h0.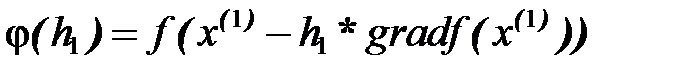 = f ((0,33;0)– h1* (0,49;0))=
= f ((0,33;0)– h1* (0,49;0))=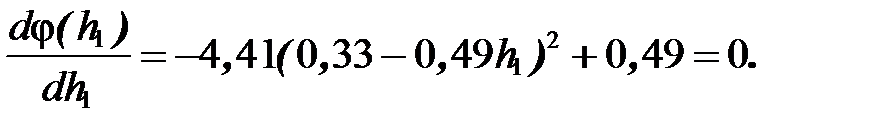 Отсюда h1@ 1,35.
Отсюда h1@ 1,35.



