
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Додаткові арифметичні команди FPU.Содержание книги
Поиск на нашем сайте
Додаткові команди належать до арифметичних, мають безоперандну форму. Всіх команд – 8. fsqrt – замінює вершину стека коренем квадратним з вмісту вершини стека. Якщо fscale – масштабування інтерпретує fscale; fprem – обчислює часткову остачу від ділення числа в fprem; st(0)= (st(0)) – q*(st(1)), де q – ціле число. Тут вміст регістра st(1) є модулем в операції обчислення остачі. Знак остачі збігається зі знаком початкового діленого. Опис команди: EXPDIF=exponent(st(0)) – exponent(st(1)); if EXPDIF<64 then q=ціле, яке одержується заокругленням (st(0)) st=(st) – (st(1))*q; c2=0; c0,c1,c3=три молодших біти q;(q2,q1,q0) else c2=1; n=число між 32 і 63; qq=ціле, яке одержується заокругленням (st(0)) st=(st) – ( fi; fprem працює методом ітераційного віднімання і може зменшити показник степеня в st не більше, ніж на 63 за одне своє виконання. Якщо в процесі виконання fprem одержується остача менша за модуль, то функція вважається виконаною і прапорець с2 встановлюється рівним 0. В противному випадку, прапорець с2 стає рівним 1, а результат в st називається неповною остачею. Програма може виконати команду ще раз і одержати повну (або нову неповну) остачу. Перевірку біта с2 можна за допомогою цілочислового пристрою: передача sw в ax, потім командою sahf переслати вміст регістра ah в регістр eflags і стан прапорця с2 показує прапорець pf. Інший спосіб: порівняння st(0) і st(1). Повна остача отримана, якщо (st(0)) менший (st(1)). fprem1 – як і команда fprem і обчислює остачу, яка одержується при діленні (st(0)) на (st(1)), причому величина повної остачі менша, ніж половина величини модуля. Опис команди: EXPDIF=exponent(st(0)) – exponent(st(1)); if EXPDIF<64 then q=ціле, яке одержується заокругленням (st(0)) st=(st) – (st(1))*q; c2=0; c0,c1,c3=три молодших біти q;(q2,q1,q0) else c2=1; n=число між 32 і 63; qq=ціле, яке одержується заокругленням (st(0)) st=(st) – ( fprem1 працює методом ітераційного віднімання і може зменшити показник степеня в st не більше, ніж на 63 за одне своє виконання. Якщо в процесі виконання fprem1 одержується остача менша за модуль, то функція вважається виконаною і прапорець с2 встановлюється рівним 0. В противному випадку, прапорець с2 стає рівним 1, а результат в st називається неповною остачею. Програма може виконати команду ще раз і одержати повну (або нову неповну) остачу. Перевірку біта с2 можна за допомогою цілочислового пристрою: передача sw в ax, потім командою sahf переслати вміст регістра ah в регістр eflags і стан прапорця с2 показує прапорець pf. Інший спосіб: порівняння st(0) і st(1). Повна остача отримана, якщо (st(0)) менший (st(1)). Команди fprem і fprem1 мають ще одну особливість, яку можна використати, застосовуючи команди обчислення тригонометричних функцій. Після повного завершення команди fprem і fprem1 (с2=0) біти с0, с3, с1 містять значення трьох молодших бітів частки, які логічно є числовими значеннями номера одного з восьми октантів одиничного круга. Це суттєво можна використати, працюючи з тригонометричними функціями. frndint – команда заокруглення до цілого. Заокруглює число в st до цілого. Режим заокруглення задається в полі rc регістра cw. fxtract – команда виділення компонентів числа з плаваючою крапкою. Компонентами такого числа є фактичний порядок і мантиса. Команда розщеплює (st) на порядок і мантису. Порядок перетворює в число з плаваючою крапкою в форматі РТ і записує його замість початкового числа. Мантиса як число в форматі РТ (знак збігається зі знаком початкового операнда, істинний порядок дорівнює 0, тобто зміщений порядок 16383=3fffh, мантиса дорівнює мантисі початкового операнда) записується в нову вершину стека. Якщо початковий операнд дорівнює нулеві, то команда fxtract утворює 0 в st(0), мінус безмежність в st(1) і фіксує особливий випадок “ділення на нуль”. Команду можна використовувати разом з командою fbstp для перетворення чисел з формату РТ в десятковий формат при виведенні на дисплей або принтер. Відзначимо, що командою fscale розщеплене число можна перетворити в початкове. Насамкінець ще дві команди: fabs – st(0)= fchs – st(0)= Команди порівняння FPU Використовуються для аналізу чисел на вершині стека (іноді відносно другого числа) і формування коду умови в sw. Команди дійсного порівняння: (st(0)) порівнюється з (src), а саме, з вмістом регістра, операндом в оперативній пам’яті (ОТ або ПТ). Якщо операнда немає, то порівнюються (st(0)) і (st(1)). В усіх командах порівняння знак нуля ігнорується, тобто fcom // src – порівнює (st(0)) зі вмістом src. Код умови відображує відношення між числами операндами. Операнди вважаються не порівнюваними або не упорядкованими, якщо хоча б один з них є не числом. zf pf cf
Після запису с3с2с1с0 в регістр fcomp // src – порівняння і вилучення зі стека. Операнд src – в ОП (ОТ або ПТ). Працює як і fcom, але додатково ще вилучає зі стека. fcompp – порівняння (st(0)) і (st(1)) та подвійного вилучення зі стека. Якщо будь-який з операндів є не числом або має не підтримуваний формат, або якщо виникає порушення стека, то формується особливий випадок “недійсна операція” і код умови показує не порівнювані (не упорядковані). ficom src – результат порівняння визначається в таблиці, наведеній вище. Операнд (src) – трактується як ціле число в форматі ЦС або КЦ, перетворюється у формат РТ і порівнюється з (st(0)). ficomp src – команда виконує такі ж дії як ficom і додатково ще вилучає зі стека. Операнд (src) – трактується як ціле число в форматі ЦС або КЦ, перетворюється у формат РТ і порівнюється з (st(0)). ОВ як і в інших командах порівняння. Три команди fucom/fucomp/fucompp – неупорядкованого дійсного порівняння. Вони порівнюють вершину стека з (src), який може бути тільки вмістом регістра st(i). Якщо без операнда, то st(1). Коди умови визначаються у вище наведеній таблиці. Якщо будь який операнд у цих командах порівняння є “тихе не число”, то команди не формують особливий випадок “недійсна операція”, хоча біти коду умови показують “неупорядковані”. Однак, якщо один з операндів є сигналізуючим не числом або поданий у не підтримуваному форматі, або виникає порушення стека, формується особливий випадок “недійсна операція”. fucomp – додатково вилучає зі стека вершину. fucompp – додатково вилучає зі стека вершину і підвершину. ftst – (без операнда) порівнює (st(0)) з нулем і формує код умови як вказано вище в таблиці. fxam – аналіз вмісту вершини стека, тобто (st(0)), і формування в коді умови с3с2с1с0 результату цього аналізу, а саме: с1= знаковий біт (st(0)) case (тип об’єкта в st(0)) of не підтримуваний формат: с3,с2,с0=0,0,0 не число: с3,с2,с0=0,0,1 нормалізоване число: с3,с2,с0=0,1,0 безмежність: с3,с2,с0=0,1,1 Нуль: с3,с2,с0=1,0,0 Порожній: с3,с2,с0=1,0,1 Денормалізоване число: с3,с2,с0=1,1,0
38. Команди трансцендентних функцій. Алгоритми обчислення значень функцій Команда Якщо операнд не припустимий, біт с2 коду умови установлюється в 1 і Команда Те, що
Зрозуміло, що в обох цих співвідношеннях Покажемо, що формули (38.1) і (38.2) справджуються. Для доведення формули (38.1) застосуємо до обох частин цієї формули функцію
Знайдемо
Оскільки
що Для доведення (38.2) застосуємо до обох частин функцію
Одержана рівність завершує доведення формули (38.2). Для обчислення за формулою (38.1) потрібно виконати наступні кроки. 1. Якщо 2. Записати 3. Обчислити значення виразу 4. Виконати команду Як результат цих дій в регістрі 1. Якщо 2. Обчислити значення виразу 3. Обчислити значення виразу 4. Виконати команду Як результат цих дій в регістрі Виконуючи команди Новими для 80387 і FPU є команди: обчислення синуса Команди Команда Якщо потрібно обчислити значення виразу
Вираз Якщо операнд в Отже, у виразі (38.3) легко обчислити показник степеня, тобто 1) спочатку запишемо 2) застосуємо команду 3) оскільки мантиса подана в нормалізованому вигляді, то вона за модулем більша або рівна 1. Тому для зведення мантиси до потрібного діапазону, якщо вона додатна, то від неї потрібно відняти 1 і до 4) Застосуємо команду 5) Виконаємо команду 6) Виконаємо команду 7) Застосуємо тепер команду Для обчислення логарифма за будь-якою основою можна використати формулу
Команда
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.4 (0.008 с.) |

 ,
, 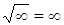 . 1) Виконується порівняно швидко як і команда ділення. 2) Точність команди відповідає точності звичайних арифметичних операцій (похибка результату відповідає половині молодшого біта мантиси). 3) В команді доступні режими заокруглення.
. 1) Виконується порівняно швидко як і команда ділення. 2) Точність команди відповідає точності звичайних арифметичних операцій (похибка результату відповідає половині молодшого біта мантиси). 3) В команді доступні режими заокруглення. , то виникає особлива ситуація “не дійсна операція”.
, то виникає особлива ситуація “не дійсна операція”. як ціле двійкове і додає його
як ціле двійкове і додає його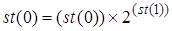 - це команда швидкого множення (
- це команда швидкого множення ( або ділення
або ділення 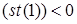 вмісту вершини стека на цілий степінь двійки.
вмісту вершини стека на цілий степінь двійки.  на
на 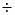 (st(1)) до нуля;
(st(1)) до нуля; до нуля;
до нуля; );
); ;
; .
. і
і  не розрізняються (рівні).
не розрізняються (рівні).
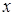



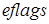 (
( і
і 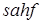 ) для переходу за результатом порівняння можна використовувати команди умовного переходу (
) для переходу за результатом порівняння можна використовувати команди умовного переходу (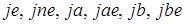 ). Для перевірки операндів не чисел використати команду
). Для перевірки операндів не чисел використати команду  . Команда fcom сигналізує про особливий випадок “недійсна операція”, якщо хоча б один з операндів є “тихим” не числом.
. Команда fcom сигналізує про особливий випадок “недійсна операція”, якщо хоча б один з операндів є “тихим” не числом. і
і 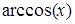 та логарифмів за будь-якою основою.
та логарифмів за будь-якою основою.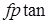 – обчислення часткового тангенса. Вона сприймає в
– обчислення часткового тангенса. Вона сприймає в 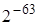 до
до  , яке вважається аргументом в радіанах. Повертає результат у двох верхніх регістрах стека: значення тангенса заданого кута
, яке вважається аргументом в радіанах. Повертає результат у двох верхніх регістрах стека: значення тангенса заданого кута  заміщує аргумент і в стек записується 1.0. Такі дії пояснюються сумісністю зі співпроцесорами 8087 і 80287, в яких команда
заміщує аргумент і в стек записується 1.0. Такі дії пояснюються сумісністю зі співпроцесорами 8087 і 80287, в яких команда 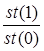 і значення в
і значення в  (
( ).
). залишається незмінним. Програмно потрібно операнд звести до значення, яке повинно знаходитися в діапазоні від
залишається незмінним. Програмно потрібно операнд звести до значення, яке повинно знаходитися в діапазоні від  . Щоб не виникло особливого випадку “недійсна операція”, регістр
. Щоб не виникло особливого випадку “недійсна операція”, регістр 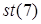 повинен бути порожнім.
повинен бути порожнім. – обчислення часткового арктангенса: обчислює
– обчислення часткового арктангенса: обчислює  . Після цього вилучення зі стека і кут заміщує два операнди у вершині стека. Результат має той же знак, що й операнд в
. Після цього вилучення зі стека і кут заміщує два операнди у вершині стека. Результат має той же знак, що й операнд в  і величину
і величину  . Термін “частковий арктангенс” успадкований від процесорів 8087 і 80287, в яких були обмеження на значення в
. Термін “частковий арктангенс” успадкований від процесорів 8087 і 80287, в яких були обмеження на значення в  їх відношення, спрощує обчислення інших тригонометричних функцій. Наприклад,
їх відношення, спрощує обчислення інших тригонометричних функцій. Наприклад,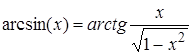 , (38.1)
, (38.1) . (38.2)
. (38.2) .
.


 .
. . Маємо
. Маємо .
. , то одержуємо
, то одержуємо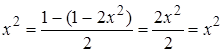 . Одержана рівність підтверджує правильність співвідношення (38.1).
. Одержана рівність підтверджує правильність співвідношення (38.1).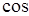

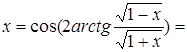
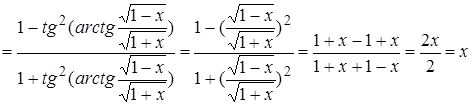 .
. , число мінут – на
, число мінут – на  , число секунд – на
, число секунд – на  і знайдені добутки додати.
і знайдені добутки додати.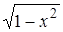 і записати його в стек.
і записати його в стек. і записати його в стек.
і записати його в стек.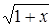 і записати його в стек.
і записати його в стек. , косинуса –
, косинуса –  , а також синуса косинуса –
, а також синуса косинуса –  . Для цих команд
. Для цих команд  використовується для обчислення виразу
використовується для обчислення виразу  . Значення
. Значення  . Якщо операнд поза припустимим діапазоном, результат невизначений. Віднімання 1 пов’язано з точністю обчислень, коли значення
. Якщо операнд поза припустимим діапазоном, результат невизначений. Віднімання 1 пов’язано з точністю обчислень, коли значення  , то це можна зробити за формулою
, то це можна зробити за формулою . (38.3)
. (38.3) можна обчислити за допомогою команди
можна обчислити за допомогою команди  , яка обчислює двійковий логарифм числа
, яка обчислює двійковий логарифм числа 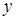 . Аргумент
. Аргумент  .
.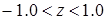 , то далі легко обчислити
, то далі легко обчислити 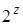 , застосувавши команду
, застосувавши команду 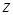 не з даного діапазону, потрібно виконати додаткові обчислення за наступним алгоритмом:
не з даного діапазону, потрібно виконати додаткові обчислення за наступним алгоритмом: і одержимо в
і одержимо в  , а порядок числа в форматі числа РТ в регістрі
, а порядок числа в форматі числа РТ в регістрі  , де
, де 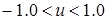 – вміст регістра
– вміст регістра  , де
, де  – істинний порядок
– істинний порядок  ;
; ;
; , в
, в 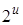 ;
; , в
, в  .
. – обчислює значення виразу:
– обчислює значення виразу: 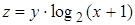 . Значення
. Значення  , значення
, значення  . Результат на місці
. Результат на місці 


