
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм кодирования кодом ХэммингаСодержание книги Поиск на нашем сайте
Пусть задано информационное слово С закодировать кодом Хэмминга (7,4). Код Хэмминга (7,4) задан порождающей матрицей вида (3). Комбинация на выходе кодера получается из соотношения:
Проверочные символы для кода Хэмминга (7,4) формируются в соответствии с приведенными выражениями:
При записи кодовой комбинации на выходе кодера первые k символов кода
произведению принятого кодового слова на транспонированную проверочную матрицу. Если кодовое слово будет принято без искажений, то синдром будет равен нулю,
т.е. S 000. Если жекакой-либосимвол будет принят с искажением, то синдром совпадает со столбцом проверочной матрицы и укажет на номер разряда (символа в кодовом слове), который принят с ошибкой. Для исправления ошибки нужно к символу разряда в котором произошла ошибка прибавить единицу по модулю два.
Под мажоритарными групповыми кодами принято понимать такие групповыми коды, которые позволяют при декодировании использовать принцип решения по большинству (мажоритарный принцип). При декодировании кодом Хэмминга используется синдромное декодирование.
Свойство проверочной матрицы: произведение закодированного слова (разрешенной кодовой комбинации) на транспонированную проверочную матрицу равно нуль-вектору: b 0, b 1, b 2,..., bk 1, a 0, a 1,..., ar 1 Проверочная и порождающая матрицы связаны выражением:
В обобщенном виде, алгоритм исправления ошибок включает в себя три этапа: вычисление синдрома; синтез вектора ошибок; исправление ошибки. Рассмотрим этапы более подробно.
Вычисление синдрома. Для кода Хэмминга (7,4) синдромом будет 3-хразрядная кодовая комбинация:
где С H T – транспонированная проверочная матрица. Согласно правилу умножения вектора на матрицу элементы синдрома будут определяться выражениями: S 0 b 1 b 2 b 3 a 0, S 1 b 0 b 2 b 3 a 1, S 2 b 0 b 1 b 3 a 2. Если кодовое слово будет принято без искажений, то синдром будет равен нулю, т.е. S 000. Если же какой-либосимвол будет принят с искажением, то синдром укажет на номер элемента в кодовом слове, который принят ошибочно. Вектор ошибок это кодовая комбинация, которая ставится в соответствие синдрому и содержит единицу в том разряде, где произошла ошибка, и нули во всех остальных разрядах. Составим таблицу соответствия синдрома и вектора ошибок: Таблица 1 Таблица соответствия вектора ошибки синдрому сообщения
35.
На основании данной таблицы получим элементы вектора ошибок: e 0 S 0 S 1 S 2, e 1 S 0 S 1 S 2, e 2 S 0 S 1 S 2, e 3 S 0 S 1 S 2. Например, с ошибкой был принят символ b 2, в этом случае синдром будет равен S 110, а это третий столбец в проверочной матрице, которому соответствует вектор ошибок e 0010. Исправить ошибку довольно легко, для этого нужно произвести поразрядное сложение по модулю два принятого кодового слова и синтезированного вектора ошибок. Пример. 36. Пусть принята кодовая комбинация C
37. 6
38. Пример. 40. Введем в принятую кодовую комбинацию, ошибку во втором разряде, т.е. 41. C 42. Произведем вычисление синдрома:
43. матрицы, в таблице соответствия (табл. 2.1) это третья строка следовательно вектор ошибок примет вид e 0100. 44. Запишем процесс исправления ошибки: 45. С e 0100 – вектор ошибок, С 1010 – исправленная информационная кодовая комбинация. Схема декодера для выбранного кода Хэмминга (рис. 3) строится по известной проверочной матрице H с использованием метода синдромного декодирования. В состав структурной схемы декодера кода Хэмминга (7,4) входят: блок вычисления синдрома; формирователь вектора ошибок; выходные сумматоры по модулю два, в которых происходит процесс исправления ошибок.
Блок вычисления синдрома
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 578; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.231.160 (0.009 с.) |

 b 0 b 1 b 2 b 3 1010, которое нужно
b 0 b 1 b 2 b 3 1010, которое нужно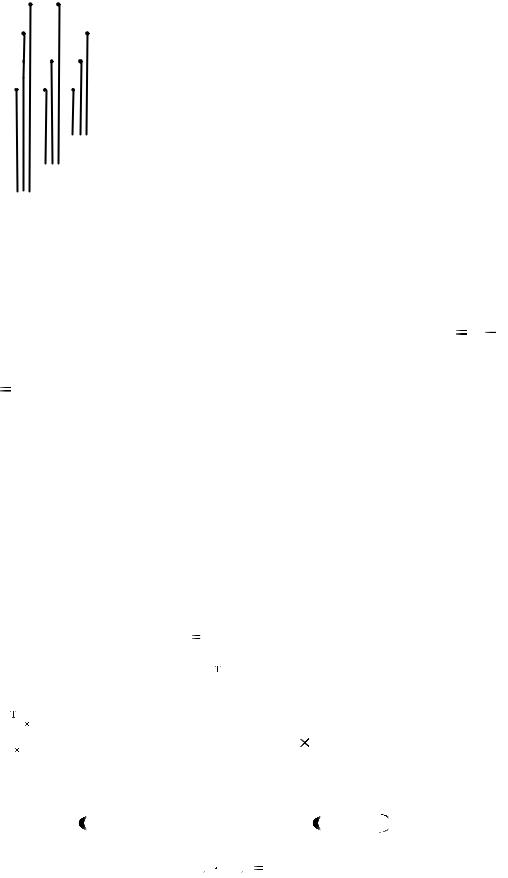
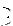 H T
H T 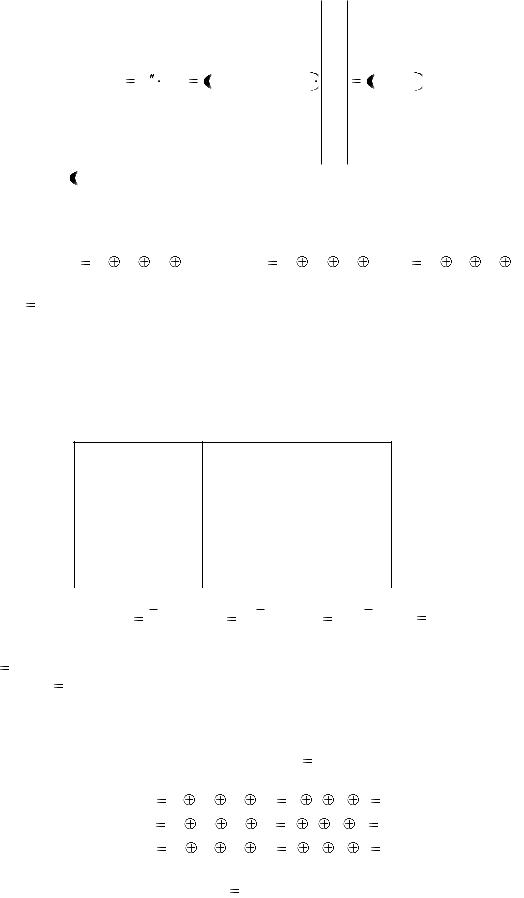
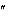
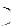 – принятое сообщение;
– принятое сообщение;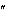 1010 _101 без ошибки. Произведем вычисление синдрома:
1010 _101 без ошибки. Произведем вычисление синдрома: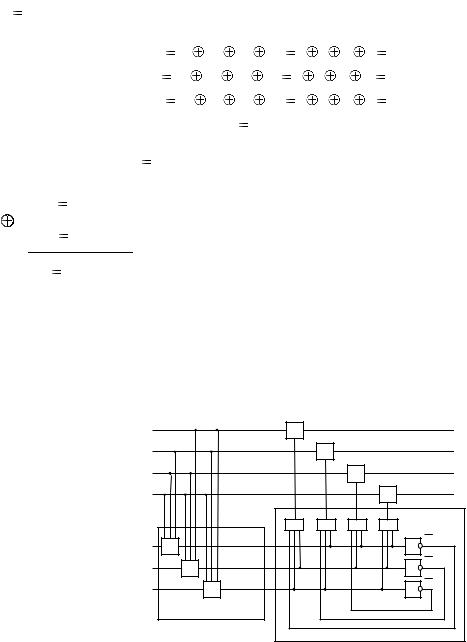
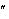 1110 – информационные символы принятой кодовой комбинации,
1110 – информационные символы принятой кодовой комбинации,


