
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Надежность программных комплексовСодержание книги Поиск на нашем сайте
НАДЕЖНОСТЬ ПРОГРАММНЫХ КОМПЛЕКСОВ Пример 2. На условиях примера 1, определить вероятность безошибочной работы программы в течение 90 суток. Решение. Вероятность безошибочной работы программы в течение 90 суток, в соответствии с выражением (5.3), равно
Пример 3. Определить первоначальное количество возможных ошибок в программе, содержащей 2 000 командных строк, если в течение первых 60 суток эксплуатации было обнаружено 2 ошибки, а за последующие 40 суток была обнаружена одна ошибка. Определить T0 – среднее время безошибочной работы, соответствующее первому и второму периоду эксплуатации программы и коэффициент пропорциональности. Решение. В соответствии с выражением (5.8), находим первоначальное количество возможных ошибок в программе:
При этом среднее время безошибочной работы, соответствующее первому и второму периоду эксплуатации программы определяется выражением:
Коэффициент пропорциональности находится по формуле (5.9):
Вторая модель, как и первая, основана на допущении об экспоненциальном распределении вероятности безошибочной работы программного комплекса. Предполагается, что частота появления ошибок пропорциональна числу остаточных ошибок, т. е.
где t – интервал времени между i -й и (i -1)-й обнаруженными ошибками. С помощью формулы (5.10) можно найти вероятность безошибочной работы:
и среднее время безошибочной работы:
Пример 4. Интервал времени между 3-й и 4-й обнаруженными ошибками в программе, состоящей из 2 000 командных строк, был равен 50 суткам. Коэффициент пропорциональности равен 0,005. Общее количество ошибок в начале эксплуатации составляет 15 штук. Определить частоту появления ошибок, вероятность безошибочной работы и среднее время безошибочной работы. Решение. Частота появления ошибок определяется из выражения (5.10):
Вероятность безошибочной работы можно найти из выражения (5.11):
Среднее время безошибочной работы:
Третья модель основана на допущении о том, что частота появления ошибок пропорциональна числу остаточных ошибок и времени отладки программы, т. е.
где t1 –промежуток времени между(i-1)-й и i -й ошибками. Вероятность безошибочной работы равна:
Среднее время безошибочной работы определяется по формуле:
Существуют доводы как за, так и против принятия допущения о том, что частота появления ошибок пропорциональна времени отладки программы. Истинную ценность той или иной модели можно измерить по её прогнозирующей способности. В большинстве случаев, обсуждение относительной ценности моделей обычно основывается на интуиции и проверке логической непротиворечивости. Тот факт, что число попыток экспериментально проверить эти модели невелико, объясняется отсутствием необходимых данных об ошибках в программах или противоречивостью имеющихся данных. Из всех рассмотренных моделей, наилучшие прогнозы остаточных ошибок для крупномасштабных разработок программ или проектов с продолжительным периодом отладки даёт третья модель. Следует иметь в виду, что, хотя это сравнительное исследование позволило получить некоторые полезные результаты, необходимы новые исследования такого рода. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Возможно ли повышение надежности программных комплексов путем резервирования? Пояснить. 2. Как определить интенсивность отказов в течение интервалов времени t 3. Как определить вероятность безошибочной работы в течение интервалов времени t с использованием первой и второй математической модели надежности программных комплексов? 4. Как определить среднее время безошибочной работы программы с использованием первой и второй математической модели надежности программных комплексов? 5. Критерии надежности программных комплексов. 6. Факторы, влияющие на надежность программных комплексов? НАДЕЖНОСТЬ ПРОГРАММНЫХ КОМПЛЕКСОВ
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 581; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.216.107 (0.009 с.) |

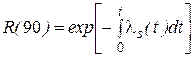 =
= 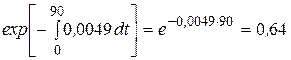 .
.
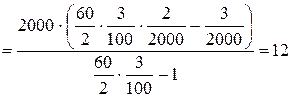 .
.
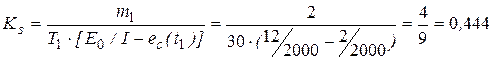 .
.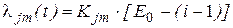 , (5.10)
, (5.10)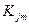 – коэффициент пропорциональности;
– коэффициент пропорциональности;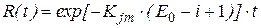 , (5.11)
, (5.11)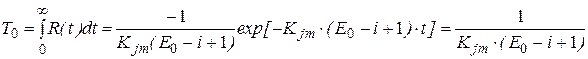 . (5.12)
. (5.12)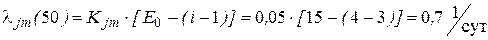 .
.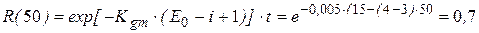 .
.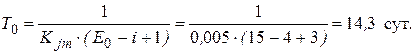
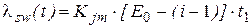 , (5.13)
, (5.13)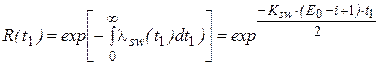 . (5.14)
. (5.14)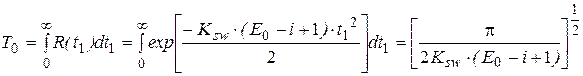 . (5.15)
. (5.15)


