
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика статистической обработки результатов многократных прямых измерений.Содержание книги
Поиск на нашем сайте
Главной особенностью измерительного эксперимента, проводимого с использованием статистической обработки полученных данных, является получение и использование большого объема апостериорной измерительной информации. Рассмотрим группу из n независимых результатов наблюдений случайной величины Поскольку число наблюдений в группе, на основании которых вычислено среднее арифметическое Теория показывает, что если рассеяние результатов наблюдений в группе подчиняется нормальному закону, то и их среднее арифметическое тоже подчиняется нормальному закону распределения при достаточно большом числе наблюдений (п > 50). Отсюда следует, что при одинаковой доверительной вероятности, доверительный интервал среднего арифметического в Правила обработки результатов измерения с многократными наблюдениями учитывают следующие факторы: обрабатывается ограниченная группа из п наблюдений; результаты наблюдений Обработку ряда наблюдений следует выполнять в соответствии с методикой по ГОСТ 8.207-76 «Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений». При выполнении этой последовательности действий руководствуются следующими правилами: - проверку гипотезы о принадлежности результатов наблюдений нормальному распределению проводят с уровнем значимости - при определении доверительных границ погрешности результата измерения доверительную вероятность Р принимают равной 0.95.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 292; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.55.237 (0.006 с.) |

 , подчиняющейся нормальному распределению. Оценка рассеяния единичных результатов наблюдений в группе относительно среднего их значения
, подчиняющейся нормальному распределению. Оценка рассеяния единичных результатов наблюдений в группе относительно среднего их значения 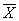 вычисляется по формуле 2.2.
вычисляется по формуле 2.2.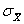 (см. формулу 2.4). Среднее квадратическое отклонение
(см. формулу 2.4). Среднее квадратическое отклонение  раз уже доверительного интервала результата наблюдений. Теоретически при
раз уже доверительного интервала результата наблюдений. Теоретически при  случайную погрешность результата измерения можно было бы свести к нулю. Однако это невозможно, и стремиться беспредельно уменьшать случайную погрешность результата измерения не имеет смысла, так как рано или поздно определяющим становится не рассеяние среднего арифметического, а недостоверность поправок на систематическую погрешность (неисключенная систематическая погрешность).
случайную погрешность результата измерения можно было бы свести к нулю. Однако это невозможно, и стремиться беспредельно уменьшать случайную погрешность результата измерения не имеет смысла, так как рано или поздно определяющим становится не рассеяние среднего арифметического, а недостоверность поправок на систематическую погрешность (неисключенная систематическая погрешность). могут содержать систематическую погрешность; в группе наблюдений могут встречаться грубые погрешности; распределение случайных погрешностей может отличаться от нормального. При этом могут быть использованы различные процедуры обработки результатов наблюдений.
могут содержать систематическую погрешность; в группе наблюдений могут встречаться грубые погрешности; распределение случайных погрешностей может отличаться от нормального. При этом могут быть использованы различные процедуры обработки результатов наблюдений. , выбираемым в диапазоне от 0.02 до 0.1;
, выбираемым в диапазоне от 0.02 до 0.1;


