
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии оптимизации моделей в машиностроении.Содержание книги
Поиск на нашем сайте
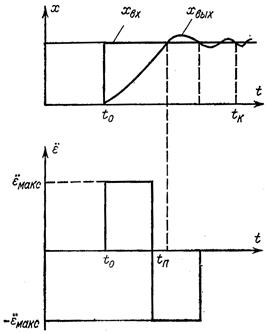
Одним из самых важных и в то же время далёких от удовлетворительного решения является вопрос о критериях оптимизации. Достаточно грамотно формулировать критерии управления можно с помощью прагматики – науки, которая занимается определением целей и задач управления, изучением значения и ценности результатов поведения, движения, развития и управления системами. От чисто качественного, неформализованного характера методы прагматики отличаются более высоким уровнем формализации с помощью семиотики и математической лингвистики: Семиотика (от греч.-знак) – комплекс научных теорий, изучающих свойства знаковых систем, т.е. систем конкретных или абстрактных объектов (их называют знаками), с каждым из которых определённым образом сопоставлено некоторое значение. · Математическая лингвистика – прикладная математическая дисциплина, основной задачей которой является разработка точных методов исследования естественных языков. В ней широко используются методы теории алгоритмов, теории автоматов и алгебры. Эта наука включает в себя три основных раздела: 1) разработка и изучение способов описания структуры отрезков речи; 2)изучение формального строения лингвистически значимых отношений и классификаций на множествах языковых объектов; 3)теория формальных грамматик. Эти разделы отвечают трём аспектам формального описания языка. Выбор конкретного критерия оптимизации зависит от конструктора системы или технолога, и в этом содержится элемент нестрогости. На практике всё чаще используют типовые критерии, которые становятся общепринятыми и заносятся в технические задания. При решении задач оптимизации необходимо различать понятия функции и функционала. В математике понятие функционала является дальнейшим обобщением понятия функции. Не очень строго функционал можно определить как функцию от функции, т.е. функцию, в которой в качестве независимой переменной выступает функция. Рассмотрим наиболее распространённые виды критериев оптимизации и области их применения: 1. Критерий среднего квадрата ошибки. Применяется при оценке качества работы автоматической системы регулирования (АСР) и при решении математических задач оптимизации. 2. Интегральный критерий. Используется для определения параметров АСР, оптимальной в переходном процессе. 3. Критерий максимального быстродействия. При определении параметров АСР в режиме переходного процесса часто используют критерий оптимальности, обеспечивающий её быстродействие, т.е. переходный процесс должен заканчиваться в минимальное время. Выполнение этого требования повышает качество обработки деталей при использовании копировальных следящих систем. В этом случае следящая система должна отрабатывать входной сигнал с отсутствием (в идеале) колебательности 4. Критерий минимума стоимости. В данном случае рассматривается функционал, определяющий стоимость функционирования совокупности систем массового обслуживания (или сети массового обслуживания) в единицу времени: Случайность потока заявок и времени их обслуживания обуславливают какое-то среднее число простаивающих ячеек обслуживания или ожидающих заявок. Для оптимизации работы системы массового обслуживания необходимо, чтобы Такую модель и критерий можно использовать в машиностроении в различных ситуациях, например при организации службы по ремонту оборудования. В этом случае ячейку обслуживания представляет ремонтная бригада, а заявку – отказы оборудования. Минимум функционала означает оптимальный выбор числа бригад, основанный Рис. Интерпретация критериев оптимизации: а – к определению ошибки АСР; б – оценка качества работы АСР по величинам дисперсии или модуля ошибки; в – интегральный критерий качества; г – оптимальная по быстродействию система; д – пример сетевого графика
5. Критерий минимума критического времени выполнения работы. Этот критерий используется при оптимизации сетевых моделей планирования и управления производственным процессом. Примером может служить процесс конструкторско-технологической подготовки производства для выпуска новой продукции и другие ситуации, когда выполнение поставленной задачи сводится к выполнению определённого количества работ и возникает вопрос о критическом пути. 6. Минимаксный критерий. Этот критерий широко используется для определения оптимальной стратегии принятия решений при наличии конфликтной ситуации, что для условий производства означает наличие конкуренции в различных сферах (сбыт, обслуживание и т.д.). В такой ситуации интересы двух сторон противоположны, так как выигрыш одной стороны означает проигрыш другой. Поэтому приходится выбирать среди худших для себя стратегий конкурента (противника) наименее худшую, т.е. брать максимум по множеству стратегий противника и минимум по собственным стратегиям
8.2.. Классификация методов оптимизации.
Исходя из возможности нескольких подходов к классификации, следует различать методы определения экстремума функции и функционала (рис.). Являясь частным случаем функционала, функция отличается более простыми методами отыскания экстремума. Современная практика оптимизации производственных процессов требует применения как аналитических, так и численных методов поиска экстремума. Преимущество аналитических методов заключается в возможности определения качественной картины поведения оптимальной системы при изменении её параметров и структуры. Применение численных методов обеспечивает получение конкретных числовых значений параметров управления производственным процессом. Особое место занимают человеко-машинные методы оптимизации, использующие возможности работы оператора в режиме диалога с ЭВМ. Это даёт возможность повторять вычисления при разных условиях, использовать аналитические методы, представленные в виде стандартных программных блоков и, что самое важное, оперативно включать в процедуру отыскания оптимального решения интеллектуальные способности человека. Весьма важно, что при таком способе оптимизации исходный критерий оптимальности может быть нестрого математически формализован в виде функции или функционала. Так, он может состоять из нескольких положений, сформулированных достаточно чётко на словесном, содержательном уровне, что при наличии диалога человек - машина вполне допустимо. Методы отыскания экстремума функции получили широкое развитие из-за вычислительных трудностей решения алгебраических уравнений вида
особенно при наличии ограничений на переменные Увеличение числа переменных Во многих областях практики, в том числе и в машиностроении, возникают задачи оптимизации применяемых решений, имеющих следующие характерные черты: · показатель эффективности · ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств. Такие задачи составляют круг задач линейного программирования.
Вопросы для самопроверки Рекомендуемая литература
Раздел 6: «Современные технологии математического моделирования процессов, средств и систем машиностроительных производств» (2 часа)
Лекция 8. «Моделирование систем машиностроения с применением элементов искусственного интеллекта.» (1 час) (1 час) План лекции: 8.3. Основные понятия и определения. Основы теории нечетких множеств. 8.3. Основные понятия и определения. Основы теории нечетких множеств. Решение актуальных технических проблем, создание сложных технических объектов, включающее моделирование и управление, невозможно без привлечения методов искусственного интеллекта, направленного на решение определенного класса задач при их специфической алгоритмизации, составляющей класс генетических алгоритмов. В последнее время все более широко распространяется построение и исследование моделей поведения сложных технических объектов и способов управления ими на основе имитации реализованных природой механизмов в живых существах, т.е. происходит биологизация процессов моделирования и управления [17]. Возможно и совместное применение различных моделей и методов при обработке информации об одном и том же объекте – в этом состоит сущность гибридизации. Согласие с тем, что любая сколь угодно сложная искусственная модель реального объекта всегда примитивнее и проще оригинала и лишь многоаспектное его изучение с последующей интеграцией получаемых результатов позволит обрести необходимые знания или приблизиться к оптимальному решению, представляет собой основу парадигмы (греч.:paradeima – пример, образец. П.– строго научная теория, воплощенная в системе понятий, выражающих существенные черты действительности) такого подхода. Можно с высокой степенью уверенности констатировать, что биологизация и гибридизация составляют основные тенденции развития кибернетики в начале третьего тысячелетия. Обучение – способность системы улучшать свое поведение в будущем, основываясь на прошлой экспериментальной информации о результатах взаимодействия с окружающей средой. Самообучение – обучение системы без внешней корректировки, т.е. без указаний «учителя». Интеллектуальная система управления (ИСУ) – такая, в которой знания о неизвестных характеристиках управляемого объекта и окружающей среды формируются в процессе обучения и адаптации, а полученная при этом информация используется в процессе автоматического принятия решений для улучшения качества управления. Необходимый признак ИСУ – наличие базы знаний, содержащей сведения, модели и правила, позволяющие уточнить поставленную задачу управления и выбрать рациональный способ ее решения. Наибольшее распространение при проектировании ИСУ получили методы интеллектуального управления (ИУ), которые относятся к четырем классам [4]: 1) экспертные системы; 2) нечеткие системы; 3) нейронные сети; 4) генетические алгоритмы. Различным уровням интеллектуальности соответствуют ИСУ, интеллектуальные «в большом» и «в малом». Чем же они отличаются? Интеллектуальные «в большом» – организованы и функционируют в соответствии с пятью принципами: · взаимодействие с реальным внешним миром через информационные каналы связи; · принципиальная открытость системы с целью повышения интеллектуальности и совершенствования собственного поведения; · наличие механизмов прогноза изменения внешнего мира и собственного поведения системы в изменяющихся условиях; · наличие многоуровневой иерархической структуры, соответствующей правилу повышения интеллектуальности и снижения требований к точности моделей по мере повышения уровня иерархии в системе (и наоборот); · сохраняемость функционирования (возможно, с некоторой потерей качества) при разрыве связей или потере управляющих воздействий от высших уровней иерархии. Интеллектуальные «в малом» не удовлетворяют перечисленным принципам, но используют при функционировании знания (можно в виде правил) как средство преодоления неопределенности входной информации, описания управляемого объекта или его поведения. При проектировании ИСУ наибольшее распространение получили методы ИУ, относящиеся к следующим четырем классам: · экспертные системы; · нечеткие регуляторы; · нейронные сети; · генетические алгоритмы. В случае четких множеств традиционный способ представления элемента
В нечетких множествах элемент Степень принадлежности элемента Конкретное значение функции принадлежности называется степенью, или коэффициентом принадлежности. Степень принадлежности может быть определена в виде функциональной зависимости или дискретно – путем задания конечной последовательности значений
Теория нечетких множеств допускает, помимо переменных цифрового типа, существование лингвистических переменных с приписываемыми им значениями. Для нечетких множеств, являющихся обобщением обычных множеств, существует ряд математических операций, которые являются обобщением аналогичных операций, выполняемых на четких множествах. Среди прочих, к ним относятся следующие: 1. Логическая сумма множеств
2. Логическое произведение множеств
Здесь знаки 3. Отрицание множества
Отрицание нечеткого множества в отличие от обычных четких множеств дает непустое множество, состоящее из элементов, функции принадлежности которых также определены на интервале 4. Равенство нечетких множеств 5. Операции концентрации
Часто выполняется при действиях с лингвистической переменной, в которых она отождествляется с интенсификатором «очень». 6. Операция растяжения
Лингвистическое значение этой операции формулируется как «примерно» или «приблизительно». 7. Ограниченная сумма
8. Нормализация нечеткого множества
Нечеткое множество Свойства ассоциативности, коммутативности и дистрибутивности операций, определенных на нечетких множествах, понимаются следующим образом: v ассоциативность: v коммутативность: v дистрибутивность: Для нечетких множеств корректны следующие выражения:
т.е. в отличие от обычных множеств, логическое произведение нечеткого множества и его отрицания не обязательно образуют пустое множество, а их логическая сумма не обязательно образует полное множество Важным для практики является вопрос о степени нечеткости нечетких множеств. Для ее определения введено понятие меры нечеткости, сводящейся к измерению уровня различия между множеством В соответствии с мерой Р. Егера степень нечеткости множества
где Значения
Рекомендуемая литература
План лекции: 9.1. Элементы нейросетевого моделирования процессов в технических объектах и системах. 9.2. Генетические алгоритмы и их применение в моделировании технических систем.
|
||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.112.210 (0.012 с.) |

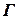 =min.
=min. на определённой статистике потока отказов оборудования.
на определённой статистике потока отказов оборудования. а)
а)
 в)
в)
 д)
д)
 б)
б)
 г)
г)
 Методы оптимизации исторически развивались независимо с использованием различных концепций, математических аппаратов и т.д., что объясняет определённую сложность их классификации. Рассмотрим классификацию методов оптимизации в трактовке работы которая, хотя и носит условный характер, даёт возможность ознакомиться с их особенностями и областями применения.
Методы оптимизации исторически развивались независимо с использованием различных концепций, математических аппаратов и т.д., что объясняет определённую сложность их классификации. Рассмотрим классификацию методов оптимизации в трактовке работы которая, хотя и носит условный характер, даёт возможность ознакомиться с их особенностями и областями применения. , j=1,2,…n,
, j=1,2,…n,
 .
. представляет собой линейную функцию от элементов решения
представляет собой линейную функцию от элементов решения 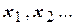 ;
;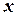 множества
множества  состоит в применении характеристической функции
состоит в применении характеристической функции  . Для четких множеств имеем:
. Для четких множеств имеем:

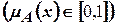 , которая представляет собой обобщение характеристической функции. Ее значения являются рациональными числами из интервала
, которая представляет собой обобщение характеристической функции. Ее значения являются рациональными числами из интервала  . Причем 0 означает отсутствие принадлежности, а 1 – полную принадлежность к множеству
. Причем 0 означает отсутствие принадлежности, а 1 – полную принадлежность к множеству 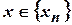 в виде:
в виде:
 .
. .
.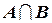 .
. .
. и
и  обозначают соответственно операторы
обозначают соответственно операторы  и
и  .
.
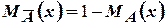 .
. и
и  возможно, когда для всех элементов
возможно, когда для всех элементов  обоих множеств выполняется условие
обоих множеств выполняется условие  .
.
 .
.
 .
. , разность
, разность  и произведение
и произведение  двух нечетких множеств
двух нечетких множеств  определяются соответственно выражениями:
определяются соответственно выражениями: ,
,  ,
, 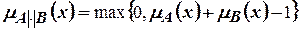 .
. определяется соотношением
определяется соотношением .
. , если для всех элементов выполняется неравенство
, если для всех элементов выполняется неравенство  .
. ;
; (за исключением ограниченной разности);
(за исключением ограниченной разности); , где операторы
, где операторы  и
и  обозначают любую определенную выше операцию на нечетких множествах.
обозначают любую определенную выше операцию на нечетких множествах. Æ;
Æ; ,
,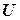 .
. , обозначаемая
, обозначаемая  , определяется по формуле:
, определяется по формуле: ,
, – мера расстояния между множествами
– мера расстояния между множествами 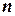 элементов.
элементов. и
и  соответствуют метрикам Хемминга и Евклида, и искомые меры расстояния определяются по формулам:
соответствуют метрикам Хемминга и Евклида, и искомые меры расстояния определяются по формулам: ;
;  . Вопросы для самопроверки
. Вопросы для самопроверки


