
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторный практикум по физике.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСТЕТ» ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ФИЗИКЕ. МЕХАНИКА Методические указания к лабораторным работам ОМСК 2008 Составители В.Н.Иванов, к.ф.-м.н., Г.П.Иванова, Т.Н.Кондратьева, О.В.Кропотин, к.т.н., О.В.Лях, В.О.Нижникова, О.Ю.Павловская, А.Г.Туровец, к.ф.-м.н. Данные методические указания содержат описание семи лабораторных работ. Указание к каждой работе содержит краткие теоретические сведения, необходимые для правильного выполнения лабораторной работы, описание лабораторной установки, порядок выполнения лабораторной работы, правила обработки результатов и контрольные вопросы.
Печатается по решению редакционно-издательского совета ОмГТУ
ЛАБОРАТОРНАЯ РАБОТА 11 – 1 МАЯТНИК МАКСВЕЛЛА
Цель работы: изучение движения маятника Максвелла и определение его момента инерции. Приборы и принадлежности: лабораторная установка «Маятник Максвелла», секундомер.
Краткая теория
Если, накрутив нити на концы стержня, поднять маятник на некоторую высоту
Если потерями энергии пренебречь, то можно считать, что во время движения (и при спуске, и при подъеме) на маятник действуют (рис.2) только две постоянные по модулю и направлению силы . В лабораторной работе экспериментально проверяется равноускоренный характер движения маятника Максвелла и определяется его момент инерции.
Определение момента инерции маятника Максвелла основано на использовании закона сохранения механической энергии. Если пренебречь потерями энергии, то по закону сохранения механической энергии
Здесь Решая уравнение (1) относительно
Поскольку движение маятника равноускоренное,
где
где Подставляя (4) и (3) в (2), получаем формулу для определения момента инерции маятника Максвелла:
Выражение (5) содержит величины, которые можно определить экспериментально.
Момент инерции маятника Максвелла можно вычислить также теоретически, используя соотношение:
где
Порядок выполнения работы
1. Ознакомиться с устройством лабораторной установки. Записать в отчет цену деления измерительной шкалы на вертикальной стойке и точность секундомера. 2. Убедиться, что в состоянии равновесия ось маятника занимает горизонтальное положение. При необходимости подтянуть нить в сторону одного из концов стержня. 3. По шкале на вертикальной стойке определить по нижнему краю диска положение маятника 4. Аккуратно накручивая нить на концы стержня (виток к витку, в направлении от концов стержня), поднять маятник в верхнее положение. Отпустить маятник и пронаблюдать за его движением. Обратить внимание на изменение высоты подъёма. 5. Снова поднять маятник в верхнее положение, заметить по шкале его положение Замечание! Если наматывание нитей при движении маятника вверх будет происходить несимметрично, с перекосом оси, или в направлении к концам стержня, маятник необходимо остановить и проделать опыт снова. 6. Повторить действия согласно пункту «5», варьируя значения
ЛАБОРАТОРНАЯ РАБОТА 11-3
ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Цель работы: проверка основного закона динамики вращательного движения твердого тела с помощью маятника Обербека. Приборы и принадлежности: лабораторная установка «Маятник Обербека», набор грузов, секундомер, штангенциркуль, масштабная линейка.
Краткая теория
Вращение твердого тела постоянной массы вокруг неподвижной оси подчиняется основному закону динамики вращательного движения
где
Экспериментальную проверку этого закона можно провести на приборе, называемом маятником Обербека. На рис.1 схематически изображен маятник, используемый в данной работе. Он представляет собой вал А, на котором радиально закреплены два металлических стержня С. На стержни симметрично на расстоянии
Если, намотав нить на вал, поднять груз Чтобы убедиться в справедливости основного закона динамики вращательного движения, выведем формулы, дающие возможность экспериментально определить физические величины, входящие в (1).
Вращение маятника вызывается силой натяжения
где По третьему закону Ньютона Согласно второму закону Ньютона, записанному в проекциях на направление движения:
Подстановка (с учетом равенства
Ускорение
Подставляя (4) в (3) и учитывая, что
В формулу (5) входят экспериментально определяемые величины.
Угловое ускорение маятника
Если нет проскальзывания нити, то
В формулу (7) входят величины, значения которых определяются экспериментально.
Основной закон динамики вращательного движения (1) позволяет по известным значениям момента силы и углового ускорения определить момент инерции маятника Обербека относительно оси вращения:
Проверка основного закона динамики вращательного движения в данной лабораторной работе состоит из двух частей.
1. Проверка прямой пропорциональности углового ускорения маятника результирующему моменту приложенных сил.
Если момент инерции маятника не изменяется (
Примечание. Момент силы натяжения, действующий на маятник, можно изменить, меняя массу груза, подвешиваемого к нити (см. формулу (5)).
ЛАБОРАТОРНАЯ РАБОТА 11-4
Краткая теория
Формула (1) является приближённой. Для определения точного значения момента инерции твердого тела с непрерывным распределением массы следует воспользоваться интегральным представлением
где
Используя формулу (2), достаточно просто вычислить моменты инерции тел, имеющих правильную геометрическую форму, относительно осей симметрии, проходящих через центр масс. Например, моменты инерции прямоугольного параллелепипеда относительно осей симметрии (рис. 2) выражаются формулами:
где
Моменты инерции твердых тел можно определить и экспериментальными методами, одним из которых является метод крутильных колебаний.
где Система, совершающая крутильные колебания, называется крутильным маятником.
В лабораторной работе используется крутильный маятник, представляющий собой металлическую рамку с известным моментом инерции Исследуемое твердое тело жестко закрепляется в рамке. Если вывести такой маятник из положения равновесия, то он будет совершать крутильные колебания, период
где Если колеблется свободная рамка (без тела), то ее период колебаний равен:
Совместное решение уравнений (5) и (6) позволяет записать для
Таким образом, для определения момента инерции исследуемого тела необходимо знать момент инерции свободной рамки
Примечание 1. В качестве исследуемого тела в работе предлагается прямоугольный параллелепипед.
Примечание 2. Момент инерции свободной рамки лабораторной установки равен
Примечание 3. Для повышения точности измерений при нахождении периодов крутильных колебаний
где
Порядок выполнения работы
1. Ознакомиться с устройством лабораторной установки. Записать в отчет точность секундомера и штангенциркуля. 2. Повернуть рамку на угол 3. Закрепить параллелепипед в рамке относительно одной из осей симметрии (по указанию преподавателя) и, аналогично описанному в п.2, измерить не менее трех раз время 4. Снять параллелепипед и при помощи штангенциркуля определить его размеры
ЛАБОРАТОРНАЯ РАБОТА 11-5
СОУДАРЕНИЕ ШАРОВ
Цель работы: изучение удара шаров, определение коэффициента восстановления скорости при ударе. Приборы и принадлежности: экспериментальная установка, набор шаров. Краткая теория Ударом называется кратковременное взаимодействие тел, при котором за малый промежуток времени ( Прямая, проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения, называется линией удара. Если линия удара проходит через центры масс соударяющихся тел, то удар называется центральным. Различают два предельных случая удара: абсолютно неупругий и абсолютно упругий. Абсолютно неупругий удар – это столкновение тел, после которого взаимодействующие тела движутся как единое целое или останавливаются. При таком ударе механическая энергия соударяющихся тел частично или полностью переходит во внутреннюю. Тела претерпевают деформации, которые являются неупругими, и нагреваются. При абсолютно неупругом ударе выполняется закон сохранения импульса. Абсолютно упругий удар – столкновение, при котором механическая энергия соударяющихся тел не преобразуется в другие виды энергии. В процессе такого удара тела также деформируются, но деформации являются упругими. После соударения тела движутся с различными скоростями. При абсолютно упругом ударе выполняются законы сохранения импульса и механической энергии. Абсолютно упругий удар – идеализация. При столкновении реальных тел механическая энергия к концу взаимодействия восстанавливается лишь частично, вследствие потерь на образование остаточных деформаций и нагревание. Степень упругости удара характеризует величина При центральном ударе
где
В данной лабораторной работе изучается центральный удар двух металлических шаров и определяется коэффициент восстановления скорости.
Пусть два шара одинаковой массы По закону сохранения механической энергии
где
Высоту
Подставляя (4) в (3), получим
Аналогичные формулы можно получить для
где Подставив в выражение (1) значения
Таким образом, для определения коэффициента восстановления скорости необходимо при заданном угле
Порядок выполнения работы
1. Ознакомиться с устройством лабораторной установки. Определить цену деления измерительных шкал, записать в отчет. 2. Удостовериться, что шары соприкасаются и их центры находятся на одном уровне. При необходимости произвести центровку. По измерительным шкалам заметить начальные положения шаров. 3. Отклонить правый шар на угол 10-12 градусов от начального положения и зафиксировать его электромагнитом, нажав кнопу "Сброс". Значение угла отклонения 4. Убедиться, что левый шар находится в состоянии покоя. Нажать кнопку "Пуск" и по измерительным шкалам визуально определить углы отклонения правого ( Внимание! Углы отклонения шаров после соударения определять относительно их начальных положений! 5. Опыт проделать еще 4 раза, повторяя действия п.п. 3 – 4 при одном и том же угле
ЛАБОРАТОРНАЯ РАБОТА 11 – 6 МЕТОДОМ НАКЛОННОГО МАЯТНИКА
Цель работы: изучение силы трения качения и определение коэффициента трения качения методом наклонного маятника. Приборы и принадлежности: лабораторная установка.
Краткая теория
Строгая теория трения качения выходит за рамки курса общей физики. Однако в первом приближении можно считать, что трение качения является результатом деформаций тела и поверхности при их контакте. На поверхности возникает углубление под телом и "валик" перед ним. В результате тело соприкасается с поверхностью не в одной точке, а на некотором участке конечной площади. Из-за деформаций линия действия силы реакции Нормальная к плоскости составляющая силы реакции – это сила нормальной реакции Моментом силы трения качения
где
Опытным путём было установлено, что сила трения качения
Соотношение (2) носит название закона Кулона. Параметр
Экспериментально коэффициент трения качения можно определить, например, с помощью наклонного маятника (метод наклонного маятника). Маятник, используемый в лабораторной работе, – это металлический шарик, подвешенный на нити длиной
Шарик оказывает на плоскость давление, и сила нормального давления (рис. 3) равна
где Если отклонить шарик от положения равновесия (при натянутой нити) на некоторый угол Механическая энергия маятника складывается из кинетической и потенциальной энергий. В тех точках, где мятник максимально отклонён от положения равновесия (эти точки называются точками поворота) его кинетическая энергия равна нуля, а потенциальная максимальна. При движении маятника от одной точки поворота до другой из-за трения качения потенциальная энергия маятника уменьшится. За
где
Подставляя (5) в (4) и учитывая (6), получим
Работу, совершаемую против сил трения, можно вычислить по формуле
где
Приравнивая правые части уравнений (7) и (9), получим
В данной лабораторной работе возможные углы | |||
|
| Поделиться: |


 Маятник Максвелла представляет собой массивный диск, насаженный на стержень, и подвешенный бифилярно с помощью нитей к горизонтальной опоре (рис.1).
Маятник Максвелла представляет собой массивный диск, насаженный на стержень, и подвешенный бифилярно с помощью нитей к горизонтальной опоре (рис.1).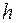 (рис. 1) относительно положения равновесия
(рис. 1) относительно положения равновесия 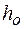 (крайнего нижнего положения) и отпустить, то, предоставленный самому себе, маятник начнет поступательное движение вниз, одновременно вращаясь вокруг оси симметрии. При этом запасённая маятником потенциальная энергия будет переходить в кинетическую энергию поступательного и вращательного движения.
(крайнего нижнего положения) и отпустить, то, предоставленный самому себе, маятник начнет поступательное движение вниз, одновременно вращаясь вокруг оси симметрии. При этом запасённая маятником потенциальная энергия будет переходить в кинетическую энергию поступательного и вращательного движения. Достигнув положения равновесия, маятник, у которого потенциальная энергия полностью перешла в кинетическую, не остановится. Он по инерции будет продолжать вращение, нити начнут наматываться на стержень (уже с другой стороны), и маятник вновь поднимется вверх. Однако из-за убыли механической энергии вследствие трения нитей о стержень и сопротивления воздуха расстояние, пройденное маятником при подъеме, окажется меньше, чем при спуске.
Достигнув положения равновесия, маятник, у которого потенциальная энергия полностью перешла в кинетическую, не остановится. Он по инерции будет продолжать вращение, нити начнут наматываться на стержень (уже с другой стороны), и маятник вновь поднимется вверх. Однако из-за убыли механической энергии вследствие трения нитей о стержень и сопротивления воздуха расстояние, пройденное маятником при подъеме, окажется меньше, чем при спуске.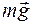 и
и 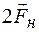 (
( - сила натяжения одной нити), и маятник движется с постоянным ускорением
- сила натяжения одной нити), и маятник движется с постоянным ускорением  .
. . (1)
. (1) потенциальная энергия маятника, поднятого на высоту
потенциальная энергия маятника, поднятого на высоту  кинетическая энергия поступательного и вращательного движения маятника в нижней точке траектории (
кинетическая энергия поступательного и вращательного движения маятника в нижней точке траектории (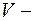 скорость поступательного движения центра масс маятника,
скорость поступательного движения центра масс маятника,  угловая скорость,
угловая скорость,  момент инерции маятника относительно оси симметрии).
момент инерции маятника относительно оси симметрии). , получаем:
, получаем: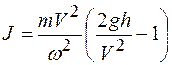 . (2)
. (2) ,
,  , (3)
, (3)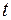 – время, за которое маятник опустился с высоты
– время, за которое маятник опустился с высоты  , (4)
, (4) радиус стержня.
радиус стержня. . (5)
. (5) , (6)
, (6) момент инерции стержня относительно оси вращения (
момент инерции стержня относительно оси вращения (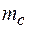 – масса стержня,
– масса стержня, 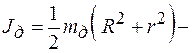 момент инерции диска относительно той же оси (
момент инерции диска относительно той же оси (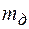 –масса диска,
–масса диска,  внешний радиус диска).
внешний радиус диска). (по нижнему краю диска). Одновременно отпустив маятник и включив секундомер, измерить время движения маятника
(по нижнему краю диска). Одновременно отпустив маятник и включив секундомер, измерить время движения маятника  ), пройденное маятником. Опыт проделать ещё два раза
), пройденное маятником. Опыт проделать ещё два раза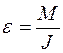 , (1)
, (1) угловое ускорение тела,
угловое ускорение тела,  результирующий момент относительно этой оси всех внешних сил, действующих на тело,
результирующий момент относительно этой оси всех внешних сил, действующих на тело, 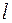 от оси вала насажены цилиндры Е. Вся система может свободно вращаться относительно неподвижной горизонтальной оси ОО', совпадающей с осью вала. Момент инерции системы можно менять, передвигая цилиндры по стержням или снимая их со стержней. На валу закрепляется нить
от оси вала насажены цилиндры Е. Вся система может свободно вращаться относительно неподвижной горизонтальной оси ОО', совпадающей с осью вала. Момент инерции системы можно менять, передвигая цилиндры по стержням или снимая их со стержней. На валу закрепляется нить  , к свободному концу которой привязывается груз
, к свободному концу которой привязывается груз  (чашка с разновесами).
(чашка с разновесами). .
. , приложенной к валу (силы трения в данной установке пренебрежимо малы). Момент этой силы относительно оси ОО' равен
, приложенной к валу (силы трения в данной установке пренебрежимо малы). Момент этой силы относительно оси ОО' равен , (2)
, (2)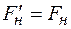 , где
, где  модуль силы натяжения нити, действующей на груз
модуль силы натяжения нити, действующей на груз  под действием силы тяжести
под действием силы тяжести  , откуда
, откуда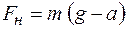 .
.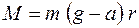 . (3)
. (3) , (4)
, (4) (
( диаметр вала, на который наматывается нить), получаем
диаметр вала, на который наматывается нить), получаем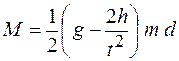 . (5)
. (5) точек на ободе вала соотношением
точек на ободе вала соотношением . (6)
. (6) , и из (4) и (6) следует
, и из (4) и (6) следует . (7)
. (7) . (8)
. (8)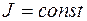 ), но его вращение происходит под действием различных по величине моментов сил
), но его вращение происходит под действием различных по величине моментов сил 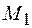 и
и  , то, в соответствии с (1),
, то, в соответствии с (1),  ,
, 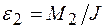 , и должно выполняться равенство
, и должно выполняться равенство . (9)
. (9)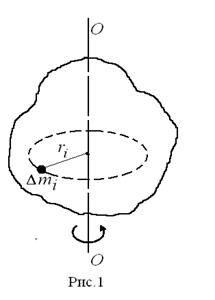 Моментом инерции твердого тела относительно оси ОО (рис.1) называется физическая величина
Моментом инерции твердого тела относительно оси ОО (рис.1) называется физическая величина 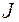 , равная сумме произведений всех элементарных масс
, равная сумме произведений всех элементарных масс 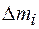 на квадрат их расстояний
на квадрат их расстояний  от оси:
от оси: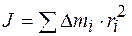 . (1)
. (1) , (2)
, (2) плотность вещества в элементе объема
плотность вещества в элементе объема  , находящегося на расстоянии
, находящегося на расстоянии  от оси вращения.
от оси вращения.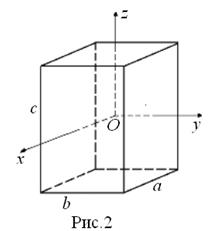 Момент инерции тела характеризует распределение его массы относительно оси вращения и является мерой инертности тела при вращательном движении. Момент инерции зависит от материала, формы и размеров тела, а также от положения оси.
Момент инерции тела характеризует распределение его массы относительно оси вращения и является мерой инертности тела при вращательном движении. Момент инерции зависит от материала, формы и размеров тела, а также от положения оси.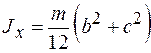 ,
, 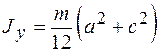 ,
, 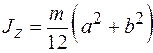 , (3)
, (3) масса параллелепипеда,
масса параллелепипеда,  стороны параллелепипеда, параллельные соответственно осям
стороны параллелепипеда, параллельные соответственно осям  ,
,  и
и 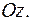
 Крутильные колебания – это колебания, которые совершает тело (система тел), подвешенное на упругой проволоке, под действием момента упругих сил, возникающих в проволоке при ее закручивании (рис.3). Известно, что период
Крутильные колебания – это колебания, которые совершает тело (система тел), подвешенное на упругой проволоке, под действием момента упругих сил, возникающих в проволоке при ее закручивании (рис.3). Известно, что период  крутильных колебаний не зависит от угла закручивания, а зависит от момента инерции тела, упругих свойств проволоки и выражается формулой
крутильных колебаний не зависит от угла закручивания, а зависит от момента инерции тела, упругих свойств проволоки и выражается формулой , (4)
, (4)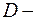 постоянная момента упругих сил.
постоянная момента упругих сил. , подвешенную вертикально с помощью двух натянутых вдоль одной прямой проволок. Рамка имеет крепежные винты, что позволяет устанавливать в ней различные тела, моменты инерции которых требуется определить.
, подвешенную вертикально с помощью двух натянутых вдоль одной прямой проволок. Рамка имеет крепежные винты, что позволяет устанавливать в ней различные тела, моменты инерции которых требуется определить.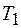 которых, согласно (4), определится выражением:
которых, согласно (4), определится выражением: , (5)
, (5) момент инерции рамки,
момент инерции рамки,  момент инерции исследуемого тела,
момент инерции исследуемого тела, 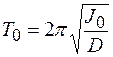 . (6)
. (6) выражение:
выражение: . (7)
. (7)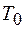 и рамки с закрепленным в ней исследуемым телом
и рамки с закрепленным в ней исследуемым телом 
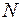 полных колебаний, а затем рассчитывают периоды по формулам:
полных колебаний, а затем рассчитывают периоды по формулам: и
и  , (8)
, (8) время
время  время
время 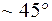 от положения равновесия и отпустить. Пропустив одно – два колебания, включить секундомер и измерить время
от положения равновесия и отпустить. Пропустив одно – два колебания, включить секундомер и измерить время  15─20 полных колебаний. Измерения
15─20 полных колебаний. Измерения 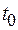 провести не менее трех раз при одном и том же числе колебаний
провести не менее трех раз при одном и том же числе колебаний 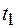 такого же числа полных колебаний системы (рамки с параллелепипедом). Результаты измерений занести в табл.1.
такого же числа полных колебаний системы (рамки с параллелепипедом). Результаты измерений занести в табл.1. (см. рис.2). Занести в табл.2 результаты измерений и массу
(см. рис.2). Занести в табл.2 результаты измерений и массу  ) происходит значительное изменение скоростей тел. Во многих случаях систему взаимодействующих при ударе тел можно считать замкнутой, т. к. силы взаимодействия (ударные силы) превосходят все внешние силы, действующие на тела.
) происходит значительное изменение скоростей тел. Во многих случаях систему взаимодействующих при ударе тел можно считать замкнутой, т. к. силы взаимодействия (ударные силы) превосходят все внешние силы, действующие на тела. , называемая коэффициентом восстановления скорости.
, называемая коэффициентом восстановления скорости. , (1)
, (1) относительная скорость тел до соударения,
относительная скорость тел до соударения, 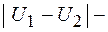 относительная скорость тел после соударения.
относительная скорость тел после соударения.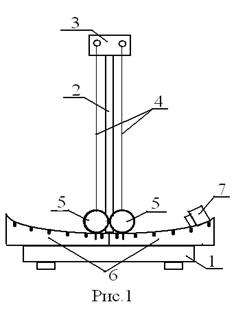 Коэффициент восстановления скорости зависит от упругих свойств материала соударяющихся тел. Для абсолютно упругого удара
Коэффициент восстановления скорости зависит от упругих свойств материала соударяющихся тел. Для абсолютно упругого удара 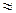 0.5, из стали
0.5, из стали  Установка для изучения соударения шаров схематически изображена на рис.1. Она состоит из основания 1 с регулируемыми опорами, на котором закреплена стойка 2 с двумя кронштейнами. На верхнем кронштейне 3 расположен механизм закрепления бифилярных нитей-подвесов 4 для шаров 5. На нижнем кронштейне закреплены измерительные шкалы 6, проградуированные в градусной мере. На правой шкале находится электромагнит 7, который может перемещаться вдоль шкалы и фиксироваться в определенном положении.
Установка для изучения соударения шаров схематически изображена на рис.1. Она состоит из основания 1 с регулируемыми опорами, на котором закреплена стойка 2 с двумя кронштейнами. На верхнем кронштейне 3 расположен механизм закрепления бифилярных нитей-подвесов 4 для шаров 5. На нижнем кронштейне закреплены измерительные шкалы 6, проградуированные в градусной мере. На правой шкале находится электромагнит 7, который может перемещаться вдоль шкалы и фиксироваться в определенном положении. он приобретет потенциальную энергию
он приобретет потенциальную энергию  (
(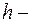 высота поднятия центра масс шара,
высота поднятия центра масс шара, 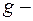 ускорение свободного падения). Если шар отпустить, то при возвращении шара к положению равновесия его потенциальная энергия полностью перейдет в кинетическую.
ускорение свободного падения). Если шар отпустить, то при возвращении шара к положению равновесия его потенциальная энергия полностью перейдет в кинетическую. , (2)
, (2) скорость шара 1 при достижении им положения равновесия (перед соударением с шаром 2). Из (2) следует:
скорость шара 1 при достижении им положения равновесия (перед соударением с шаром 2). Из (2) следует: . (3)
. (3) (угол отклонения) и
(угол отклонения) и 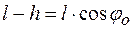 , т.е.
, т.е. 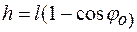 . Так как
. Так как  , то
, то . (4)
. (4) . Если угол
. Если угол  мал, то
мал, то  и, следовательно,
и, следовательно, =
= 
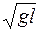 . (5)
. (5) и
и  ─ скоростей шаров после соударения:
─ скоростей шаров после соударения: ,
,  (6)
(6)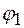 и
и 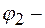 углы отклонения от вертикали нитей-подвесов шаров после удара.
углы отклонения от вертикали нитей-подвесов шаров после удара. =0, получим:
=0, получим: . (7)
. (7) ) шаров. Значения углов занести в таблицу.
) шаров. Значения углов занести в таблицу.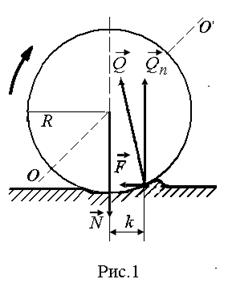 При качении по плоской поверхности тел, обладающих осевой симметрией (цилиндр или шар), возникает трение качения.
При качении по плоской поверхности тел, обладающих осевой симметрией (цилиндр или шар), возникает трение качения. плоской поверхности не совпадает с линией действия силы нормального давления
плоской поверхности не совпадает с линией действия силы нормального давления 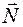 тела (рис.1), и возникает момент силы реакции относительно оси
тела (рис.1), и возникает момент силы реакции относительно оси 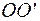 , который замедляет вращение тела.
, который замедляет вращение тела. , а касательная к плоскости составляющая – сила трения качения
, а касательная к плоскости составляющая – сила трения качения 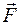 .
. называют момент силы нормальной реакции относительно оси вращения, т.е.
называют момент силы нормальной реакции относительно оси вращения, т.е. ,
, – плечо силы
– плечо силы  . При малых остаточных деформациях
. При малых остаточных деформациях  и можно считать, что
и можно считать, что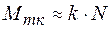 . (1)
. (1) пропорциональна моменту силы трения, записанному в виде (1), и обратно пропорциональна радиусу
пропорциональна моменту силы трения, записанному в виде (1), и обратно пропорциональна радиусу  катящегося тела:
катящегося тела: . (2)
. (2)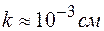 ), физического состояния соприкасающихся поверхностей, скорости катящегося тела и других факторов.
), физического состояния соприкасающихся поверхностей, скорости катящегося тела и других факторов. к основанию (рис. 2).
к основанию (рис. 2).

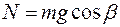 ,
, 
 (рис. 2) и отпустить, то шарик начнёт перекатываться по наклонной плоскости, причём его движение по плоскости будет иметь характер затухающих колебаний. Затухание обусловлено, в основном, трением качения (механическая энергия маятника уменьшается, т.к. совершается работа против сил трения).
(рис. 2) и отпустить, то шарик начнёт перекатываться по наклонной плоскости, причём его движение по плоскости будет иметь характер затухающих колебаний. Затухание обусловлено, в основном, трением качения (механическая энергия маятника уменьшается, т.к. совершается работа против сил трения). колебаний, когда максимальный угол отклонения уменьшился от
колебаний, когда максимальный угол отклонения уменьшился от  , потери потенциальной энергии маятника
, потери потенциальной энергии маятника  равны
равны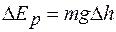 , (4)
, (4) – изменение высоты центра масс шарика. Из геометрических соотношений (рис. 2) следует:
– изменение высоты центра масс шарика. Из геометрических соотношений (рис. 2) следует: , (5)
, (5) . (6)
. (6)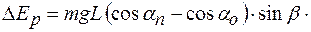 (7)
(7) , (8)
, (8) – путь, пройденный шариком за
– путь, пройденный шариком за  . Тогда, с учетом (2) и (3), формула (8) примет вид
. Тогда, с учетом (2) и (3), формула (8) примет вид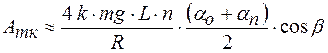 . (9)
. (9) .
. и
и 


