
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение расчетным путем прочности балки по нормальному сечениюСодержание книги
Поиск на нашем сайте
В основу расчета на прочность изгибаемых элементов по нормальным сечениям положена III стадия напряженно-деформированного состояния при изгибе. При относительно малых процентах армирования разрушение наступает, когда напряжения в растянутой арматуре достигают предельных значений Следует иметь в виду, что теоретический изгибающий момент, воспринимаемый сечением железобетонной балки непосредственно перед разрушением, вычисляется при фактических значениях сопротивления бетона Согласно п. 3.1.6.2 ДБН [1], при выполнении проверочных расчетов прямоугольных сечений можно предполагать равномерный характер распределения нормальных сжимающих напряжений в сжатой зоне (рис. 2 а). Коэффициент Для сечения прямоугольного профиля, симметричного относительно оси, совпадающей с плоскостью изгиба (рис.2), из условия равенства нулю суммы проекций всех нормальных усилий на продольную ось элемента запишем
откуда
Определяем граничное значение относительной высоты сжатой зоны бетона
Заменив в формуле (7) относительные деформации продольной арматуры
Проверяется условие:
Если условие (9) выполняется, то теоретический изгибающий момент, воспринимаемый сечением непосредственно перед разрушением
или относительно оси, нормальной к плоскости изгиба и проходящей через точку приложения равнодействующей усилий в растянутой арматуре As,
Если условие (9) не выполняется, то для изгибаемых элементовиз бетона класса С25/30 и ниже с арматурой класса А240С-А500С допускается несущую способность (переармированного сечения балки) определять по формуле:
Значение теоретической разрушающей нагрузки Fk (рис.3) определяем по формуле:
Рис.2. Схема распределения напряжений и деформаций в сечении балки
Рис. 3. Схема испытания балки
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 141; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.191.6 (0.008 с.) |

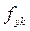 , а деформации крайнего сжатого волокна достигают предельных значений
, а деформации крайнего сжатого волокна достигают предельных значений  , что приводит к интенсивному раскрытию трещин, нормальных к продольной оси элемента, и их развитию по высоте сечения, уменьшению высоты сжатой зоны бетона и последующему ее разрушению при напряжениях в бетоне
, что приводит к интенсивному раскрытию трещин, нормальных к продольной оси элемента, и их развитию по высоте сечения, уменьшению высоты сжатой зоны бетона и последующему ее разрушению при напряжениях в бетоне 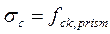 . Такое характерно для непереармированных сечений.
. Такое характерно для непереармированных сечений. и арматуры
и арматуры 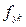 . При этом геометрические характеристики нормального сечения принимаются по данным непосредственных обмеров образца до и после испытания.
. При этом геометрические характеристики нормального сечения принимаются по данным непосредственных обмеров образца до и после испытания. определяет расчетную высоту сжатой зоны, коэффициент
определяет расчетную высоту сжатой зоны, коэффициент 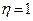 определяет воздействие различных факторов на прочность бетона.
определяет воздействие различных факторов на прочность бетона.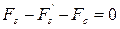 , (4)
, (4) (5)
(5) (6)
(6)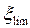 . По правилу подобия треугольников (рис. 2 а):
. По правилу подобия треугольников (рис. 2 а): , где
, где  (7)
(7) на
на  и высоту сжатой зоны бетона
и высоту сжатой зоны бетона 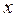 на относительную на
на относительную на  , получим
, получим (8)
(8)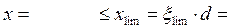 (9)
(9) , определяется по формуле:
, определяется по формуле: (10)
(10)
 (11)
(11)
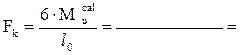 (12)
(12)




