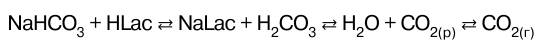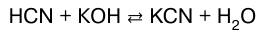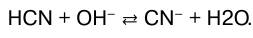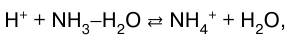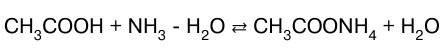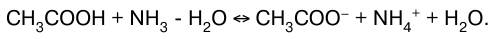Взаимосвязь между процессами обмена веществ и энергии в организме. Термодинамическая система

Оглавление

· 1. Взаимосвязь между процессами обмена веществ и энергии в организме. Термодинамическая система

· 2. Первое начало термодинамики. Понятия, характеризующие систему

· 3. Первое начало термодинамики

· 4. Закон Гесса

· 5. Второе начало термодинамики. Свободная энергия Гиббса

· 6. Второе начало термодинамики. Энтропия

· 7. Формула Больцмана

· 8. Энергия Гиббса

· 9. Растворы. Классификация растворов

· 10. Вода как растворитель

· 11. Концентрация раствора и способы ее выражения

· 12. Процесс растворения

· 13. Термодинамика процесса растворения

· 14. Растворимость

· 15. Растворимость газов в жидкостях. Законы Генри—Дальтона и Сеченова

· 16. Роль диффузии в процессах переноса веществ в биологических системах

· 17. Понижение температуры замерзания и повышение температуры кипения растворов

· 18. Осмотическое давление

· 19. Роль осмоса и осмотического давления в биологических системах

· 20. Степень диссоциации (ионизации). Сила электролитов

· 21. Константа диссоциации. Закон разведения Оствальда. Теория растворов сильных электролитов

· 22. Теория кислот и оснований

· 23. Буферные системы крови.Плазма крови

· 24. Реакции нейтрализации

· 25. Гидролиз соли

· 26. Реакция осаждения и растворения

· 27. Окислительно-восстановительные реакции

· 28. Окислители и восстановители

· 29. Биологическое значение окислительно-восстановительных процессов

· 30. Химическая связь и ее экспериментальные характеристики

· 31. Водородная связь.

· 32. Макро– и микроэлементы в среде и в организме человека

· 33. Топография важнейших биогенных элементов в организме человека

· 34. Биологическая роль химических элементов в организме

· 35. S-элементы и их соединения

· 36. Биологическая роль s-элементов IА-группы (литий, рубидий, цезий, франций)

· 37. Биологическая роль s-элементов IА-группы (натрий, калий)

· 38. Биологическая роль s-элементов IIА-группы. Их применение в медицине (бериллий, магний, кальций)

· 39. Биологическая роль d-элементов VIB-группы. Их применение в медицине

· 40. Биологическая роль соединений марганца. Их применение в медицине

· 41. Биологическая роль соединений железа. Гемоглобин

· 42. Биологическая роль соединений железа. Моноксид углерода СО.

· 43. Биологическая роль соединений железа и кобальта

· 44. Роль d-элементов IB-группы. Применение их соединений в медицине

· 45. Биологическая роль d-элементов IIB-группы. Применение их соединений в медицине

· 46. Токсические свойства соединений группы IIB (Zn, Cd, Hg)

· 47. Биологическая роль р-элементов IIIA-группы. Применение их соединений в медицине

· 48. Биологическая роль р-элементов IVA-группы. Применение их соединений в медицине

· 49. Биологическая роль р-элементов VA-группы. Применение их соединений в медицине (азот, фосфор)

· 50. Биологическая роль р-элементов VA-группы (мышьяк, сурьма, висмут). Применение их в медицине

· 51. Биологическая роль р-элементов VIA-группы. Применение их соединений в медицине

· 52. Биологическая роль р-элементов VIIA-группы. Применение их соединений в медицине (фтор и хлор)

· 53. Биологическая роль р-элементов VIIA-группы. Применение их соединений в медицине (бром, йод)

· 54. Аэрозоли

· 55. Эмульсии

· 56. Коллоидные ПАВ

Первое начало термодинамики

Первое начало термодинамики относится к числу фун–даментальных законов природы, которые не могут быть выведены из каких-то других законов. Его справедливость доказывают многочисленные эксперименты, в частности неудачные попытки построить вечный двигатель первого рода, т. е. такую машину, которая смогла бы как угодно долго совершать работу без подвода энергии извне.

В зависимости от условий протекания процесса в сис–теме используют различные функции состояния, которые выводят из первого начала термодинамики. При этом вместо сложных биологических систем для получения выводов о превращениях массы и энергии используют упрощенные модели. Давление в системе при этом под–держивается постоянным, оно равно внешнему давле–нию. Такие процессы, протекающие при р = const, назы–ваются изобарными. Работа расширения, совершае-мая при изобарном процессе, как известно, равна:

W = –ρΔV,

где ΔV – приращение объема системы, равное раз–ности объемов в состояниях 2 и 1.

Подставляя работу расширения в математическое выражение первого начала и проведя несложные пре–образования, получаем:

Q _ρ = ΔE + pΔV = (E₂ + ρV₂) – (E₁ + ρΔV₁)

где Qρ – теплота изобарного процесса;

1, 2 – индексы, относящиеся к началу и концу процесса.

Величина (E+ pV) – функция состояния системы, обоз–начаемая через Н и называемая энтальпией:

H = E + ρV.

Соответственно, выражение можно записать в виде:

Q _p = Н₂ – Н₁ = ΔH.

Из данного выражения следует, что энтальпия – функция состояния, приращение которой равно теп–лоте, полученной системой в изобарном процессе.

Измерение приращения энтальпии в некотором про–цессе может быть осуществлено при проведении это–го процесса в калориметре при постоянном давлении. Именно так проводили свои эксперименты А. М. Ла–вуазье и П. С. Лаплас, изучая энергетику метаболиз–ма в живом организме.

В тех случаях, когда изменение состояния системы происходит при постоянном объеме, процесс называ–ется изохорным. Изменение объема AV при этом рав–но нулю, и в соответствии с формулой работа расшире–ния W = 0. Тогда из математического выражения первого начала термодинамики следует:

Q _v = ΔE.

Из вышеуказанного соотношения вытекает термо–динамическое определение: внутренняя энергия – функция состояния, приращение которой равно теп–лоте Q V, полученной системой в изохорном процессе. Следовательно, изменение внутренней энергии в не–котором процессе может быть измерено при проведе–нии этого процесса в калориметре при постоянном объеме. Следует, что при ρ = const приращения внут–ренней энергии и энтальпии связаны соотношением:

ΔH = ΔE + ρΔV.

Закон Гесса

Раздел термодинамики, изучающий превращения энер–гии при химических реакциях, называется химической термодинамикой. Уравнение реакции, для которой ука–зываются соответствующие этой реакции изменения внут–ренней энергии ΔE, энтальпии ΔH или какой-либо другой функции состояния, называется термохимическим.

Химические реакции, при протекании которых проис–ходит уменьшение энтальпии системы (ΔH < 0) и во внеш–нюю среду выделяется теплота, называются экзотерми–ческими.

Реакции, в результате которых энтальпия возрастает (ΔH > 0) и система поглощает теплоту Q _p извне, назы–ваются эндотермическими.

Окисление глюкозы кислородом происходит с выде–лением большого количества теплоты (Q_p = –2800 кДж/ /моль), т. е. этот процесс – экзотермический. Соответ–ствующее термохимическое уравнение запишется в виде

С₆ Н₁₂ О₆ + 60₂ = 6С0₂ + 6Н₂О, ΔH = –2800 кДж.

Реакции, протекающие в растворе, сопровождаются обычно незначительным изменением объема системы, т. е. ΔV ≈ 0. В связи с этим во многих случаях при биоло–гических расчетах можно считать, что ΔH = ΔE. Следова–тельно, выделение теплоты в таких системах обусловлено в основном уменьшением внутренней энергии в результа–те протекания реакции, и наоборот.

Энтальпией образования соединения А называется изменение энтальпии системы ΔH_A, сопровождающее образование 1 моля соединения А из простых веществ.

Энтальпии образования кислорода, углерода, водо–рода и всех других элементных (простых) веществ при–нимают равными нулю.

При прочих равных условиях внутренняя энер–гия и энтальпия пропорциональны количеству ве–щества в системе. Такие термодинамические функции называются экстенсивными.

С точки зрения термодинамики реакция общего ви–да n_AА + п_В = п_С + n_D, Δh представляет собой пере–ход системы из начального состояния с энтальпией Н₁ в состояние 2 с энтальпией Н₂. Изменение энтальпии системы в результате этого перехода, называемое энтальпией данной реакции, равно разности:

ΔH_p-я = Н₂ – Н₁ = (n _c H _c + n_DH_D) – (n_АН_А + n_BH_B).

Закон постоянства тепловых сумм, открыт русским ученым-химиком Г. И. Гессом в 1840 г. Он является пер–вооткрывателем применимости первого начала термо–динамики при химических превращениях и основателем химической термодинамики. В настоящее время закон Гесса рассматривается как следствие первого начала термодинамики и формулируется так: приращение энтальпии при образовании заданных продуктов из данных реагентов при постоянном давлении не за–висит от числа и вида реакций, в результате кото–рых образуются эти продукты.

При термохимических расчетах чаще применяется не сам закон Гесса, а его следствие, выведенное выше для частного случая окисления глюкозы в виде равен–ства (2). Для реакции, представленной в общем виде п_АА + п_вВ = = п_сС + n_DD, следствие из закона Гесса записы–вается с помощью равенства ΔH_p-я = (n_CΔH_C + n_DΔH_D) – (n_AΔH_A + + n_BΔH_B) и формулируется так: энтальпия реакции равна алгебраической сумме энтальпий об–разования стехиометрического количества продук–тов за вычетом алгебраической суммы энтальпий образования стехиометрического количества реагентов.

Формула Больцмана

Изолированные системы по определению не обме–ниваются с внешней средой ни веществом, ни энер–гией. Конечно, реально таких систем в природе не су–ществует. Однако очень хорошая изоляция может быть осуществлена, если поместить систему в термос, за–крытый пробкой.

Оказывается, что любой самопроизвольный процесс может протекать в изолированной системе лишь в том случае, когда он характеризуется увеличением энтро–пии; в равновесии энтропия системы постоянна:

ΔS ≥ 0.

Это утверждение, основанное на эксперименталь–ных наблюдениях, является одной из возможных фор–мулировок второго начала термодинамики.

Процесс, обратный самопроизвольному, согласно второму началу термодинамики в изолированной систе–ме протекать не может, так как такой процесс характе–ризуется уменьшением энтропии.

Рассмотрение различных изолированных систем по–казывает, что самопроизвольные процессы всегда связаны с ростом числа микросостояний w системы. В этих же процессах происходит возрастание энтропии S системы, т. е. энтропия возрастает с увеличением числа микросостояний. Впервые на существование та–кой зависимости обратил внимание австрийский фи–зик Л. Больцман, который в 1872 г. предложил соотно–шение:

К_Б = R / N_A = 1,38 – 10^-23 Дж/К,

где К_Б – постоянная Больцмана, равная отношению газовой постоянной R к постоянной Авогадро N_A.

Это соотношение называется формулой Больц-мана.

Формула Больцмана позволяет теоретически рас–считать энтропию системы по числу возможных ее микросостояний. Такие расчеты хорошо согласуются с экспериментально определенными значениями. В частности, известно, что число микросостояний кристаллических веществ при 0°К близко к w ₀ «1. Та–ким образом, могут быть определены абсолютные зна–чения энтропии кристаллизующихся веществ в отличие от внутренней энергии Е и энтальпии Н, для которых можно определить лишь относительные значения.

Увеличение числа микросостояний системы во мно–гих случаях можно связать с ростом неупорядоченно–сти в этой системе, с переходом к более вероятным распределениям энергии системы. Исходя из соотно–шения Больцмана, можно дать молекулярно-кинетиче-ское определение энтропии.

Энтропия есть мера вероятности пребывания системы в данном состоянии или мера неупоря–доченности системы.

Важное значение понятия энтропии связано с тем, что на основе этой величины можно прогнозировать направление самопроизвольного протекания процес–сов. Однако применимость измерения энтропии как критерия направленности процессов ограничивается изолированными системами в соответствии с форму–лировкой второго начала термодинамики.

Энергия Гиббса

В качестве критерия самопроизвольности процес–сов в открытых и закрытых системах вводится новая функция состояния – энергия Гиббса. Эта функция получила название в честь великого американского физика Д. У. Гиббса (1839—1903), который вывел эту функцию, а затем использовал в термодинамических работах.

Энергия Гиббса определяется через энтальпию Н и энтропию S с помощью соотношений:

G = H – S,

ΔG = ΔH – ΔS.

На основе энергии Гиббса второе начало термодина–мики можно сформулировать следующим образом: в изобарно-изотермических условиях (р, Т = const) в системе самопроизвольно могут осуществляться только такие процессы, в результате которых энер–гия Гиббса системы уменьшается (ΔG <0).В со–стоянии равновесия энергия Гиббса системы не ме–няется (G = const, AG = 0).

ΔG < 0, р, Т = const.

Из изложенного вытекает, что энергия Гиббса игра–ет большую роль в изучении биоэнергетических про–цессов. С помощью этой функции состояния можно прогнозировать направление самопроизвольных про–цессов в биологических системах и рассчитывать мак-сималь-но достижимый КПД.

Энергия Гиббса G так же, как и энтальпия Н, являет–ся функцией состояния системы. Поэтому изменение энергии Гиббса ΔG может использоваться для харак–теристики химических превращений аналогично изме–нению энтальпии ΔН. Уравнения реакции, для которых указывается соответствующее этим реакциям изменение энергии Гиббса, также называются термо–химическими.

Химические реакции, при протекании которых про–исходит уменьшение энергии Гиббса системы (ΔG < 0) и совершается работа, называются экзергоническими. Реакции, в результате которых энергия Гиббса возрас–тает (ΔG > 0) и над системой совершается работа, называются эндергоническими.

Выведенная на основе второго начала термодина–мики энергия Гиббса является функцией состояния. Следовательно, так же, как и для энтальпии, может быть сформулирован закон Гесса для энергии Гиббса в следующей форме: изменение энергии Гиббса при образовании заданных продуктов из данных реа–гентов при постоянных давлении и температуре не зависит от числа и вида реакций, в результате ко–торых образуются эти продукты.

Важный пример применения закона Гесса – расчет энергии Гиббса реакции окисления глюкозы дикисло-родом. Изменение энергии Гиббса в этой реакции при р = 101 кПа и Т = 298°К, определенное вне организма, равно ΔG° = –2880 кДж/моль. Соответствующее тер–мохимическое уравнение записывается в виде:

С₆Н₁₂О₆ + 6О₂ = 6СО₂ + 6Н₂О, ΔG_p-я° = –2880 кДж/моль.

В клетках организма эта реакция осуществляется через целый ряд последовательных стадий, изучен–ных биохимиками. Можно предсказать исходя из за–кона Гесса, что сумма изменений энергии Гиббса во всех промежуточных реакциях равна ΔG_p-я:

ΔG₁ + ΔG₂ + ΔG₃ + … + ΔG_n = ΔG_p-я °.

Энергия Гиббса реакции равна алгебраической сумме энергий Гиббса образования стехиометри-ческого количества продуктов за вычетом алге–браической суммы энергий Гиббса образования стехиометрического количества реагентов:

ΔG_p-я = (n_cΔG_c + n_DΔG_D)-(n_AΔG_A + n_BΔG_B).

Вода как растворитель

Самым распространенным растворителем на нашей планете является вода. Тело среднего человека мас–сой 70 кг содержит примерно 40 кг воды. При этом около 25 кг воды приходится на жидкость внутри клеток, а 15 кг составляет внеклеточная жидкость, в которую входят плазма крови, межклеточная жидкость, спинно-моз-говая жидкость, внутриглазная жидкость и жидкое содержимое желудочно-кишечного тракта. У животных и растительных организмов вода составляет обычно бо–лее 50%, а в ряде случаев содержание воды достигает 90—95%.

Вследствие своих аномальных свойств вода – уни–кальный растворитель, прекрасно приспособленный для жизнедеятельности.

Прежде всего вода хорошо растворяет ионные и мно–гие полярные соединения. Такое свойство воды связа–но в значительной мере с ее высокой диэлектрической проницаемостью (78,5).

Другой многочисленный класс веществ, хорошо раст–воримых в воде, включает такие полярные органиче–ские соединения, как сахара, альдегиды, кетоны, спир–ты. Их растворимость в воде объясняется склонностью молекул воды к образованию полярных связей с поляр–ными функциональными группами этих веществ, на–пример с гидроксильными группами спиртов и сахаров или с атомом кислорода карбонильной группы альдеги–дов и кетонов. Ниже приведены примеры водородных связей, важных для растворимости веществ в биологи–ческих системах. Вследствие высокой полярности во–да вызывает гидролиз веществ.

Так как вода составляет основную часть внутренней среды организма, то она обеспечивает процессы всасывания, передвижения питательных веществ и продуктов обмена в организме.

Необходимо отметить, что вода является конечным продуктом биологического окисления веществ, в частно–сти глюкозы. Образование воды в результате этих про–цессов сопровождается выделением большого коли–чества энергии – приблизительно 29 кДж/моль.

Важны и другие аномальные свойства воды: высо–кое поверхностное натяжение, низкая вязкость, высо–кие температуры плавления и кипения и более высокая плотность в жидком состоянии, чем в твердом.

Для воды характерно наличие ассоциатов – групп молекул, соединенных водородными связями.

В зависимости от сродства к воде функциональные группы растворяемых частиц подразделяются на гид–рофильные (притягивающие воду), легко сольватируе-мые водой, гидрофобные (отталкивающие воду) и ди-фильные.

К гидрофильным группам относятся полярные функ–циональные группы: гидроксильная —ОН, амино —NH₂, тиольная —SH, карбоксильная —СООН. К гидрофоб–ным – неполярные группы, например углеводородные радикалы: СНз—(СН₂)_п —, С₆Н₅ —. К дифильным отно–сят вещества (аминокислоты, белки), молекулы кото–рых содержат как гидрофильные группы (—ОН, —NH₂, —SH, —СООН), так и гидрофобные группы: (СН₃ – (СН₂)_п, — С₆Н₅—).

При растворении дифильных веществ происходит изменение структуры воды как результат взаимодей–ствия с гидрофобными группами. Степень упорядо–чения молекул воды, близко расположенных к гидро–фобным группам, увеличивается, и контакт молекул воды с гидрофобными группами сводится к миниму–му. Гидрофобные группы, ассоциируясь, выталки–вают молекулы воды из области своего расположения.

Процесс растворения

Природа процесса растворения сложна. Естественно, возникает вопрос, почему некоторые вещества легко рас–творяются в одних растворителях и плохо растворимы или практически нерастворимы в других.

Образование растворов всегда связано с теми или иными физическими процессами. Одним из таких про–цессов является диффузия растворенного вещества и растворителя. Благодаря диффузии частицы (молеку–лы, ионы) удаляются с поверхности растворяющегося вещества и равномерно распределяются по всему объему растворителя. Именно поэтому в отсутствие пе–ремешивания скорость растворения зависит от скорос–ти диффузии. Однако нельзя лишь физическими процес–сами объяснить неодинаковую растворимость веществ в различных растворителях.

Великий русский химик Д. И. Менделеев (1834—1907) считал, что важную роль при растворении играют хими–ческие процессы. Он доказал существование гидратов серной кислоты

H₂SО₄H₂O, H₂SО₄2H₂O, H₂SО₄4H₂О и некоторых других веществ, например, С₂Н₅ОН3Н₂О. В этих случаях растворение сопровождается образовани–ем химических связей частиц растворяемого вещества и растворителя. Этот процесс называется сольватаци–ей, в частном случае, когда растворителем является во–да, – гидратацией.

Как установлено, в зависимости от природы раство–ренного вещества сольваты (гидраты) могут образо–вываться в результате физических взаимодействий: ион-дипольного взаимодействия (например, при рас–творении веществ с ионной структурой (NaCI и др.); диполь-дипольного взаимодействия – при растворе–нии веществ с молекулярной структурой (органичес–кие вещества)).

Химические взаимодействия осуществляются за счет донорно-акцепторных связей. Здесь ионы раст–воренного вещества являются акцепторами электронов, а растворители (Н₂О, NН₃) – донорами электро–нов (например, образование аквакомплексов), а также в результате образования водородных связей (например, растворение спирта в воде).

Доказательствами химического взаимодействия раст–воренного вещества с растворителем являются теп–ловые эффекты и изменение окраски, сопровождаю–щие растворение.

Например, при растворении гидроксида калия в во–де выделяется теплота:

КОН + хН₂О = КОН(Н₂О)х; ΔН°_раств = –55 кДж/моль.

А при растворении хлорида натрия теплота погло–щается:

NaCI + хН₂О = NaCI(H₂О)х; ΔН°_раств = +3,8 кДж/моль.

Теплота, выделяемая или поглощаемая при раство–рении 1 моля вещества, называется теплотой раст–ворения Q_раств

В соответствии с первым началом термодинамики

Q_раств = ΔН_раств,

где ΔН_раств – изменение энтальпии при растворе–нии данного количества вещества.

Растворение в воде безводного сульфата меди бело–го цвета приводит к появлению интенсивной голубой окраски. Образование сольватов, изменение окраски, тепловые эффекты, как и ряд других факторов, свиде–тельствуют об изменении химической природы компо–нентов раствора при его образовании.

Таким образом, в соответствии с современными представлениями, растворение – физико-химический процесс, в котором играют роль как физические, так и химические виды взаимодействия.

Растворимость

Если растворимое вещество контактирует с раство–рителем, процесс образования раствора во многих слу–чаях идет самопроизвольно до тех пор, пока не достига–ется некоторая предельная концентрация (наступает насыщение). Это происходит при достижении равнове–сия, когда энтальпийный и энтропийный факторы срав–няются, т. е. ΔН = TΔS.

Например, при внесении кристаллов в жидкость с по–верхности кристалла в раствор переходят молекулы или ионы. Вследствие диффузии частицы равномерно рас–пределяются по всему объему растворителя. Растворе–ние идет до насыщения.

Раствор, содержащий при данной температуре мак–симальное количество растворенного вещества и нахо–дящийся в равновесии с избытком растворяемого ве–щества, называется насыщенным.

Перенасыщенный раствор – раствор, концентра–ция которого выше, чем в насыщенном.

Раствор с меньшей концентрацией, чем насыщен–ный, называют ненасыщенным.

Способность вещества растворяться в том или ином растворителе называется растворимостью. Численно растворимость вещества равна концентрации его на–сыщенного раствора.

Растворимость может быть выражена в тех же едини–цах, что и концентрация, например через количество рас–творенного вещества, содержащегося в 1 л насыщен–ного раствора, моль/л, или через массу растворенного вещества в 100 г насыщенного раствора. Единицей раство–римости является грамм на 100 г растворителя. Соответ–ствующая величина называется коэффициентом раствори–мости.

Растворимость зависит от природы растворяемого вещества и растворителя, температуры, давления, при–сутствия в растворе других веществ.

14б Влияние на растворимость природы компо–нентов

Способность веществ растворяться определяется характером сил взаимодействия между молекулами компонентов раствора X₁ и Х₂: растворитель – раство–ритель (X₁ – X₁), растворенное вещество – растворен–ное вещество (Х₂ – Х₂), растворитель – растворенное вещество (Х₁ – Х₂) (точки обозначают молекулярную связь).

Растворимость веществ колеблется в широких пре–делах. В примерах приведена растворимость различных солей в одном и том же растворителе (воде) и раство–римость одного и того же вещества (AgNО₃) в различных растворителях.

Вещества с ионным типом связи и вещества, состоя–щие из полярных молекул, лучше растворяются в поляр–ных растворителях, таких как вода, спирты. Эти раство–рители характеризуются высокой диэлектрической проницаемостью.

Высокая растворимость веществ довольно часто обус–ловлена образованием межмолекулярных, в частности водородных, связей. Так, неограниченная взаимная раст–воримость воды и спирта объясняется образованием водородных связей между молекулами воды и спирта, а растворение кристаллов AgcI в водном растворе ам–миака объясняется образованием химической донор-но-акцепторной связи иона серебра с молекулами ам–миака (AgCI в воде практически нерастворим). По этой же причине в пиридине – растворителе с низкой диэлек–трической проницаемостью – обнаруживается очень высокая растворимость.

Так как растворимость характеризует истинное рав–новесие, влияние внешних условий на это состояние (давления, температуры) можно качественно оценить, воспользовавшись принципом Ле Шателье. Подобные оценки необходимы в практике глубоководных погруже–ний, при работе в горячих цехах и т. п.

Осмотическое давление

Осмосом называется преимущественно односторон–нее проникновение молекул растворителя (диффузия) через полупроницаемую мембрану из растворителя в раствор или из раствора с меньшей концентрацией в раствор с большей концентрацией.

Необходимым условием возникновения осмоса яв–ляется наличие растворителя и раствора или двух раст–воров различной концентрации, разделенных полупро–ницаемой мембраной.

С точки зрения термодинамики движущей силой осмо–са является стремление системы к выравниванию кон–центраций, так как при этом энтропия системы возраста–ет, поскольку система переходит в менее упорядоченное состояние, энергия Гиббса системы соответственно уменьшается, химические потенциалы выравниваются. Поэтому осмос – самопроизвольный процесс.

Иллюстрацией, поясняющей связь механизма осмо–са с изменением давления пара над раствором, может служить простой опыт. Если в закрытый стеклянный со–суд поместить стакан с чистым растворителем и стакан с раствором какого-либо нелетучего вещества (уровни жидкостей в сосудах одинаковы), то через некоторое время уровень жидкости в первом стакане понизится, а уровень раствора во втором стакане повысится. В этом случае происходит переход растворителя из первого стакана во второй стакан, что обусловлено (по закону Рауля) более низким давлением пара рас–творителя над раствором, чем над чистым раствори–телем.

Таким образом, воздушное пространство между рас–творителем и раствором выполняет роль полупрони–цаемой мембраны.

Наполним сосуд с полупроницаемыми стенками вод–ным раствором глюкозы и поместим в другой сосуд с во–дой так, чтобы уровни жидкостей в этих сосудах совпа–дали. В результате осмоса объем раствора в первом сосуде увеличивается и уровень жидкости в этом сосуде постепенно повышается. При этом созда–ется препятствующее осмосу дополнительное гидро–статическое давление.

Гидростатическое давление столба жидкости при ос–мотическом равновесии определяет осмотическое дав–ление раствора.

Осмотическим давлением называется величина, измеряемая минимальным гидравлическим давле–нием, которое нужно приложить к раствору, чтобы осмос прекратился.

Законы осмотического давления.

Вант-Гофф предложил эмпирическое уравнение для расчета осмотического давления разбавленных раст–воров неэлектролитов:

π = С_(Х)RT,

где π – осмотическое давление, кПа;

С_(Х) – молярная концентрация, моль/л;

R – универсальная газовая постоянная, равная

8,31 кПа – л/(моль – К);

Т – абсолютная температура, К.

Хотя закон Вант—Гоффа был установлен на основе экспериментальных данных, он может быть выведен из условий термодинамического равновесия при ΔG = 0. Поэтому этот закон следует рассматривать как следст–вие второго начала термодинамики.

Выражение в вышеуказанной форме аналогично уравнению Клапейрона—Менделеева для идеальных газов, однако эти уравнения описывают разные про–цессы.

Теория кислот и оснований

Многие электролиты, в частности гидроксиды раз–личных элементов Э, проявляют свойства кислот или оснований. Диссоциация гидроксида ЭОН может про–текать по двум типам:

 

Разрыв может происходить по обеим связям группы

Э—О—Н.

Как известно, полярность и прочность связей зави–сят от разности электроотрицательностей элементов, размера и эффективного заряда атомов. Если энер–гия разрыва связи О—Н значительно меньше энергии разрыва связи Э—О, то диссоциация гидроксида про–текает по кислотному типу. Если же, наоборот, энер–гия разрыва связи О—Н значительно больше энергии разрыва связи Э—О, то диссоциация протекает по ос–новному типу.

В гидроксидах щелочных и щелочно-земельных ме–таллов, а также переходных металлов в низких степенях окисления прочность связи Э—О относительно мала, кислород более прочно связан с водородом, и диссо–циация Э—О—Н идет преимущественно по основному типу, т. е. с отщеплением гидроксидиона. Это связано с тем, что ионы таких элементов имеют довольно боль–шие размеры и малый эффективный заряд, т. е. они об–ладают слабой поляризующей способностью.

С возрастанием степени окисления увеличивается поляризующее действие атома Э (увеличение удельно–го заряда), кислород более прочно связан с элементом Э, и диссоциация Э—О—Н протекает преимуществен–но по кислотному типу, т. е. отщепляется водород-ион. Последнее связано с перераспределением электрон–22б ной плотности у атома кислорода. В результате связь Э—О становится прочнее, а связь О—Н – слабее.

В настоящее время не существует однозначного опре–деления понятий кислоты и основания, которое в равной мере можно было бы использовать для характеристики кислотно-основных взаимодействий в любых раствори–телях.

Для характеристики многих электролитов в водных растворах и в настоящее время можно использовать понятия кислоты, основания, данные Аррениусом:

1) кислотой называется электролит, диссоциирую–щий в растворах с образованием водород-ионов Н;

2) основанием называется электролит, диссоциирующий в растворах с образованием гидроксид-ионов ОН -;

3) амфолитом (амфотерным гидроксидом) называется электролит, диссоциирующий в растворе с образо–ванием как водород-ионов, так и гидроксид-ионов.

К амфолитам относят гидроксиды цинка, алюминия, хрома и других амфотерных элементов, а также ами–нокислоты, белки, нуклеиновые кислоты.

Применение принципа Ле Шателье к цепочке кислот–но-основных равновесий показывает, что с увеличе–нием в системе концентрации гидроксид-ионов ОН - воз–растает вероятность диссоциации по кислотному типу. Увеличение в системе концентрации водород-ионов Н+ приводит к преимущественной диссоциации по основ–ному типу. Это означает, что в кислой среде амфолит проявляет основной, а в щелочной среде – кислотный характер.

Например, гидроксид цинка при взаимодействии с кислотами ведет себя как основание:

Zn(OH)₂ + 2HCI – ZnCI ₂ + 2Н₂О,

а при взаимодействии с щелочами – как кислота:

Zn(ОН)₂+ 2NaOH → Na₂[Zn (OH)₄].

Плазма крови

Водород-карбонатная буферная система НСО₃ –/ Н₂СО₃ состоит из угольной кислоты Н₂СО₃ и сопряжен–ного основания НСО₃ –. Это наиболее важная буфер–ная система крови. Одим из компонентов – угольная кислота Н₂СО₃ – образуется при взаимодействии раст–воренного в плазме СО₂ с водой:

СО_2(р) + Н₂О н Н₂СО₃.

где СО_2(р) – концентрация растворенного СО₂.

Константа равновесия этой реакции:

К = [Н₂СО₃] / [СО₂]

Между СО₂ в альвеолах и водород-карбонатным буфером в плазме крови, протекающей через ка–пилляры легких, устанавливается цепочка равновесий.

Водород-карбонатная буферная система действует как эффективный физиологический буферный раствор вблизи рН7,4.

При поступлении в кровь кислот – доноров Н ⁺ равно–весие в цепочке по принципу Ле Шателье смещается влево в результате того, что ионы НСО₃ связывают ионы Н в молекулы Н₂СО₃. При этом концентрация Н₂СО₃ по–вышается, а концентрация ионов НСО₃ понижается. По–вышение концентрации Н₂СО₃ приводит к смещению равновесия влево, (принцип Ле Шателье). Это вызывает распад Н₂СО₃ и увеличение концентрации СО₂, раство–ренного в плазме. В результате смещается равновесие влево и повышается давление СО₂ в легких. Избыток СО₂ выводится из организма.

В результате водород-карбонатная система крови быстро приходит в равновесие с СO₂ в альвеолах и эф–фективно обеспечивает поддержание постоянства рН плазмы крови.

 

Таким образом, поддерживается нормальное зна–чение рН крови при слабо выраженном сдвиге рН, об–условленном ацидозом.

В замкнутых помещениях часто испытывают удушье (нехватку кислорода), учащение дыхания. Однако удушье связано не столько с недостатком кислорода, сколько с избытком СО 2.

Избыток СO₂ в атмосфере согласно закону Генри при–водит к дополнительному растворению СO₂ в крови. А это приводит к понижению рН крови, т. е. к ацидозу.

Водород-карбонатная буферная система наиболее быстро отзывается на изменение рН крови. Ее буферная емкость по кислоте составляет В_к = 40 ммоль/л плазмы крови, а буферная емкость по щелочи значительно мень–ше и равна примерно В_щ = 1—2 ммоль/л плазмы крови.

Реакции нейтрализации

Реакциями нейтрализации называются обменные реакции взаимодействия кислот и оснований, в резуль–тате которых образуются соль и вода.

Рассмотрим различные типы реакций нейтрализации.

1. Нейтрализация сильного основания сильной кис–лотой:

КОН + HNO₃ – KNO₃ + Н₂ O.

Молекулярно-ионное уравнение такой реакции Н⁺ + OН^- → Н₂O

и отрицательное значение энергии Гиббса ΔG° пока–зывают, что равновесие практически смещено в сто–рону образования воды.

Общим случаем реакции нейтрализации является взаимодействие кислот и оснований, различающихся по силе (степени диссоциации). Эти реакции не дохо–дят до конца вследствие протекания обратной реакции гидролиза соли.

2. Нейтрализация слабой кислоты сильным основа–нием:

 

или в молекулярно-ионном виде:

 

В данном случае реакция нейтрализации обратима. Обратима и реакция нейтрализации слабого основа–ния сильной кислотой:

 

или в молекулярно-ионном виде:

 

а также – слабого основания слабой кисло–той:

 

или в молекулярно-ионном виде:

 

В данных системах равновесие сильно смещено вправо, так как вода значительно более слабый элек–тролит, чем синильная кислота, аммиак и уксусная