
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пересечение объемов, или частичное совпадение объемов.
Например, в отношении «студент» и «отличник». Зона пересечения - это множество тех элементов, которые одновременно принадлежат обоим множествам. Пересечение имеет место в том случае, когда объем одного из понятий частично входит, а частично не входит в объем другого понятия. Пересекаться могут только общие понятия, например, «женщина» и «инженер», «лошадь» и «домашнее животное», «белый предмет» и «рояль» и др. Во всех этих парах понятия совместимы частично: часть женщин является инженерами, но часть женщин имеют другую профессию, часть инженеров - женщины, но есть и инженеры - мужчины и т.д. 5. Противоречие -отношение между понятиями,которые будучи несовместимыми исчерпывают суммой своих объемовобъем более общего, родового по отношению к ним понятия. В отношении противоречия будут находиться два понятия, в одном изкоторых отрицаются признаки предмета, зафиксированные в другомпонятии то есть: (В = не-А). Например: «здоровый человек» и «нездоровый человек», «инженер» и «человек, инженером не являющийся» и др. Поскольку, согласно закону исключенного третьего, между А и не-А не существует промежуточного звена, положительные и соответствующие им отрицательные понятия всегда исчерпывают объем понятия, которому они подчинены (все люди либо инженеры, либо не-инженеры, «третьего не дано»). 6. Соподчинение имеет место тогда, когда два (или более) несовместимых понятий, не имея общих элементов в объемах, не исчерпывают объем родового для них понятия, которому они подчинены. Особым отношением является отношение соподчинения, когда объемы двух понятий, исключающие друг друга, входят в объем третьего понятия. Например, понятия «автобус» и «трамвай» попадают в одну категорию – «городской транспорт». Иногда соподчиненные понятия внешне выглядят как противоречивые. Это касается тех случаев, когда понятия выделяют классы предметов, находящихся как бы на противоположных краях объема родового понятия, которому они подчинены. Возьмем, например, понятия «отличник» и «двоечник». На первый взгляд, они противоречивы, поскольку отрицают друг друга. Однако анализ их отношения с родовым для них понятием «учащийся» показывает, что отношения противоречия между ними нет. Последнее имело бы место, если бы объем понятия «учащийся» равнялся сумме объемов наших двух понятий. Но в действительности среди учащихся есть еще троечники, хорошисты. Поэтому рассмотренный случай является разновидностью отношения соподчинения, а не противоречия.
Определение понятий Определение (или дефиниция) понятия есть логическая операция, которая раскрывает содержание понятия либо устанавливает значение термина. С помощью определения понятий мы в явной форме указываем на сущность отражаемых в понятии предметов, раскрываем содержание понятия и тем самым отличаем круг определяемых предметов от других предметов. Так, например, давая определение понятия «трапеция», мы отличаем его от других четырехугольников, например от прямоугольника или ромба. «Трапеция — четырехугольник, у которого две стороны параллельны, а две другие — не параллельны» (1). Приведем еще несколько определений понятий, взятых из школьных учебников, которые принадлежат к двум различным видам определений. «Вещества, растворы которых проводят электрический ток, называются электролитами» (2). «Флорой называют видовой состав растений, произрастающих на той или иной территории» (3). «Естественный отбор — процесс выживания наиболее приспособленных особей, который ведет к преимущественному повышению или понижению численности одних особей в популяции по сравнению с другими» (4). В явном определении понятие, содержание которого надо раскрыть, называется определяемым понятием [ definiendum (дефиниендум), сокращенно Dfd ], а то понятие, посредством которого оно определяется, называется определяющим понятием [ definience (дефиниенс), сокращенно — Dfn ].
Реальные и номинальные определения Если определяется понятие, то определение будет реальным. Если определяется термин, обозначающий понятие, то определение будет номинальным. Из вышеприведенных определений (1) и (4)—это реальные определения, а (2) и (3) — номинальные определения. С помощью номинальных определений вводятся также новые термины, краткие имена взамен более сложных описаний предметов. Например, «навыком называют такое действие, в составе которого отдельные операции стали автоматизированными в результате упражнений».
Путем номинальных определений вводятся и знаки, заменяющие термины. Например, «Конъюнкция обозначается знаками ^ или &», «С — скорость света», «Тангенс угла α обозначается как tg α» и т. д. В номинальном определении часто раскрывается и этимология того или иного термина. Например, «Термин «философия» происходит от греческих слов «филео» — люблю и «софия» — мудрость, что означает любовь к мудрости (или, как говорили раньше на Руси, любомудрие)». Для номинальных определений характерно присутствие в их составе слова «называют(ся)». Номинальные определения часто встречаются в учебниках по математике для средней школы. Так, в курсе геометрии встречаются следующие номинальные определения: «Конус называется круговым, если основание его — круг» или «Круглый конус называют конусом вращения». Определения делятся на явные и неявные. Явные определения — это такие, в которых даны Dfd и Dfn и между ними устанавливается некоторое отношение равенства, эквивалентности. Самое распространенное явное определение — определение через ближайший род и видовое отличие. В нем устанавливаются существенные признаки определяемого понятия. Примеры. 1. «Правильный многоугольник — многоугольник, у которого все стороны конгруэнтны и все углы равны». 2. «Барометр — прибор для измерения атмосферного давления». 3. «Гротеск — один из способов сатирического изображения жизни, отличающийся резким преувеличением, сочетанием реального и фантастического». Признак, указывающий на тот круг предметов, из числа которых нужно выделить определяемое множество предметов, называется родовым признаком, или родом. В приведенных примерах родовыми являются понятия «многоугольник», «прибор», «способ сатирического изображения жизни». Признаки, при помощи которых выделяется определяемое множество предметов из числа предметов, соответствующих родовому понятию, называются видовым отличием. При определении понятия видовых признаков (отличий) может быть один или несколько. К явным определениям понятий относятся и генетические определения. Они часто встречаются в школьных учебниках. Генетическим называется определение предмета путем указания на способ, которым образуется только данный предмет и никакой другой (это его видовое отличие). Генетическое определение является разновидностью определения через род и видовое отличие. Приведем примеры генетических определений из области химии. 1. Кислотами называются сложные вещества, образующиеся из кислотных остатков и атомов водорода, способных замещаться атомами металлов или обмениваться на них. 2. Коррозия металлов — это окислительно-восстановительный процесс, образующийся в результате окисления атомов металла и перехода их в ионы.
Правила явного определения. Ошибки, возможные в определении 1. Определение должно быть соразмерным, т. е. объем определяющего понятия должен быть равен объему определяемого понятия. чего возникают логические ошибки в определении. Типы этих логических ошибок: а) широкое определение, когда Dfd<Dfn. Такая ошибка содержится в следующих определениях: «Гравитация — это взаимодействие двух материальных тел». «Лошадь — млекопитающее и позвоночное животное». (Здесь понятие «лошадь» нельзя отличить от понятий «корова» или «коза».) Понятие «окружность» неправильно определяется так: «Это фигура, которая описывается движущимся концом отрезка, когда другой его конец закреплен, или фигура, которая образована движущимся концом циркуля». С помощью этого определения нельзя отличить понятие «окружность» от понятия «дуга», так как не указано, что окружность — это кривая замкнутая линия;
б) узкое определение, когда Dfd>Dfh. Например, «Совесть — это осознание человеком ответственности перед самим собой за свои действия и поступки» (а перед обществом?). «Производительными силами называются орудия труда, а также и сами люди с их умениями и приемами труда». (В производительные силы входят все средства производства, а не только орудия труда.); в) определение в одном отношениии широкое, в другом — узкое. В этих неправильных определениях Dfd>Dfn и Dfd<Dfn (в разных отношениях). Например, «Бочка — сосуд для хранения жидкостей». С одной стороны, это широкое определение, так как сосудом для хранения жидкостей может быть и чайник, и ведро, и т. д.; с другой стороны, это узкое определение, так как бочка пригодна для хранения и твердых тел, а не только жидкостей. Аналогичная ошибка содержится в определении понятия «учитель»: «Учитель — человек, обучающий детей». 2. Определение не должно содержать круга. Круг возникает тогда, когда Dfd определяется через Dfn, a Dfn был определен через Dfd. В определении «Вращение есть движение вокруг своей оси» будет допущен круг, если до этого понятие «ось» было определено через понятие «вращение» («ось — это прямая, вокруг которой происходит вращение»). Круг возникает и тогда, когда определяемое понятие характеризуется через него же, лишь выраженное иными словами, или когда определяемое понятие включается в определяющее понятие в качестве его части. Такие определения носят название тавтологий. Тавтологичны такие определения: «Халатность заключается в том, что человек халатно относится к своим обязанностям»; «Количество — это характеристика предмета с его количественной стороны». Логически некорректным является употребление в мышлении (и в речи) тавтологий, таких, например, как масляное масло, трудоемкий труд, порученное поручение, прогрессирующий прогресс, ладанная задача, изобрету изобретение, поиграем в игру, памятный сувенир, подытожим итоги и др. Иногда можно встретить выражения вида: «Закон есть закон», «Жизнь есть жизнь» и т. д., которые представляют собой прием усиления, а не сообщения в предикате какой-то информации о субъекте, так как субъект и предикат тождественны. Такие выражения не претендуют на определение соответствующего понятия: «закон», «жизнь» или др.
3. Определение должно быть четким, ясным. Это правило означает, что смысл и объем понятий, входящих в Dfn, должен быть ясным и определенным. Определения понятий должны быть свободными от двусмысленности; не допускается подмена их - метафорами, сравнениями и т. д. Не будут определениями следующие суждения: «Архитектура — застывшая музыка», «Лев — царь зверей», «Верблюд — корабль пустыни», «Такт — это разум сердца» (К. Гуцков), «Неблагодарность — род слабости» (И. В. Гёте).
Неявные определения Вотличие от явных определений, имеющих структуру Контекстуальное определение позволяет выяснить содержание незнакомого слова, выражающего понятие, через контекст, не прибегая к словарю для перевода, если текст дан на иностранном языке, или к толковому словарю, если текст дан на родном языке. Значения неизвестных в уравнениях даны в неявном виде. Если дано уравнение, первой степени, например 10— y =3, или дано квадратное уравнение, например х 2 — 7 x +12=0, то, решая их и находя значение корней этих уравнений, мы даем явное определение для у (у =7) и для х (x1 = 4 и х2 = 3). Индуктивные определения характеризуются тем, что определяемый термин используется в выражении понятия, которое ему приписывается в качестве его смысла. Примером индуктивного определения является определение понятия «натуральное число» с использованием самого термина «натуральное число»: 1. 1 — натуральное число. 2. Если n — натуральное число, то n + 1 — натуральное число. 3. Никаких натуральных чисел, кроме указанных в пунктах 1 и 2, нет. С помощью этого индуктивного определения получается натуральный ряд чисел: 1, 2, 3, 4.....Таков алгоритм построения натуральных чисел.
|
||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 547; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.183.89 (0.013 с.) |
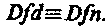 Это правило часто нарушается, в результате,
Это правило часто нарушается, в результате,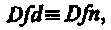 в неявных определениях просто на место Dfn подставляется контекст, или набор аксиом, или описание способа построения определяемого объекта.
в неявных определениях просто на место Dfn подставляется контекст, или набор аксиом, или описание способа построения определяемого объекта.


