
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потери напора по длине в круглой цилиндрической трубе.Содержание книги
Поиск на нашем сайте
Цель работы 1. Ознакомиться с методикой определения потерь напора на длине при движении потока в круглой цилиндрической трубе. 2. Экспериментально определить коэффициент гидравлического трения при движении жидкости в круглых трубах. 3. Сравнить экспериментально полученные значения коэффициента гидравлического трения и его расчетные значения по рекомендуемым формулам в зависимости от режима течения.
Основные сведения из теории При движении жидкости по каналу потери напора принято делить на две части – потери напора на длине Уравнение Бернулли для двух сечений потока имеет вид
Чтобы определить потерю напора на горизонтальном участке трубы постоянного диаметра, не имеющем местных сопротивлений, достаточно определить пьезометрический напор в двух сечениях, тогда
Расчет потерь напора на длине выполняют по формуле
где
При изучении движения в трубах принимают, что коэффициент гидравлического трения зависит от числа Рейнольдса и относительной шероховатости стенки трубы Каждой из четырех зон течения: 1 – зона ламинарного течения, 2 – зона гидравлически
гладкого течения, 3 – зона переходного течения и 4 – зона квадратичного течения соответствуют расчетные формулы (3.4) для определения коэффициента гидравлического трения λ: Оценим соответствие формул (3.4) и графиков Никурадзе. Для чего выполним расчеты по формулам (3.4) и наложим расчетные точки на график Никурадзе. Вот расчеты для двух значений шероховатости: ( Таблица 3.1
Расчеты для третьего значения шероховатости не приводятся, но расчетные точки на графике отображены прерывистыми линиями (см. рис. 3.3).
Рис. 3.3 В переходной зоне, характеризуемой числами Рейнольдса 2300<Re<4000 (3,36<logRe<3,6) имеет место наибольшее расхождение расчетных и экспериментальных данных. Есть расхождения и в зоне переходного и квадратичного течения. Максимальное расхождение расчетных и экспериментальных значений λ достигает 30%. Это необходимо принимать во внимание, оценивая результаты лабораторного эксперимента.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 173; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.1.100 (0.008 с.) |

 и местные потери
и местные потери  .
.


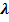 -- коэффициент гидравлического трения (или коэффициент Дарси);
-- коэффициент гидравлического трения (или коэффициент Дарси); – длина участка трубы между сечениями;
– длина участка трубы между сечениями; -- диаметр трубы.
-- диаметр трубы. , где
, где  -- среднее значение шероховатости. Результаты опытов И. Никурадзе для круглых труб представлены на рис. 3.2.
-- среднее значение шероховатости. Результаты опытов И. Никурадзе для круглых труб представлены на рис. 3.2. если Re ≤ 2300;
если Re ≤ 2300;
 если 2300 ≤Re ≤
если 2300 ≤Re ≤  ;
;
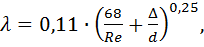 если
если  ;
;
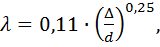 если
если  ;
;
 )=30, (
)=30, (


