
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение неразрывности элементарной струйки идеальной жидкости.Содержание книги
Поиск на нашем сайте
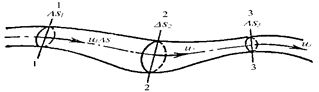
Рассмотрим элементарную струйку несжимаемой жидкости при установившемся движении. Выделим сечение 1-1 и 2-2, расположенные на расстоянии l одно от другого (рис.1.23). Здесь Δ s1 и Δ s2 - площади живых сечений соответственно; u 1 и u2 - скорости; Δ Q 1 и ΔQ2 - расходы элементарной струйки в сечениях.
Очевидно, что Δ Q1 = Δs1u 1 и Δ Q2 = Δs2u 2, причем Δ Q 1 втекает в рассматриваемый отсек, а Δ Q 2 - вытекает. Учитывая, что форма элементарной струйки не изменяется с течением времени, поперечный приток и отток невозможен, так как скорости на боковой поверхности струйки направлены по касательным к линиям тока, из которых состоит эта боковая поверхность, получаем, что расходы Δ Q 1 и ΔQ2 равны, т.е. Δs1u 1 = Δs2u2. Аналогичные соотношения можно написать для любых двух сечений элементарной струйки, расположенных вдоль нее: u 1 Δs1 = u2Δs2 =...= uΔs = ΔQ = const. Это и есть уравнение неразрывности для элементарной струйки несжимаемой жидкости при установившемся движении. Если выделить в потоке два любых сечения, отстоящих на некотором расстоянии, то, просуммировав по каждому из живых сечений обе части в уравнении
Таким образом, в отмеченных условиях расход, проходящий через все живые сечения потока, неизменен, несмотря на то что в каждом сечении средняя скорость и площадь живого сечения могут быть различны.
2. Кач-нное влиян темп на вязкость жидк и газа. В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры. Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 364; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.184 (0.008 с.) |

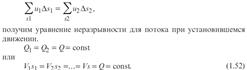
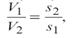 т.е. средние скорости обратно пропорциональны площадям живых сечений потока, которым соответствуют эти средние скорости.
т.е. средние скорости обратно пропорциональны площадям живых сечений потока, которым соответствуют эти средние скорости.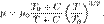 где: μ = динам вязкость в (Па·с) при заданной темп T, μ0 = контрольная вязкость в (Па·с) при некоторой контрольной темп T0, T = заданная темп в К, T0 = контрольная темп в К, C = постоянная Сазерленда для того газа, вязкость которого требуется определить. Эту формулу можно применять для темп в диапазоне 0 < T < 555 K и при давлениях менее 3,45 МПа с ошибкой менее 10%, обусловленной зависимостью вязкости от давления. Вязкость жидкостей. Динамический коэффициент вязкости. Внутреннее трение жидкостей, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Справедлив общий закон внутреннего трения — закон Ньютона:
где: μ = динам вязкость в (Па·с) при заданной темп T, μ0 = контрольная вязкость в (Па·с) при некоторой контрольной темп T0, T = заданная темп в К, T0 = контрольная темп в К, C = постоянная Сазерленда для того газа, вязкость которого требуется определить. Эту формулу можно применять для темп в диапазоне 0 < T < 555 K и при давлениях менее 3,45 МПа с ошибкой менее 10%, обусловленной зависимостью вязкости от давления. Вязкость жидкостей. Динамический коэффициент вязкости. Внутреннее трение жидкостей, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Справедлив общий закон внутреннего трения — закон Ньютона: 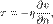 Коэф вязкости
Коэф вязкости  (динамическая вязкость) может быть получен на основе соображений о движениях молекул.
(динамическая вязкость) может быть получен на основе соображений о движениях молекул. 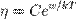 . Иная формула, представляющая коэф вязкости, была предложена Бачинским. Как показано, коэф вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества
. Иная формула, представляющая коэф вязкости, была предложена Бачинским. Как показано, коэф вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества 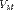 . Эксперименты показали, что между молярным объёмом и коэф вязкости сущ-ет соотношение
. Эксперименты показали, что между молярным объёмом и коэф вязкости сущ-ет соотношение 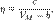 где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского. Динамическая вязкость жидкостей уменьшается с увеличением температуры, и растёт с увеличением давления. Кинематическая вязкость. В технике, часто приходится иметь дело с величиной
где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского. Динамическая вязкость жидкостей уменьшается с увеличением температуры, и растёт с увеличением давления. Кинематическая вязкость. В технике, часто приходится иметь дело с величиной 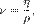 и эта величина получила название кинематической вязкости. Здесь
и эта величина получила название кинематической вязкости. Здесь 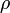 — плотность жидкости;
— плотность жидкости;  1c = 10-6 м2
1c = 10-6 м2  где
где 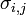 — тензор вязких напряжений. Среди неньютоновских жидкостей, по зависимости вязкости от скорости деформации различают псевдопластики и дилатантные жидкости. Моделью с ненулевым напряжением сдвига (действие вязкости подобно сухому трению) является модель Бингама. Если вязкость меняется с течением времени, жидкость называется тиксотропной.
— тензор вязких напряжений. Среди неньютоновских жидкостей, по зависимости вязкости от скорости деформации различают псевдопластики и дилатантные жидкости. Моделью с ненулевым напряжением сдвига (действие вязкости подобно сухому трению) является модель Бингама. Если вязкость меняется с течением времени, жидкость называется тиксотропной.


