
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет параметров системы синхронизации с добавлением и
Вычитанием импульсов
Дано: Решение
т.к. при В=9600 Бод tп.с =20.8<1 мин, следовательно спустя минуту ошибки будут возникать.
Таблица 1 Зависимость tп.с, от В
Задача №2 В СПД используется устройства синхронизации без непосредственного воздействия на частоту задающего генератора. Скорость модуляции равна В. Шаг коррекции должен быть не более Dj. Определить частоту задающего генератора (ЗГ) и число ячеек делителя частоты, если коэффициент деления каждой ячейки равен 2. Значения В и Dj определяются по формулам:
В=1000+10N=1020 Dj=0.01+0.003N=£0.016 dк£Dj fзг-?, n-? Решение
Ответ: n=6; fзг=65.28, кГц
Задача №3 Рассчитать параметры устройства синхронизации без непосредственного воздействия на частоту ЗГ со следующими характеристиками: время синхронизации не более 1с, время поддержания синфазности не менее 10 с, погрешность синхронизации не более 10% единичного интервала t0. Среднеквадратичное значение краевых искажений равно 10%t0, исправляющая способность m=45%, коэффициент нестабильности генераторов K=10’6. Значение В определяется по формуле:
В=(600+ 10N), Бод. Дано: Решение
Т.к.
где eдин=0.037
Ответ: S=25; m=17; fзг=10.5 кГц
Задача №4 Определить реализуемо ли устройство синхронизации без непосредственного воздействия на частоту ЗГ обеспечивающее погрешность синхронизации e=2.5% при условиях предыдущей задачи.
Вывод: т.к. емкость реверсивного счетчика отрицательна, то устройство не реализуемо.
Задача №5 В СПД используется устройство синхронизации без непосредственного воздействия на частоту ЗГ с коэффициентом нестабильности К=0,00001.Коэффициент деления делителя m=10. емкость реверсивного счетчика S=10. Смещение ЗМ подчинено нормальному закону с нулевым математическим ожиданием и СКО равным dкр.и=(15+N/2)% длительности единичного интервала. Рассчитать вероятность ошибки при регистрации элементов методом стробирования без учета и с учетом погрешности синхронизации. Исправляющую способность приемника считать равной 50%.
Дано: Решение
Откуда:
2. Без учета e (e=0):
Ответ: Кодирование в системах ПДС
Классификация кодов Известно большое число помехоустойчивых кодов, которые классифицируются по различным признакам. Помехоустойчивые коды можно разделить на два больших класса: блочные и непрерывные. При блочном кодировании последовательность элементарных сообщений источника разбивается на отрезки и каждому отрезку ставится в соответствие определенная последовательность (блок) кодовых символов, называемая обычно кодовой комбинацией. Множество всех кодовых комбинаций, возможных при данном способе блочного кодирования, и есть блочный код. Длина блока может быть как постоянной, так и переменной. Различают равномерные и неравномерные блочные коды. Помехоустойчивые коды являются, как правило, равномерными. Блочные коды бывают разделимыми и неразделимыми. К разделимым относятся коды, в которых символы по их назначению могут быть разделены на информационные символы, несущие информацию о сообщениях и проверочные. Такие коды обозначаются как (n, k), где n - длина кода, k - число информационных символов. Число комбинаций в коде не превышает 2 ^k. К неразделимым относятся коды, символы которых нельзя разделить по их назначению на информационные и проверочные. Коды с постоянным весом характеризуются тем, что их кодовые комбинации содержат одинаковое число единиц: Примером такого кода является код “3 из 7”, в котором каждая кодовая комбинация содержит три единицы и четыре нуля (стандартных телеграфный код № 3).
Коды с постоянным весом позволяют обнаружить все ошибки кратности q=1,...,n за исключением случаев, когда число единиц, перешедших в нули, равно числу нулей, перешедших в единицы. В полностью асимметричных каналах, в которых имеет место только один вид ошибок (преобразование нулей в единицы или единиц в нули), такой код дозволяет обнаружить все ошибки. В симметричных каналах вероятность необнаруженной ошибки можно
 определить как вероятность одновременного искажения одной единицы и одного нуля:
где Pош вероятность искажения символа. Среди разделимых кодов различают линейные и нелинейные. К линейным относятся коды, в которых поразрядная сумма по модулю 2 любых двух кодовых слов также является кодовым словом. Линейный код называется систематическим, если первые k символов его любой кодовой комбинации являются информационными, остальные (n- k) символов — проверочными.
Подклассом линейных кодов являются циклические коды. Они характеризуются тем, что все наборы, образованные циклической перестановкой любой кодовой комбинации, являются также кодовыми комбинациями. Это свойство позволяет в значительной степени упростить кодирующее и декодирующее устройства, особенно при обнаружении ошибок и исправлении одиночной ошибки. Примерами циклических кодов являются коды Хэмминга, коды Боуза - Чоудхури - Хоквингема (БЧХ — коды) и др. Примером нелинейного кода является код Бергера, у которого проверочные символы представляют двоичную запись числа единиц в последовательности информационных символов. Например, таким является код: 00000; 00101; 01001; 01110; 10001; 10110; 11010; 11111. Коды Бергера применяются в асимметричных каналах. В симметричных каналах они обнаруживают все одиночные ошибки и некоторую часть многократных. Непрерывные коды характеризуются тем, что операции кодирования и декодирования производятся над непрерывной последовательностью символов без разбиения ее на блоки. Среди непрерывных, наиболее применимы сверточные коды. Как известно, различают каналы с независимыми и группирующимися ошибками. Соответственно помехоустойчивые коды можно разбить на два класса: исправляющие независимые ошибки и исправляющие пакеты ошибок. Далее будут рассматриваться в основном коды, исправляющие независимые ошибки. Это объясняется тем, что хотя для исправления пакетов ошибок разработано много эффективных кодов, на практике целесообразнее использовать коды, исправляющие независимые ошибки вместе с устройством перемежения символов или декорреляции ошибок. При этом символы кодовой комбинации не передаются друг за другом, перемешиваются с символами других кодовых комбинаций. Если интервал между символами, принадлежащими одной кодовой комбинации, сделать больше чем “память” канала, то ошибки в пределах кодовой комбинации можно считать независимыми, что и позволяет использовать коды, исправляющие независимые ошибки.
Циклические коды Циклические коды относятся к классу линейных систематических. Поэтому для их построения в принципе достаточно знать порождающую матрицу.
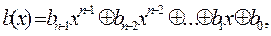 Можно указать другой способ построения циклических кодов, основанный на представлении кодовых комбинаций многочленами b(х) вида:
где bn-1bn-2...bo - кодовая комбинация. Над данными многочленами можно производить все алгебраические действия с учетом того, что сложение здесь осуществляется по модулю 2. Каждый циклический код (n, k) характеризуется так называемым производящим многочленом. Им может быть любой многочлен р(х) степени n-k. Циклические коды характеризуются тем, что многочлены b(x) кодовых комбинаций делятся без остатка на р(х). Поэтому процесс кодирования сводится к отысканию многочлена b(x) по известным многочленам a(х) а р(х), делящегося на р(х), где a(х)- многочлен степени k-1, соответствующий информационной последовательности символов. Очевидно, что в качестве многочлена b(x) можно использовать произведение a(х)р(х). Однако при этом информационные и проверочные символы оказываются перемешанными, что затрудняет процесс декодирования. Поэтому на практике в основном применяется следующий метод нахождения многочлена b(x). Умножим многочлен а(х) на и полученное произведение разделим на р(х). где m(х) - частное, а с(х) - остаток:
Так как операции суммирования и вычитания по модулю 2 совпадают, то выражение перепишем в виде:
Из этой формулы следует, что многочлен Многочлен

В качестве примера приведена схема кодера и декодера для кода (9,5) (см. рис.11) с порождающим многочленом: Код имеет кодовое расстояние d0= 4, что позволяет ему исправлять все однократные ошибки ( За 9 тактов происходит деление принятых комбинаций на образующий полином. После 9 такта в ячейках ФПГ готов остаток, если ошибок нет он нулевой, тогда на выходе схемы «или» будет «0» и при замыкании ключа стирания принятой комбинации не будет. Если в ячейке ФПГ есть хотя бы одна единица, значит, была ошибка, на выходе схемы ФПГ будет «1», которая в момент замыкания ключа поступит на вход R (RESET) и сотрет принимаемую комбинацию. По этому же сдвигу формируется запрос на повторную передачу (ФСОС). Существуют и другие, более универсальные, алгоритмы декодирования. К циклическим кодам относятся коды Хэмминга, которые являются примерами немногих известных совершенных кодов. Они имеют кодовое расстояние d=3 и исправляют все одиночные ошибки. Среди циклических кодов широкое применение нашли коды Боуза- Чоудхури- Хоквингема (БЧХ). Рассмотрим по подробнее понятие синдрома в циклических кодах, а также их свойства. Синдром циклического кода, как в любом систематическом коде, определяется суммой по модулю 2, принятых проверочных элементов и элементов проверочной группы, сформированных их принятых элементов информационной группы В циклическом коде для определения синдрома следует разделить принятую кодовую комбинацию на кодовую комбинацию производящего полинома. Если все элементы приняты правильно, остаток от деления R(x) равен нулю. Наличие ошибок приводит к тому, что R(x)≠0. Следовательно, синдром циклического кода является многочлен R(x). Для определения номеров элементов, в которых произошла ошибка, существует несколько методов. Один из них основан на свойстве, которое заключается в том, что R(x), полученный при делении принятого многочлена H(x) на Pr(x), равен R(x), полученному в результате деления соответствующего многочлена ошибок E(x) на Pr(x). Многочлен ошибок E(x)= H(x)+ А(x), где A(x) – исходный многочлен циклического кода. Так, если ошибка произошла в а1, то при коде (9.5) E1(0,1)=100000000, ошибка а2 соответствует E2(0,1)=010000000 и т.д. Остаток от деления E(0,1) на Pr(0,1)=10011= R1(0,1) для заданного 9 элементного кода всегда одинаков, он не зависит от вида передаваемой комбинации. В рассматриваемом примере R(0,1)=0101. Наличие ошибок в других элементах (а2, а3,…) приведет к другим остаткам. Остатки зависят только вида Pr(x) и n. Для n = 9 и P4(0,1) = 10011 будет следующее соответствие:
Таблица 2 Анализ синдрома
Указанное однозначное соответствие можно использовать для определения места ошибки. Синдром не зависит от переданной кодовой комбинации, но в нем сосредоточена вся информации о наличии ошибок. Обнаружение и исправление ошибок в систематических кодах может быть только на основе анализа синдрома. На основании приведенного свойства существует следующий способ определения места ошибки. Сначала определяют остаток R1(0,1), соответствующий наличию ошибки в старшем разряде. Если ошибка произошла в следующем разряде (более низком), то такой же остаток получится в произведении принятого многочлена и х, т.е. H(x)x.
Рассмотрим построение кодовой комбинации циклического кода. Пусть дано: 1.Исходная KK, поступающая от источника А(х), содержит k элементов. 2. Дан производящий полином Pr(x), где r -число проверочных элементов. Задание: сформировать KK ЦК. Формирование KK производится по следующему алгоритму: 1.А(х)умножается на хr. 2. Полученное произведение делим на Рr(х). В результате получим:
3. У множим правую и левую части на Рr(х). В результате:
А(х)×хr=G(х)×Pr(x)+R(x) (суммирование производится по мод. 2) (3.7)
4. Перенесем A(x)×xrв правую часть уравнения, a G(x)×P(x) в левую, в результате:
G(x)×P(x)=A(x)×xr+R(x) (суммирование по мод. 2) (3.8) Левая часть делится на Рr(x) без остатка, а следовательно, должна делится без остатка и правая часть. Существует два способа формирования КК ЦК: 1.Умножение исходной КК наРr(х). Недостатком этого способа является получение неразделимого ЦК, т.е. нельзя выделить отдельно информационные и проверочные элементы. 2. Деление на производящий полином (способ, алгоритм которого описан выше). В этом случае код получается разделимым.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.86.138 (0.047 с.) |
 , e=0 т.к. краевые искажения отсутствуют =>
, e=0 т.к. краевые искажения отсутствуют => 


 ;
;  ;
;  ;
; , Гц
, Гц

 , где
, где  ;
; =>
=>  , тогда:
, тогда:

 , Гц
, Гц

 , где
, где 
 , где
, где  , где:
, где: 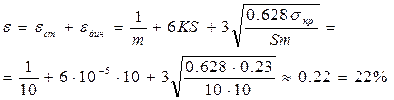

 ;
; 

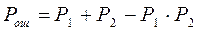
 , где
, где 
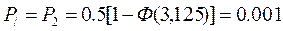 ;
; 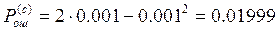
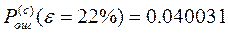 ,
, 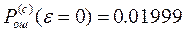



 делится на р(х) и, следовательно, является искомым.
делится на р(х) и, следовательно, является искомым. имеет следующую структуру: первые n-k членов низшего порядка равны нулю, а коэффициенты остальных совпадают с соответствующими коэффициентами информационного многочлена а(х). Многочлен с(х) имеет степень меньше n-k. Таким образом, в найденном многочлене b(x) коэффициенты при х в степени n-k и выше совпадают с информационными символами, а коэффициенты при остальных членах, определяемых многочленом с(х), совпадают с проверочными символами. На основе приведенных схем умножения и деления многочленов и строятся кодирующие устройства для циклических кодов.
имеет следующую структуру: первые n-k членов низшего порядка равны нулю, а коэффициенты остальных совпадают с соответствующими коэффициентами информационного многочлена а(х). Многочлен с(х) имеет степень меньше n-k. Таким образом, в найденном многочлене b(x) коэффициенты при х в степени n-k и выше совпадают с информационными символами, а коэффициенты при остальных членах, определяемых многочленом с(х), совпадают с проверочными символами. На основе приведенных схем умножения и деления многочленов и строятся кодирующие устройства для циклических кодов.
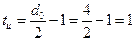 ).
). (3.6)
(3.6)


