
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема 6. Появление молчащих рецепторов в ткани.Содержание книги
Поиск на нашем сайте
А. Изначально ткань содержит 4 рецептора и 4 эффектора, поэтому величина ЕС50 для нее равна 2 ЕД лекарства и доза при которой лекарство занимает 50% рецепторов также составляет 2 ЕД. В. При увеличении числа рецепторных молекул в 5 раз (20 молекул) с прежним числом эффекторов (4 молекулы) возникает ситуация, когда лекарству по-прежнему, чтобы вызвать 50% эффект достаточно 2 ЕД, но чтобы занять 50% рецепторов требуется 10 ЕД. Наличие молчащих рецепторов имеет место в миокарде, где число b1-адренорецепторов в 10 раз превосходит число эффекторных молекул, связанных с ними. Избыточность b1-адренорецепторов имеет важное значение и позволяет миокарду в полной мере реагировать на медиаторы (норадреналин и адреналин) даже после того, как большая часть рецепторов будет утрачена. Описывая и разбирая процедуру построения кривой «доза-эффект», мы исходили из предположения о том, что эффект лекарства является непрерывной величиной, которая может быть измерена количественно. Например, гипотензивный эффект лекарства может быть измерен по уровню артериального давления, жаропонижающий эффект – по степени снижения температуры тела. Такие эффекты носят название градуальных (непрерывных, интегральных), а кривые, которые описывают такой эффект получили название градуальных кривых «доза-эффект». К сожалению, некоторые эффекты лекарств являются дискретной величиной или качественным признаком, т.е. они описываются всего лишь несколькими вариантами состояния. Например, головная боль может либо быть, либо отсутствовать у конкретного пациента, контрацептивный эффект лекарства либо проявляется, либо нет. Такие эффекты лекарств называют квантовыми или дискретными. Для квантового эффекта не возможно построить кривую зависимости величины эффекта от дозы для каждого конкретного индивидуума. Чтобы избежать возникшего затруднения прибегают к построению квантовой кривой «доза-эффект», где отмечают зависимость проявления эффекта в популяции от величины принимаемой дозы лекарства. Вначале при введении небольших доз эффект развивается у малого числа объектов. По мере повышения дозы на лекарство начинает реагировать все большее число испытуемых и наконец остается лишь небольшая группа объектов у которой реакцию удается вызвать применяя высокие дозы лекарства. График зависимости «доза-эффект» при этом имеет куполообразный вид и идентичен Гауссовой кривой нормального распределения (см. схему 7). Величина соответствующая куполу кривой позволяет определить активность лекарства – т.е. ту его дозу, которая вызывает развитие эффекта у 50% лиц в популяции.
Схема 7. Квантовые кривые «доза-эффект». Левая кривая представляет построение зависимости для терапевтического эффекта лекарства, а правая – развитие токсического эффекта (смерти) после введения летальных доз лекарства. Как следует из графика доза в 1,25 и 2,5 мг вызывают эффект у незначительного количества животных, однако введение лекарства в дозе 5 мг позволяет вызвать эффект у наибольшего числа особей, оставшееся небольшое число животных реагируют на высокие доза лекарства. Аналогичные рассуждения справедливы и для введения летальных доз лекарства. Таким образом, квантовая кривая «доза эффект» может помочь установить величину ЕС50, но ничего не говорит об эффективности лекарства. Если на графике зависимости отмечать не то число объектов, у которого удалось получить ответ на каждую дозу в отдельности, а накопленное число объектов – т.е. всех лиц у которых к моменту введения дозы уже удалось добиться эффекта и пациентов прореагировавших на данную дозу, то кривая может быть трансформирована в стандартную S-образную форму, напоминающую градуальную кривую. Однако, эта кривая не будет нести никакой дополнительной информации. Таблица 1. Различия между градуальной и квантовой кривыми «доза-эффект»
Широта терапевтического действия. Терапевтический индекс. Терапевтический коридор.
Если после того, как достигается плато эффекта доза лекарства будет продолжать расти, то через определенный промежуток времени начнет проявляться токсическое действие лекарства. Зависимость токсического действия от дозы (концентрации) лекарства носит такой же характер, как и его полезный эффект и может быть описана градуальной или квантовой кривыми. На этих кривых также может быть определена величина TD50 или ТС50 – токсической дозы (концентрации) лекарства, которая вызывает токсический эффект, равный 50% от максимального (для квантовой кривой – токсический эффект у 50% лиц в популяции). Иногда, вместо TD50 пользуются показателем LD50 – летальная доза, которая вызывает гибель 50% объектов в популяции. Информация относительного токсического потенциала лекарства позволяет дать характеристику его безопасности. Основными критериями безопасности являются: º Терапевтический индекс – это соотношение между токсической и эффективной дозами лекарства, которые вызывают появление полумаксимального эффекта. ТИ=TD50/ED50. Чем больше величина терапевтического индекса, тем более безопасным является лекарство. Например, на схеме 6 величина ED50»6 мг, а LD50»210 мг и ТИ=210/6=35. Пенициллин является лекарством у которого величина терапевтического индекса составляет более 100, а дигоксин имеет терапевтический индекс равный всего лишь 2. Таким образом, фактически терапевтический индекс определяет расстояние между точками ED50 и TD50 на кривых «доза-эффект». При этом мы исходим из допущения о том, что сами кривые имеют одинаковый наклон и характер нарастания эффекта, а также, что токсическое действие лекарства проявляется позже его терапевтического эффекта. К сожалению, достаточно часто характер кривых терапевтического и токсического действия лекарства будет различаться. º Терапевтическая широта (терапевтическое окно) – это диапазон доз между минимальной терапевтической и минимальной токсической дозами лекарства (ТШ=TD10/ED10). Терапевтическая широта более корректный показатель безопасности лекарства, поскольку он позволяет учитывать степень нарастания нежелательных эффектов на кривой «доза-эффект». Например, на схеме 8 показано лекарственное средство, у которого фармакологическое действие проявляется в виде быстро нарастающего эффекта в ответ на незначительное повышение дозы. Токсическое действие у него, напротив, имеет вид плавно нарастающей кривой. В данном случае величина терапевтического индекса составляет около 10, но благодаря тому, что токсические эффекты нарастают медленно и одновременно с терапевтическим действием 15% эффект лекарства возникает одновременно с развитием отравления у 15% пациентов. Т.е. терапевтическая широта у данного средства отсутствует и его полезное действие возникает одновременно с токсическим. º Фактор надежной безопасности – это отношение минимальной токсической дозы к максимальной эффективной (ФНБ=TD1/ED99). Фактически, данный критерий представляет собой несколько модифицированную форму терапевтической широты и показывает: во сколько раз может быть превышена терапевтическая доза лекарства без риска развития интоксикации (нежелательных эффектов). º Терапевтический коридор – это диапазон эффективных концентраций лекарственного вещества в крови, которые необходимо создать и поддерживать в организме, чтобы обеспечить достижение желаемого терапевтического действия.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.31.178 (0.005 с.) |


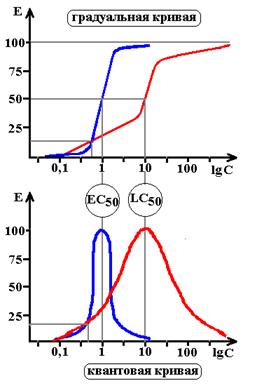 Схема 8. Терапевтический индекс и широта действия. Терапевтический эффект лекарства проявляется с высокой скоростью и EC50=1, токсические эффекты нарастают медленно, при этом LC50=10. Несмотря на то, что ТИ=10/1=10, терапевтическая широта равна нулю, т.к. TD15=LD15=0,6
Схема 8. Терапевтический индекс и широта действия. Терапевтический эффект лекарства проявляется с высокой скоростью и EC50=1, токсические эффекты нарастают медленно, при этом LC50=10. Несмотря на то, что ТИ=10/1=10, терапевтическая широта равна нулю, т.к. TD15=LD15=0,6



