
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула взаимосвязи производной по направлению и градиентаСодержание книги
Поиск на нашем сайте
Доказательство. Обозначим координаты вектора
Это функция Рассмотрим производную композиции функций Производная внешней функции (которая действует последняя) это вектор-строка градиент функции f. Производная внутренней функции (которая действует первая) это вектор-столбец.
Но ведь
Но это и есть скалярное произведение градиента и вектора
Отсюда виден смысл градиента. Геометрический смысл. Градиент это вектор, при движении в направлении которого рост функции наиболее быстрый. Если движение в перпендикулярном направлении, то рост функции будет нулевым. Если под большим увеличением рассмотреть какой-то небольшой кусочек поверхности, то он выглядит почти как наклонная плоскость, а для наклонной плоскости при движении в ту сторону, куда она наклонена, наибольшая скорость роста высоты, в перпендикулярном направлении - высота не изменяется, а при движении в противоположном - уменьшается. Замечание. Если направление
Лекция № 13. 02. 12. 2016 Теорема. Пусть кривая неявно задана уравнением Доказательство. Кривая также может быть задана и параметрически. Тогда получается функция
Геометрический смысл: сечение поверхности, наибольший рост ортогонален сечению. Пример: Если на склоне горы двигаться к вершине, то на карте движение будет видно как ортогональное линии уровня. Теорема. Пусть поверхность неявно задана уравнением Доказательство. Рассмотрим произвольную кривую, которая целиком лежит на поверхности. Её можно задать параметрическими уравнениями: Вектор, лежащий на касательной к этой кривой в точке Так как
Тогда и её производная по t тоже тождественный 0.
но ведь это и есть скалярное произведение векторов Получается, что
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

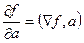 .
. . Точка M произвольная, её координаты
. Точка M произвольная, её координаты 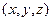 , а точка
, а точка 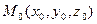 . Так как
. Так как 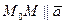 то их координаты пропорциональны, то есть
то их координаты пропорциональны, то есть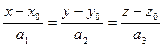 , что также записывается в параметрическом виде:
, что также записывается в параметрическом виде: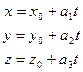
 .
.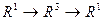 , а именно
, а именно  . Одно число (время t) сначала отображается в тройку чисел (координаты точки в момент времени) а затем функция f отображает эти 3 числа снова в одно число.
. Одно число (время t) сначала отображается в тройку чисел (координаты точки в момент времени) а затем функция f отображает эти 3 числа снова в одно число.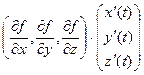
 , аналогично
, аналогично 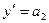 и
и 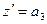 . Тогда
. Тогда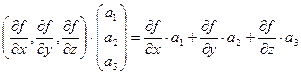
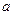 .
. , скалярное произведение этого вектора и градиента
, скалярное произведение этого вектора и градиента  это
это =
= 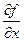 .
.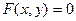 , точка
, точка 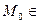 кривой. Тогда градиент
кривой. Тогда градиент 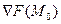 ортогонален этой кривой.
ортогонален этой кривой. , то есть F в итоге есть функция от t, она получается тождественно равной 0. Тогда и её производная по t тоже тождественный 0.
, то есть F в итоге есть функция от t, она получается тождественно равной 0. Тогда и её производная по t тоже тождественный 0.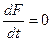 . Запишем по формуле полной производной:
. Запишем по формуле полной производной: . Но ведь это и есть скалярное произведение векторов
. Но ведь это и есть скалярное произведение векторов 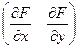 и
и 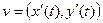 .
. , точка
, точка  .
.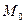 , это
, это 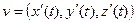 - вектор, который в физике называется вектором скорости. Заметим, что все такие касательные векторы для кривых, лежащих на данной поверхности и проходящих через
- вектор, который в физике называется вектором скорости. Заметим, что все такие касательные векторы для кривых, лежащих на данной поверхности и проходящих через 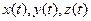 такие, что точка принадлежит поверхности при любом t, то
такие, что точка принадлежит поверхности при любом t, то , то есть F, как функция от t, получается тождественно равной 0.
, то есть F, как функция от t, получается тождественно равной 0.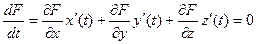
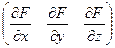 и
и  , то есть градиент ортогонален к касательной для любой кривой, проходящей через точку
, то есть градиент ортогонален к касательной для любой кривой, проходящей через точку 


