
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
VIII. Закон гагена – пуазейля и следствия из него.Содержание книги
Поиск на нашем сайте
Этот закон устанавливает связь между объемным расходом (Q) ламинарно текущей жидкости, видом этой жидкости, а так же геометрическими характеристиками трубки тока. В 1839 г. Гаген, а затем в 1841 г. Пуазейль независимо друг от друга установили, что объемный расход ламинарно текущей жидкости (Q=V/t) прямопропорционален разности давлений на концах трубки тока и радиусу этой трубки в «4-ой» степени и обратно пропорционален длине трубки и коэффициенту динамической вязкости.
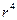 /l·h Þ - закон Гагена-Пуазейля. /l·h Þ - закон Гагена-Пуазейля.
Следствия: ! 10 Т.к Q~
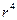 ) /h·l V/t=(p/8)·(∆ p· ) /h·l V/t=(p/8)·(∆ p· 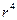 /h·l) /h·l)
V=S·l p·r²u=(p/8)(∆p· S=pr²
30 Время прохождения равных объемов жидкостей через трубки одинакового сечения тем больше, чем больше вязкость жидкости.
V/t1=(p/8)·(∆p·
η1/t1=(π/8)·(∆p·
40 Расстояния, пройденные одинаковыми объемами разных жидкостей по капиллярам одного сечения обратно пропорциональны их вязкости.
V/t=(π/8)·(∆p· l1·η1=(π/8)·(∆p·
IX. НЬЮТОНОВСКИЕ И НЕНЬЮТОНОВСКИЕ ЖИДКОСТИ, ИХ ВИДЫ И ХАРАКТЕРИСТИКА. Ньютоновскими называются жидкости, которые подчиняются уравнению Ньютона (вода). Для них «h» не зависит от градиента скорости «g». Коэффициент вязкости является постоянным и зависит от вида жидкости и от температуры (т.е. увеличением температуры вязкость уменьшается). Неньютоновскими называются жидкости, которые не подчиняются уравнению Ньютона (кровь, эмульсии). Для них вязкость зависит от режима течения и градиента скорости. Эти жидкости состоят из сложных частиц и крупных молекул. Благодаря сцеплению частиц, в них образуются пространственные структуры. Увеличение вязкости происходит потому, что при течении этих жидкостей работа внешней силы затрачивается параллельно и на разрушение структурных образований жидкостей. Т.о. неньютоновские жидкости начинают течь не сразу. Минимальное напряжение сдвига, при котором начинается их течение, называется пределом текучести «t0». Свойства ньютоновских и неньютоновских жидкостей оцениваются с помощью реограмм. Это графики зависимости напряжения сдвига «t», от градиента скорости «g», и коэффициента вязкости «h» от градиента скорости «g». НЬЮТОНОВСКИЕ ЖИДКОСТИ
для воды
нет предела текучести “h” не зависит от “ Неньютоновские жидкости имеют 3 разновидности: а) Пластические – обладают пределом текучести t0, коэффициент вязкости h не зависит от градиента скорости
t0
б ) Псевдопластические – имеют предел текучести “t0”, коэф. вязкости зависит от градиента скорости: он уменьшается до определенного значения, а затем остается постоянным.
t0
в) Дилетантные – имеют предел текучести t0 коэф. вязкости увеличивается с увеличением градиента скорости, а затем не изменяется.
t0
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-18; просмотров: 968; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

 ! 20 Линейная скорость течения жидкости «u» будет прямопропорциональна квадрату радиуса трубки «r²».
! 20 Линейная скорость течения жидкости «u» будет прямопропорциональна квадрату радиуса трубки «r²».


 Q=V/t S·l/t=(p/8)(∆p·
Q=V/t S·l/t=(p/8)(∆p· 
 η1/t1=η2/t2
η1/t1=η2/t2 l1·η1=l2·η2
l1·η1=l2·η2
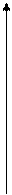 t h
t h для глицерина
для глицерина
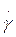 0
0 
 t h
t h
 0
0 

 0
0 

 0
0 


