
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка линейности усилителя вертикального отклонения.Содержание книги
Поиск на нашем сайте
1. Подключите вольтметр параллельно ЗГ и осциллографу (Рис. 7). Обратите внимание на соединительный провод от осциллографа к звуковому генератору. Этот провод часто содержит входной делитель напряжения 1:10. В этом случае измеренное напряжение необходимо умножить на 10 (коэффициент 10 в формуле (1).
Рис. 7. Схема включения осциллографа
2. Установите синусоидальную форму сигнала ЗГ. Изменяя выходное напряжение ЗГ U в от 0 до 5В, измерьте напряжение U 0с помощью осциллографа, для чего измерьте отклонение луча L по оси Y (двойную амплитуду) в делениях шкалы. 3. Рассчитайте напряжение на входе Y осциллографа U0 по формуле (1)
где k - цена деления шкалы осциллографа, на которую установлен переключатель делителя напряжения (рис.6). 4. Результаты измерений занесите в табл. 2. 5. Постройте график зависимости U 0 от U в. Таблица 2
Для построения графика можно воспользоваться методом наименьших квадратов. Зависимость U 0 от U в - линейная: U 0 = g U в. Коэффициент g рассчитайте по формуле (2)
Задание 3. Измерение частоты сигнала по фигурам Лиссажу
1. Ha вход У подайте напряжение 12 Всчастотой f = 50 Гц, (розетка расположена на вертикальной стенке модуля МО-З). На вход Х - от ЗГ. Отключите развертку осциллографа выключателем (13). 2. Отрегулируйте чувствительность осциллографа и напряжение на выходе генератора так, чтобы луч не выходил за пределы экрана. 3. Изменяя частоту ЗГ, добейтесь устойчивой картины на экране осциллографа (Рис.8). 4. Найдите 5-6 различных частот ЗГ, при которых наблюдается устойчивая картина. Занесите в табл.3 форму и число пересечений nx и ny фигур Лиссажу с осями X и Y. 5. Рассчитайте по формуле (3) частоту сигнала, приняв частоту fy =50 Гц. Сравните полученный результат с показаниями шкалы звукового генератора (ЗГ). Результаты занесите в табл. 3.
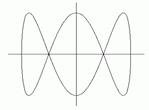
Рис. 8. Сложение взаимно-перпендикулярных колебаний. Фигуры Лиссажу
Таблица 3
Задания для отчета
1. Назначение и устройство осциллографа. 2. Измерения, которые можно проводить с помощью осциллографа. 3. Устройство и принцип действия электронно-лучевой трубки. 4. Как получить на экране осциллографа прямую вертикальную линию? 5. Как получить на экране осциллографа горизонтальную линию? 6. Как получить на экране развертку сигнала? 7. Наблюдение сложения взаимно-перпендикулярных колебаний с помощью осциллографа. 8. Измерение частоты неизвестного сигнала по фигурам Лиссажу. 9. Найдите соотношение частот колебаний на рис. 9.
Рис. 9 (к заданию 9) 10. Электрон с некоторой начальной скоростью v 0 влетаетв плоский конденсатор параллельно пластинам на равном расстоянии от них. К пластинам конденсатора приложена разность потенциалов U = 300 В. Расстояние между пластинами d = 2 см, длина конденсатора l = 10 см. Какой должна быть предельная начальная скорость электрона, чтобы электрон не вылетел из конденсатора? 11. Электрон, пройдя ускоряющую разность потенциалов ∆φ, влетает в плоский воздушный конденсатор параллельно пластинам, длина которых l. На конденсатор подают напряжение, которое изменяется линейно со временем по закону U = α t, где α – положительная постоянная, t – время движения электрона в конденсаторе. Расстояние между пластинами конденсатора d. Определить, с какой скоростью электрон вылетит из конденсатора. 12. Узкий пучок электронов в вакууме пролетает сквозь плоский конденсатор параллельно его пластинам и попадает на флуоресцирующий экран, отстоящий от конденсатора на расстоянии L = 15 см. При подаче на конденсатор напряжения U =50 В светящееся пятно на экране смещается на s = 21 мм. Расстояние между пластинами конденсатора d = 18 мм; длина конденсатора l = 6 см. Определите начальную скорость электрона. 13. Электрон влетает в плоский горизонтальный конденсатор параллельно пластинам со скоростью 9·106 м/с. Найти полное, нормальное и тангенциальное ускорение электрона через 10-8 с после начала его движения в конденсаторе. Разность потенциалов между пластинами равна 100 В, расстояние между пластинами 1 см. 14. Электрон влетает в плоский горизонтальный конденсатор параллельно его пластинам со скоростью 1·107 м/с. Напряженность поля в конденсаторе E = 100 В/см, длина конденсатора l = 5 см. Найти величину и направление скорости электрона при вылете его из конденсатора. 15. Электрон, находящийся в однородном электрическом поле, получает ускорение, равное 1·104 см/с2. Найти: 1) напряженность электрического поля, 2) скорость, которую получит электрон за 10-8 с своего движения, 3) работу сил поля за это время, 4) разность потенциалов, пройденную при этом электроном в поле. Лабораторная работа № 2 ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ С ПОМОЩЬЮ ЭЛЕКТРОПРОВОДНОЙ БУМАГИ
Цель работы: изучение метода моделирования электростатического поля с помощью электропроводной бумаги. Приборы и принадлежности: планшет с электродами для крепления электропроводной бумаги, вольтметр, источник постоянного тока на модуле МО-З, масштабная линейка. Краткая теори я Электрические заряды создают вокруг себя поле, называемое электрическим. Напряженность электрического поля Е определяется как сила, действующая на единичный положительный заряд, помещенный в данную точку поля, т. е.
Потенциал электрического поля определяется как потенциальная энергия W п, которой обладал бы положительный заряд, помещенный в данную точку поля
Элементарная работа, совершаемая силами электрического поля равна
где dl - перемещение заряда под действием силы F, El - проекция вектора E на направление перемещения l. Эта работа равна убыли потенциальной энергии
Из выражения (2) приращение потенциальной энергии равно
Подставив (3) и (5) в (4) получим
Поскольку l - любое произвольно выбранное направление, то компоненты вектора Е в декартовых координатах будут:
Вектор Е в декартовых координатах
или
Выражение, стоящее в скобках в формуле (9), носит название градиента скалярной величины j и записывается сокращенно в виде
Так как градиент любой скалярной величины есть вектор, направленный в сторону наиболее быстрого возрастания этой величины, то из соотношения (10) видно, что вектор Е направлен в сторону наиболее быстрого убывания потенциала. Если это направление обозначить r, то
Для однородного электрического поля (Е = const) можно написать
где ∆φ - разность потенциалов между двумя точками электри- ческого поля, находящимися на расстоянии ∆r друг от друга.
Порядок выполнения работы Задание 1. Исследование поля плоского конденсатора.
На Рис. 1а изображена электрическая схема установки, а на рис. 1б - установка для исследования электростатических полей (МО-3). 1 – электропроводная бумага, 2 – зонд, 3 – обкладки плоского конденсатора, 4 – обкладки цилиндрического конденсатора.
Рис. 1а Рис.1б 1. Закрепите электропроводную бумагу под электродами плоского и цилиндрического конденсаторов на планшете, обеспечивая хороший контакт по всей поверхности соприкосновения электродов с бумагой. 2. Соберите электрическую цепь по схеме, изображенной на рис.1а. После проверки схемы лаборантом или преподавателем подключите ее к источнику постоянного напряжения –9 + 9 В (клеммы источника расположены на планшете МО-З).
4. Перемещая зонд 2 по бумаге вдоль какого-либо из электродов 3, найдите точки с таким же потенциалом φ1 и проколите бумагу в этих точках на расстоянии 1 – 2 см друг от друга (рис.2). Через эти точки проведите эквипотенциальную линию. 5. Найдите и проколите острием зонда точки, соответствующие второй эквипотенциальной линии φ2, потенциал которой больше на 1,5 – 2 В. Рис. 2 (к п.4) 6. Повторите операции, аналогичные пунктам 3 – 5 еще для 5 – 7 эквипотенциальных линий. Обозначьте потенциалы всех эквипотенциальных линий на бумаге. Занесите значения потенциалов φ i всех линий в табл. 1. 7. Обведите контуры электродов на электропроводной бумаге, укажите их знаки (+ и -) и снимите бумагу с планшета. 8. Проведите линии равного потенциала и постройте систему силовых линий. Схема эквипотенциальных и силовых между электродами плоского конденсатора показана на рис. 2. 9. Вдоль центральной силовой линии измерьте расстояния ∆ xi от первой эквипотенциальной линии до каждой последующей (рис. 3). Данные занесите в табл. 1.
Рис. 3. Измерение ∆xi вдоль центральной силовой линии. 10. На миллиметровой бумаге нанесите экспериментальные точки зависимости ∆φ и ∆ x. Постройте график этой зависимости методом наименьших квадратов, используя формулу (13).
Эта формула выражает значение эквивалентной напряженности Е (В/м) однородного электрического поля. Таблица 1
Задание 2. Исследование поля цилиндрического конденсатора Соберите электрическую цепь по схеме на рис.4. Постройте линии равного потенциала и силовые линии для цилиндрического конденсатора аналогично тому, как это сделано для плоского конденсатора (пункты 2 - 8). Вдоль одной из силовых линий проведите измерения расстояний D r. Занесите результаты измерений в табл. 2. Постройте график зависимости ∆φ от ∆r (очевидно, что эта зависимость не будет линейной, так как в этом случае поле неоднородное).
Рис. 4. Электрическая схема для исследования поля цилиндрического конденсатора.
Таблица 2
Задания для отчета
1. Электрическое поле и его характеристики. Графическое изображение электрического поля. Силовые линии и эквипотенциальные поверхности. 2. Связь между напряженностью и потенциалом электрического поля. 3. Напряженность поля точечного заряда. Потенциал поля точечного заряда. 4. Принцип суперпозиции для напряженности и потенциала электрического поля. 5. Теорема Гаусса и ее применение для расчета напряженности электрического поля бесконечной равномерно заряженной плоскости, двух и более плоскостей; бесконечной равномерно заряженной нити, цилиндра; равномерно заряженной сферы, объемно заряженного шара. 6. Схема экспериментальной установки и порядок построения линий равного потенциала. 7. Метод наименьших квадратов для построения линейных экспериментальных зависимостей. 8. Три концентрические сферы радиусами R, 2 R, 3 R имеют за- ряды + q, +2 q, -3q соответственно. Определить потенциал каждой сферы. 9. Внутри полой тонкостенной проводящей сферы радиусом R находится другая концентрическая сфера радиусом r (r < R). Большой сфере сообщили за ряд Q, малой – заряд q. Определить потенциалы сфер. 10. Металлический заряженный шар радиусом R 1 помещен в центре проводящей сферической оболочки, внутренний и внешний радиусы которой соответственно равны R 2 и R3. Заряд шара Q. Напишите выражения и постройте график зависимости напряженности поля E и потенциала φ от расстояния r от центра шара.
Лабораторная работа № 3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 599; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.3.63 (0.007 с.) |


 (1)
(1) (2)
(2) (3)
(3)


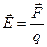 (1)
(1) (2)
(2) , (3)
, (3)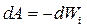 (4)
(4) . (5)
. (5) или (6)
или (6) . (7)
. (7)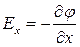 ,
,  ,
,  . (8)
. (8) ,
,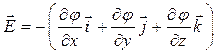 . (9)
. (9) . (10)
. (10) (11)
(11) , (12)
, (12)






 3. Выберите точку на бумаге вблизи отрицательного электрода на расстоянии приблизительно 0,5 - 1 см от него и с помощью зонда и вольтметра измерьте ее потенциал j 1, значение его занесите в табл. 1.
3. Выберите точку на бумаге вблизи отрицательного электрода на расстоянии приблизительно 0,5 - 1 см от него и с помощью зонда и вольтметра измерьте ее потенциал j 1, значение его занесите в табл. 1.

 . (13)
. (13)



