
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные реляционные операторыСодержание книги
Поиск на нашем сайте
Рассмотрим более подробно команды (операторы) РА. Автор реляционной модели данных (РМД) Ф. Кодд определил 8 основных операторов РА. 1. Селекция (WHERE) – выбор из таблицы-аргумента только тех записей, которые удовлетворяют заданному в операторе условию, например расписание группы 1030: РАСПИСАНИЕ WHERE НомерГруппы = '1030'; или в других обозначениях: s НомерГруппы = '1030' (РАСПИСАНИЕ). 2. Проекция ([ ]) – отбор из таблицы-аргумента только тех столбцов (полей), которые указаны в операторе, например номера групп, хранящихся в базе данных: ГРУППА [НомерГруппы]; или в других обозначениях: p НомерГруппы (ГРУППА). 3. Объединение(UNION) – слияние двух таблиц-аргументов в одну по вертикали, при этом к записям первой таблицы добавляются те записи из второй таблицы, которые отсутствуют в первой, например R UNION S, где R и S – некоторые таблицы, имеющие эквивалентные схемы; или в других обозначениях: R È S. 4. Разность(EXCEPT) – удаление из таблицы-уменьшаемого тех записей, которые принадлежат таблице-вычитаемому, например R EXCEPT S, где R и S – некоторые таблицы, имеющие эквивалентные схемы; или в других обозначениях: R ─ S. 5. Пересечение (INTERSECT) – удаление из первой таблицы-аргумента тех записей, которые не принадлежат второй таблице-аргументу, например R INTERSECT S, где R и S – некоторые таблицы, имеющие эквивалентные схемы; или в других обозначениях: R Ç S. Примеры операций È, ─ и Ç приведены в табл. 5. 6. Декартово произведение(TIMES) – слияние двух таблиц-аргументов в одну по горизонтали таким образом, что каждая запись первой таблицы соединяется по горизонтали с каждой записью второй таблицы (конкатенация строк). В таблице-результате заголовок будет равен объединению заголовков таблиц-аргументов, а тело – произведению мощностей таблиц-аргументов. Например, чтобы получить таблицу ЗАНЯТИЕ, содержащую все возможные варианты проведения занятий в течение недели вида: < Номер пары, НомерДня >, необходимо перемножить таблицы ДЕНЬ и ПАРА, т.е. ЗАНЯТИЕ = ДЕНЬ TIMES ПАРА; или в других обозначениях: ДЕНЬ ⊗ ПАРА. Результат выполнения этой операции приведен в табл. 6. Таблица 5
Таблица 6
7. Соединение(JOIN) - слияние двух таблиц-аргументов в одну по горизонтали таким образом, что каждая запись первой таблицы соединяется по горизонтали с каждой записью второй таблицы (конкатенация строк), но только в том случае, когда значения одноименных полей обеих таблиц равны. В таблице-результате заголовок будет равен объединению заголовков таблиц-аргументов за исключением полей второй таблицы совпадающих с соответствующими полями первой, а тело будет равно произведению мощностей таблиц-аргументов за исключением не соединившихся записей. Например, чтобы получить полное расписание занятий для какой-либо группы с указанием аудитории, времени начала, дисциплины преподавателя и вида занятий, требуется соединить соответствующие таблицы, т.е. РАСПИСАНИЕ_ГР_1030 = (((((((((РАСПИСАНИЕ JOIN ЗАНЯТИЕ) JOIN ПАРА) JOIN АУДИТОРИЯ) JOIN ПРЕПОДАВАТЕЛЬ) JOIN ДИСЦИПЛИНА) JOIN ВИДЗАН) JOIN ДЕНЬ) WHERE НомерГруппы = '1030') [НазваниеДня, ВремяНачала, НазваниеДисц, ИмяПреподав, НазваниеВидаЗан, НомерАуд]). В этом запросе, кроме операции соединения, использованы также операции селекции и проекции. Или в других обозначениях: π НазваниеДня, ВремяНачала, НазваниеДисциплины, ИмяПреподавателя, НазваниеВидаЗан, НомерАуд (σ НомерГруппы='1030' (((((РАСПИСАНИЕ «ЗАНЯТИЕ) «ПАРА) «АУДИТОРИЯ) «ПРЕПОДАВАТЕЛЬ) «ДИСЦИПЛИНА)). 8. Деление(DIVISION) – операция, в которой таблица-делитель должна иметь поля, входящие во множество полей таблицы-делимого. Если представить их схемы в обобщенном виде как R (A, B) и S (B), то S Пн, 1 Вт, 2 Ср, 3 Искомый запрос будет выглядеть следующим образом: ПРЕПОД_1_2_3 (ИмяПрепод) =(((((РАСПИСАНИЕ JOIN ПРЕПОДАВАТЕЛЬ) JOIN ЗАНЯТИЕ) JOIN ДЕНЬ)[ИмяПрепод, НазваниеДня, НомерПары]) DIVISION ПН1_ВТ2_СР3. В этом примере требуется сначала соединить таблицы, в которых размещаются нужные нам поля, затем выполнить над результатом соединения операцию проекции и в заключение разделить эту проекцию на вспомогательную таблицу. Или в других обозначениях: (((РАСПИСАНИЕ «ПРЕПОДАВАТЕЛЬ) «ЗАНЯТИЕ) «ДЕНЬ) ¸ ПН1_ВТ2_СР3. Из восьми вышеперечисленных реляционных операций пять операций образуют минимальную алгебру Кодда, к ним относятся операции Селекция, Проекция, Разность, Объединение и Декартово произведение. Оставшиеся три операции могут быть выражены через эти пять. Например, Пересечение: R INTERSECT S = R EXCEPT (R EXCEPT S) или R Ç S = R – (R – S). Соединение: R JOIN S = ((R(A, B, C) TIMES S(C, D, E)) WHERE R.C=S.C) [A, B, R.C, D, E] или R. « S = s R.C=S.C (R Ä S). Деление: R(A, B, C) DIVISION S(C) = R[A, B] EXCEPT ((R[A, B] TIMES S) EXCEPT R) [A, B] или R(A, B, C) ¸ S(C) = p A, B (R) –p A, B ((p A, B (R) Ä S) – R).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.174 (0.006 с.) |

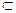 R. Заголовок таблицы-частного будет равен разности R-S, а тело образуют те записи таблицы-делимого, которые соединятся с каждой записью таблицы-делителя. Например, чтобы определить, кто из преподавателей проводит занятия в понедельник первой парой, во вторник – второй парой, а в среду – третьей парой, необходимо разделить таблицу РАСПИСАНИЕ на специально сконструированную таблицу, к примеру ПН1_ВТ2_СР3 (НазваниеДня, НомерПары)
R. Заголовок таблицы-частного будет равен разности R-S, а тело образуют те записи таблицы-делимого, которые соединятся с каждой записью таблицы-делителя. Например, чтобы определить, кто из преподавателей проводит занятия в понедельник первой парой, во вторник – второй парой, а в среду – третьей парой, необходимо разделить таблицу РАСПИСАНИЕ на специально сконструированную таблицу, к примеру ПН1_ВТ2_СР3 (НазваниеДня, НомерПары)


