
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения прямой на плоскости.Содержание книги
Поиск на нашем сайте Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнений. Уравнение прямой с угловым коэффициентом. Пусть на плоскости Оху задана произвольная прямая, не параллельная оси Оу. Ее положение вполне определяется ординатой b точки N (0; b) пересечения с осью Оу и углом α между осью Ох и прямой (рис. 13). Под углом α (0 ≤ α < π) наклона прямой понимается наименьший угол, на который нужно повернуть против часовой стрелки ось Ох до ее совпадения с прямой.
Рис. 13 Из определения тангенса угла следует равенство т. е.
Число Если прямая проходит через начало координат, то b = 0 и, следовательно, уравнение этой прямой будет иметь вид Если прямая параллельна оси Ох, то α = 0, следовательно, Если прямая параллельна оси Оу, то
где а — абсцисса точки пересечения прямой с осью Ох. Отметим, что уравнения (4) и (5) есть уравнения первой степени. Общее уравнение прямой. Рассмотрим уравнение первой степени относительно х и у в общем виде
где А, В, С — произвольные числа, причем А и В не равны нулю одновременно. Уравнение (6) есть уравнение прямой линии, оно называется общим уравнением прямой. Вектор n={A,B} называется вектором нормали к прямой, он перпендикулярен прямой (6). Некоторые частные случаи общего уравнения прямой: 1) если А = 0, то уравнение приводится к виду 2) если В = 0, то прямая параллельна оси Оу; 3) если С = 0, то получаем
Условия параллельности, перпендикулярности двух прямых Пусть даны 2 прямые общими уравнениями:
Если
Если
Угол между прямыми
|
||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |


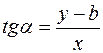 ,
, . Введем обозначение
. Введем обозначение 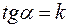 , получаем уравнение
, получаем уравнение . (4)
. (4) называется угловым коэффициентом прямой, а уравнение (4) — уравнением прямой с угловым коэффициентом.
называется угловым коэффициентом прямой, а уравнение (4) — уравнением прямой с угловым коэффициентом. .
. и уравнение (4) примет вид у = b.
и уравнение (4) примет вид у = b. , уравнение (4) теряет смысл, т. к. для нее угловой коэффициент
, уравнение (4) теряет смысл, т. к. для нее угловой коэффициент  не существует. В этом случае уравнение прямой будет иметь вид
не существует. В этом случае уравнение прямой будет иметь вид , (5)
, (5) , (6)
, (6) . Это есть уравнение прямой, параллельной оси Ох;
. Это есть уравнение прямой, параллельной оси Ох; . Уравнению удовлетворяют координаты точки О(0; 0), прямая проходит через начало координат.
. Уравнению удовлетворяют координаты точки О(0; 0), прямая проходит через начало координат. и
и
 ||
||  , то векторы нормалей
, то векторы нормалей  и
и  коллинеарны, тогда их координаты пропорциональны, следовательно,
коллинеарны, тогда их координаты пропорциональны, следовательно, - условие параллельности прямых.
- условие параллельности прямых.
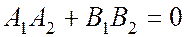 - условие перпендикулярности прямых.
- условие перпендикулярности прямых. - формула для нахождения угла между прямыми.
- формула для нахождения угла между прямыми.


