
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: аналитическая геометрия на плоскостиСтр 1 из 2Следующая ⇒
Тема: АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ Л е к ц и я 5 СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ. УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ Основные понятия. Основные приложения метода координат на плоскости. Линии на плоскости. Уравнения прямой на плоскости. Прямая на плоскости. Основные задачи. Основные понятия. Прямоугольную систему координат обозначают Рассмотрим произвольную точку М плоскости
Координатами точки М в системе координат Эти два числа х и у полностью определяют положение точки на плоскости, а именно: каждой паре чисел х и у соответствует единственная точка М плоскости, и наоборот. Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой О, называемой полюсом, лучом Ор, называемым полярной осью, и единичным вектором Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием Рис. 1 стрелки) (рис. 1).
Числа r и φ называются полярными координатами точки М, пишут Для получения всех точек плоскости достаточно полярный угол φ ограничить промежутком Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс О с началом координат системы Из рисунка 2 видно, что прямоугольные координаты точки М выражаются через полярные координаты точки следующим образом:
Определяя величину φ, следует установить (по знакам х и у) четверть, в которой лежит искомый угол, и учитывать, что Основные приложения метода координат на плоскости. Линии на плоскости. Линия на плоскости рассматривается (задается) как множество точек, обладающих некоторым только им присущим геометрическим свойством. Например, окружность радиуса R есть множество всех точек плоскости, удаленных на расстояние R от некоторой фиксированной точки О (центра окружности). Уравнением линии (или кривой) на плоскости Оху называется такое уравнение F(x;y) = 0 с двумя переменными, которому удовлетворяют координаты х и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. Переменные х и у в уравнении линии называются текущими координатами точек линии. Уравнение линии позволяет изучение геометрических свойств линии заменить исследованием его уравнения. Так, для того чтобы установить, лежит ли точка А(хо;уо) на данной линии, достаточно проверить (не прибегая к геометрическим построениям), удовлетворяют ли координаты точки А уравнению этой линии в выбранной системе координат. Задача о нахождении точек пересечения двух линий, заданных уравнениями F1(x;y) = 0 и F2(x;y) = 0, сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, т. е. сводится к решению системы двух уравнений с двумя неизвестными:
F1 (x; y) = 0, F2 (x; y) = 0. Если эта система не имеет действительных решений, то линии не пересекаются. Аналогичным образом вводится понятие уравнения линии в полярной системе координат. Уравнение F (r; φ) = 0 называется уравнением данной линии в полярной системе координат, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.
x = x (t), y = y (t), (3) где х и у — координаты произвольной точки М (х; у), лежащей на данной линии, a t — переменная, называемая параметром; параметр t определяет положение точки (x; у) на плоскости.
Например, если x = t + 1, y = t2, то значению параметра t = 2 соответствует на плоскости точка (3; 4), т. к. х = 2 + 1 = 3, у = 22 = 4. Если параметр t изменяется, то точка на плоскости перемещается, описывая данную линию. Такой способ задания линии называется паpaметрическим, а уравнения (3) — параметрическими уравнениями линии. В аналитической геометрии на плоскости возникают две основные задачи. Первая: зная геометрические свойства кривой, найти ее уравнение; вторая: зная уравнение кривой, изучить ее форму и свойства.
Общее уравнение прямой. Рассмотрим уравнение первой степени относительно х и у в общем виде
где А, В, С — произвольные числа, причем А и В не равны нулю одновременно. Уравнение (6) есть уравнение прямой линии, оно называется общим уравнением прямой. Вектор n={A,B} называется вектором нормали к прямой, он перпендикулярен прямой (6). Некоторые частные случаи общего уравнения прямой: 1) если А = 0, то уравнение приводится к виду 2) если В = 0, то прямая параллельна оси Оу; 3) если С = 0, то получаем
Тема: АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ Л е к ц и я 5 СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 467; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.251.22 (0.015 с.) |
 , а плоскость, в которой расположена система координат, называют координатной плоскостью.
, а плоскость, в которой расположена система координат, называют координатной плоскостью. называется радиусом-вектором точки М.
называется радиусом-вектором точки М.
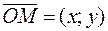 , то координаты точки М записывают так: М(х;у), число х называется абсциссой точки М, у — ординатой точки М.
, то координаты точки М записывают так: М(х;у), число х называется абсциссой точки М, у — ординатой точки М. того же направления, что и луч Ор.
того же направления, что и луч Ор. от полюса О и
от полюса О и  углом φ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой
углом φ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой , при этом r называют полярным радиусом, φ — полярным углом.
, при этом r называют полярным радиусом, φ — полярным углом. (или
(или  ), а полярный радиус —
), а полярный радиус —  . В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, иобратно.
. В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, иобратно. . Рис 2.
. Рис 2.

 ,
,
 .
Полярные же координаты точки М выражаются через декартовы координаты (тот же рисунок) такими формулами:
.
Полярные же координаты точки М выражаются через декартовы координаты (тот же рисунок) такими формулами:

 ,
, .
. .
.
 Линию на плоскости можно задать при помощи двух уравнений:
Линию на плоскости можно задать при помощи двух уравнений: На рисунках 4-12 приведены примеры некоторых кривых и указаны их уравнения.
На рисунках 4-12 приведены примеры некоторых кривых и указаны их уравнения.






 ,
,  ;
в полярных координатах:
;
в полярных координатах:
 .
.
 , где a > 0.
, где a > 0.



 .
.


 или
или


 .
.
 j
параметрические уравнения:
j
параметрические уравнения:


 , где а > 0. Кардиоида — частный случай улитки Паскаля (а = b).
, где а > 0. Кардиоида — частный случай улитки Паскаля (а = b).
 , где а > 0 — постоянное.
, где а > 0 — постоянное.



 , (6)
, (6) . Это есть уравнение прямой, параллельной оси Ох;
. Это есть уравнение прямой, параллельной оси Ох; . Уравнению удовлетворяют координаты точки О(0; 0), прямая проходит через начало координат.
. Уравнению удовлетворяют координаты точки О(0; 0), прямая проходит через начало координат.


