
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С. В. Засорин, Н. Г. Кипарисова, В. Г. СаламатинСодержание книги
Поиск на нашем сайте МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ РЯЗАНСКИЙ ИНСТИТУТ (филиал) Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ» С.В.Засорин, Н.Г.Кипарисова, В.Г.Саламатин ИНФОРМАТИКА Руководство по проведению лабораторных работ Основы работы в MATHCAD Рязань 2011 УДК 681.32 ББК
Засорин С.В., Кипарисова Н.Г., Саламатин В.Г.
Информатика. Руководство по проведению лабораторных работ. Основы работы в MATHCAD. Рязань: РИ(ф) МГОУ, 2011. – 54 с.
Рецензент: к.т.н., доцент Оборина Т.А.
В настоящих Методических указаниях приводятся описания трёх лабораторных работ по дисциплине «Информатика», которые выполняются студентами первых курсов очной формы обучения. Целью лабораторного практикума является получение студентами практических навыков применения возможностей MATHCAD при решении инженерных и экономических задач. Все описания ориентированы на использование MATHCAD 2001(версия 10)- MATHCAD 12. Методические указания содержат теоретическую часть, в которой рассматриваются возможности MATHCAD. В практической части содержатся описания последовательности решения задач на конкретных примерах, а также несколько практических заданий для самостоятельного выполнения студентами и контрольные вопросы. Методические указания предназначены для студентов специальности 080100, 080200, 151900, 270800, 271101 всех форм обучения.
Печатается по решению методического совета Рязанского института (филиала) Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Московский Государственный открытый университет». © Рязанский институт (филиал) Федерального государст- венного бюджетного образовательного учреждения высшего профессионального образования «Московский государственный открытый университет», 2011
© Засорин С.В., Кипарисова Н.Г., Саламатин В.Г., 2011
Содержание Введение ………………………………………………………………..3 Лабораторная работа №1. Основы сведения о среде Mathcad. Элементарные вычисления, графики ………………………………………..4 Лабораторная работа № 2. Векторы и матрицы в Mathcad. Решение систем линейных алгебраических уравнений………………………………26 Лабораторная работа № 3. Решение в среде Mathcad нелинейных алгебраических и трансцендентных уравнений и систем уравнений. Дополнительные возможности Mathcad …………………………………………..41 Литература……………………………………………………………..53
Введение
Mathcad -один из самых популярных математических пакетов, который позволяет производить различные вычисления с использованием принятых в математике обозначений. Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT), соучредителем компании Mathsoft, которая с 2006 года является частью корпорации PTC (Parametric Technology Cоrporation). С помощью Mathcad можно в символьном и численном виде: - выполнять простейшие расчеты по формулам, используя пакет как инженерный калькулятор; - решать нелинейные уравнения и системы; - решать задачи линейной алгебры; - обрабатывать экспериментальные данные (путем интерполяции и аппроксимации методом наименьших квадратов); - дифференцировать и интегрировать; - решать задачи оптимизации, в том числе задачи математического программирования; - решать задачи математической статистики и теории вероятностей; - проводить финансовые расчеты; - решать обыкновенные дифференциальные уравнения и системы; - решать дифференциальные уравнения в частных производных. Кроме того, Mathcad предоставляет широкие возможности для создания и редактирования различных графиков. Пакет математических вычислений Mathcad позволяет обмениваться данными с другими приложениями: Excel, Matlab, Axum и др. Mathcad является идеальным инструментом для выполнения инженерных и математических расчетов. Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в крупных инженерных проектах. Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчётов. Первый выпуск Mathcad был осуществлён в 1986 году. 7 июня 2010 года вышла очередная, пятнадцатая, версия пакета. Почти каждая версия приносит новые возможности.
Порядок выполнения работы 1. Изучите теоретический материал. Выполните в MathCAD решение всех примеров, встречающихся в тексте. 2. Выполните задание в соответствии с вашим вариантом. Номер варианта дается преподавателем. 3. Сформулируйте выводы по работе и ответьте на контрольные вопросы. Содержание отчета 1. Титульный лист. 2. Цель работы. 3. Результаты выполнения практического задания. 4. Выводы по работе. МЕНЮ MATHCAD Большинство вычислений в Mathcad можно выполнить тремя способами: - выбором операции в меню; - с помощью кнопочных панелей инструментов; - обращением к соответствующим функциям. Основные операции, закрепленные за пунктами меню, дублируются соответствующими кнопками панелей инструментов. Во всех трех случаях соблюдается один и тот же порядок действий: - выбор операции производится щелчком мыши по пункту меню или по кнопке в панели инструментов, после чего, если нужно, пользователь получает доступ к ниспадающему меню или к дополнительной панели; - когда операция выбрана, пользователь вводит необходимую информацию в окне диалога или заполняет помеченные поля в поле ввода, которое открывается непосредственно в рабочем документе.
Рисунок 1.1.1 - Окно программы Mathcad
Верхняя строка окна – стандартная строка windows-приложений. Она содержит имя приложения, имя файла, в котором сохраняются результаты. Справа располагаются три стандартные кнопки для работы с окнами Windows, позволяющие свернуть, развернуть на полный экран и закрыть окно приложения. Вторая строка рабочего окна Mathcad - строка меню. Меню имеет набор стандартных для windows-приложений пунктов, например, File(Файл), Edit(Редактировать), View(Просмотр) и т.п. Кроме того, здесь же располагаются специфические для Mathcad пункты, например, Insert(Вставка), Symbolic(Символьные операции) и т.п. Щелчок по пункту меню открывает ниспадающее меню со списком доступных в данном пункте операций. Некоторые строки ниспадающих меню содержат знак В окне Mathcad обычно располагаются инструментов, часть из которых - стандартные для windows-приложений операции работы с файлами и текстами, а другая часть – специфические функции Mathcad, например, кнопка с надписью f(x) открывает список встроенных функций. В отдельной строке обычно располагается панель инструментов для выполнения математических операций Math Palette (Математическая палитра), каждая кнопка которой открывает дополнительную панель, содержащую кнопки операций с математическими объектами определенного класса (Рисунок 1.1.2).
Рисунок 1.1.2 – Математическая палитра
Правила работы со всеми панелями одинаковы: щелчком по кнопке открываем вспомогательную панель, щелчком по кнопке выбираем в ней нужную операцию и заполняем в рабочем документе помеченные позиции для ввода данных, аргументов или параметров операции. Панель Math Palette. Это панель математических инструментов (дословно "математическая палитра") - наиболее часто используемая панель, поскольку именно здесь расположены кнопки вычислительных операций и операций конструирования вычислительных процедур. Панель математических инструментов содержит восемь кнопок, каждая из которых открывает дополнительную панель математических операций. Далее, в каждой лабораторной работе будут описаны операции, используемые при решении задач. Здесь же просто перечислены кнопки панели математических операций и приведен вид каждой дополнительной панели. Кнопка Щелчком по кнопке этой панели в рабочий документ вставляем имя функции, символ, цифру или знак операции с помеченными для ввода позициями. Кнопка
Кнопка
Кнопка Кнопка
Кнопка Кнопка Кнопка Видно, что кнопки панели дублируют соответствующие пункты меню символьных операций. Под строками панелей инструментов находится окно рабочего документа Mathcad – пространство, в котором располагаются все введённые команды и выражения, куда Mathcad выводит результаты вычислений и графики и где размещаются текстовые комментарии. Окно снабжено двумя полосами прокрутки – вертикальной и горизонтальной, что позволяет просматривать фрагменты окна, находящиеся вне пределов экрана.
Нижняя строка окна – строка состояния. В ней записаны рекомендации к дальнейшим действиям, описано текущее состояние среды и указан номер отображённой на экране страницы документа.
букв ключевых слов Работа с файлами и окнами Документы Mathcad хранятся в файлах с расширением.mcd.Чтобыоткрыть ранее сохраненный рабочий документ, выберите пункт Open из меню File. Mathcad запросит имя файла в диалоговом окне. Можно также использовать для этой цели "горячую" клавишу [F5]. Для сохранения рабочих документов Mathcad предоставляет двекоманды меню File: Save ("горячая" клавиша [F6]) и Save As. Последняяиспользуется для записи файла под другим именем, при сохранении неизменною его старой версии. При вызове этой команды появится диалоговое окно, в котором необходимо ввести новое имя файла. Для сохранения нового документа, никогда ранее не сохранявшегося, можно использовать любую из команд, в результате обеих появится новое диалоговое окно Save As. Для создания нового документа служит команда New меню File или клавиша [F7]. Для экспорта документа в текстовый процессор, например, MS Word, можно сохранить его в формате RTF (Rich Text Format). Окна Mathcad ведут себя подобно окнам других приложений Windows. Печать Чтобы напечатать весь рабочий документ Mathcad или его часть, используется пункт Print меню File, при выборе которого появится диалоговое окно, содержимое которого зависит от конкретного типа используемого принтера. Режим справки Mathcad предоставляет пользователю несколько удобных способовполучения справки. Щелчком по пункту Help (Помощь) в меню окна Mathcad открывается меню справочного режима. Пользователь, не имеющий навыков работы в среде Mathcad, может получить все необходимыеинструкции, обратившись к справочной системе.
Переменные и функции Для сохранения результатов промежуточных вычислений, а также для удобного манипулирования с исходными данными в MathCAD имеется возможность работы с переменными. Переменные MathCAD по своему назначению примерно соответствуют переменным алгоритмических языков программирования. Определение переменной задаёт значение переменной всюду ниже и правее места расположения определения. Чтобы в любой момент увидеть значение переменной, достаточно набрать её имя и символ «=». Для присвоения значения переменной используется оператор присваивания, который имеет следующий вид: имя переменной, знак присваивания – “:=”, выражение, значение которого присваивается переменной. В этом выражении могут содержаться числовые константы и ранее определённые переменные и функции. Слева от знака равенства могут стоять как имя простой переменной, так и имя переменной с верхними или нижними индексами, или матрица с элементами, являющимися простыми или индексированными переменными. Следует иметь в виду, что оператор присваивания вводится с клавиатуры нажатием клавиши <:>, а знак “равно” после двоеточия появляется автоматически. После того, как переменной было присвоено какое-либо значение, она может использоваться во всех формулах MathCAD. Если же попытаться использовать переменную, которой еще не присвоено значение, то это приведет к ошибке. Имена в Mathcad могут содержать любые из следующих символов: прописные и строчные латинские буквы; цифры от 0 до 9; знак подчёркивания «_»; штрих «`»; символ процента «%»; греческие буквы; символ бесконечности (∞). В Mathcad существует ряд ограничений на имена: - имя в Mathcad нельзя начинать с цифры, знака подчёркивания, штриха или символа процента; - Mathcad не делает различий между именами переменных и именами функций, то есть каждое из них должно быть уникальным; - символ бесконечности (∞) разрешается вводить только в качестве первого символа в имени; - Mathcad различает прописные и строчные буквы в именах, так ABC, ABc и abc – разные переменные. - символы, напечатанные после нажатия точки «.» будут записаны в нижнем индексе, но не надо путать эти буквенные нижние индексы, являющиеся частью имени переменной, с нижними индексами массивов; - некоторые имена употребляются для встроенных констант, переменных и функций (например, π, ∞, sin), и хотя никто не запрещает переопределить встроенные значения, следует помнить, что в этом случае встроенную функцию нельзя использовать в документе по первоначальному значению. Некоторые наиболее часто встречающиеся встроенные константы Mathcad показаны ниже: π – значение 3.1415926535897931 (число из 17 десятичных цифр, комбинация клавиш быстрого вызова Ctrl+Shift+p или Ctrl+G); e – значение 2.7182818284590451 (число из 17 десятичных цифр); ∞ - значение 10307 (бесконечность представляется максимальным числом в среде пакета, комбинация клавиш быстрого вызова Ctrl+Shift+z); TOL – значение 0.001 (величина ошибки при выполнении приближённых вычислений, она может быть переопеределена простым присваиванием); ORIGIN - значение 0 (нижняя граница индекса массива); % - значение 0.01 (используется для вычисления процента в величинах вида X*%). В Mathcad в переменных могут храниться строковые и числовые значения. Mathcad интерпретирует значения, начинающиеся цифрой, как числа. Используются следующие классы чисел: - вещественные (целые) числа; - комплексные числа – для ввода мнимого числа за его модулем надо поместить символ мнимой единицы i или j, но i или j нельзя применять сами по себе для ввода мнимых чисел, надо печатать 1i или 1j; - двоичные целые числа - их запись заканчивается строчной латинской буквой b, например 10101b; - восьмеричные целые числа - их запись заканчивается строчной латинской буквой o, например 756o; - шестнадцатеричные целые числа - их запись заканчивается строчной латинской буквой h, например 1a95h. В Mathcad Могут встретиться строки, строковые переменные и константы вводятся в двойных кавычках. Например, A:=” Green”. Первый символ в строке имеет номер 0. Mathcad различает в именах различные шрифты для переменных и функций пользователя. Имена, набранные различными шрифтами, являются разными. Имена встроенных переменных, функций и ключевые слова одинаково определены для всех шрифтов (кроме Symbol), размеров и стилей и могут быть набраны любым из них.
Пример 1.2 Вычислить значение выражения Щелкните мышью в любом месте листа вычислений. Для задания значения переменной
Рисунок 1.2.2 - Выполнение вычислений с использованием переменных
Еще одной широко используемой возможностью MathCAD является использование функций. Функции, используемые в Mathcad, разделяют на два класса: - встроенные; - определённые пользователем. Наиболее часто встречаются следующие математические функции: sin(x), cos(x) – вычисляет синус числа x и косинус числа x соответственно; tan(x), cot(x)) – вычисляет тангенс числа x и котангенс числа x соответственно; asin(x), acos(x)) – вычисляет арксинус числа x и арккосинус числа x соответственно; atan(x),acot(x)) – вычисляет арктангенс числа x и арккотангенс числа x соответственно; sinh(x), cosh(x)) – вычисляет гиперболический синус числа x и гиперболический косинус числа x соответственно; tanh(x), coth(x)) – вычисляет с гиперболический тангенс числа x и гиперболический котангенс числа x соответственно; exp(x)) – вычисляет ex; ln(x) – вычисляет натуральный логарифм числа x; log(x,a) – вычисляет логарифм числа x по основанию a; если a опущено, то вычисляется десятичный логарифм числа x. Mathcad позволяет определять функции как одного, так и нескольких аргументов. Для этого необходимо: - указать имя функции; - в круглых скобках перечислить через запятую аргументы функции; -набрать символ: и определить новую функцию. Имена из списка аргументов могут быть ещё не определены в рабочем документе. Аргументами функции могут быть скаляры, векторы и матрицы. При использовании функции в выражении Mathcad вычисляет значения аргументов, указанных в скобках, заменяет формальные параметры в определении функции фактическими значениями аргументов, выполняет действия, предписанные определением функции, и возвращает результат вычислений как значение функции. Если в определении функции используется имя переменной, которой нет в списке аргументов, то оно должно быть определено прежде определения функции. Значение этой переменной в момент определения функции становится её постоянной частью. Значение функции не будет зависеть от переопределения этой переменной в документе в дальнейшем. Использование функций во многом похоже на использование переменных, с той разницей, что у функции имеются один или несколько параметров. Для определения функции используется следующий оператор: имя функции, список параметров,:=, выражение, зависящее от параметров функции и определяющее ее значение. После определения значения функции, ее можно использовать так же, как любую встроенную функцию.
Пример 1.3 Определить функцию Щелкните Мышью в любом месте листа вычислений. Для определения функции введите с клавиатуры: <f>, <(>, <x>, <,> <y>, <)>, <:>, <e>, <^>, <x>, <пробел>, </>, <y>, <Enter>. Для вычисления значения функции введите с клавиатуры: <f>, <(>, <2>, <,>, <4>, <.>, <9>, <)>, <=>. Результат вычислений приведен на рисунке 1.2.3
Рисунок 1.2.3 - Определение и использование функций пользователя В математических задачах часто используются дискретные аргументы. Дискретные аргументы являются особым видом переменных. Дискретный аргумент последовательно принимает ряд значений, отделяемых одинаковыми шагами. Чтобы определить дискретный аргумент, надо ввести его имя, сопровождаемое двоеточием и диапазоном значений. При этом надо придерживаться следующих правил. 1. Для ввода диапазона значений, изменяющихся с шагом 1, надо ввести начальное и конечное значение, которые разделяются точкой с запятой «;», которая будет заменена системой на две точки. Пример n изменяется от 0 до 20 с шагом 1. Вводимые символы n:0;20 Вид в документе n:=0..20 2. Для ввода диапазона с произвольным шагом надо ввести начальное значение, запятую «,», второе значение, точку с запятой «;» и конечное значение. Пример k изменяется от -1 до 2 с шагом 0.1. Вводимые символы k:-1,-0.9;2 Вид в документе n:=-1,-0.9..2 ПРИМЕР 1.4 Определить функцию f(x) =
Построение графиков функций
MathCAD представляет собой мощное и удобное средство для построения графиков функций. Для построения графика функции одного аргумента необходимо выполнить следующее. 1. На панели инструментов “Графики” нажать кнопку “Декартов график” (кнопку с изображением двумерного графика 2. В поле ввода в левой части графика ввести имя функции с перечислением необходимых параметров. Если в одних и тех же координатах нужно построить несколько графиков, то указываются несколько функций, разделенных запятыми. 3. В поле ввода в нижней части графика ввести имя аргумента. 4. Нажмите <Enter> на клавиатуре или щелкните мышью вне графика. 5. При необходимости задается необходимый масштаб графика путем задания значений в полях ввода, расположенных у каждой из осей.
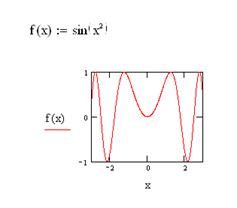
Пример 1.5 Построить график функции Введите функцию Нажмите кнопку
Рисунок 1.2.4 - Ввод имени функции в поле графика В поле ввода в нижней части графика введите <x>. Нажмите <Enter>. Результат ввода показан на рисунке 1.2.5
Рисунок 1.2.5 - Ввод названия аргумента в поле графика Щелкните мышью на изображении графика и в полях ввода внизу оси абсцисс введите – слева -3, а справа 3. Результат показан на рисунке 1.2.6
Рисунок 1.2.6 - Окончательное отображение графика При помощи команды трассировки Trace ( трассировка ) можно достаточно хорошо изучить строение графика. Вызывается эта команда из контекстного меню щелчком правой кнопки мыши (рисунок 1.2.7), из основного меню -(Format Для выполнения трассировки выделенного графика надо открыть диалоговое окно X-Y Trace, а затем, перемещая указатель мыши по графику, передвигать точку пересечения линий трассировки. На рисунке 1.2.8 показан пример подобных действий. Линии трассировки указывают на некоторую точку графика. При этом координаты точки отображаются в полях X-Value (Значение Х) и Y-Value (Значение Y) диалогового окна X-Y Trace. Кнопки Copy X и Copy Y предназначены для копирования значений абсциссы и ординаты исследуемой точки в буфер обмена и дальнейшей вставки в любое место документа. Выбор параметра Track data points (След точек данных) приведёт к тому, что линии трассировки будут следовать точно вдоль графика, иначе они перемещаются по всей графической области. (На рисунках 1.2.7 и 1.2.8 показано выполнение трассировки). Удобно изучать линии графика в увеличенном масштабе. Для этого в Mathcad существует диалоговое окно X-Y Zoom (Увеличить масштаб), которое выводится на экран только при выделенной графической посредством кнопки Для нанесения на график вспомогательных линий надо в области графика нажать правую кнопку мыши, выбрать Формат- ОсиХУ- Вспомогательные линии. Это повышает выразительность графика.
Рисунок 1.2.7 – Установка режима трассировки
Рисунок 1.2.8 – Определение координат выделенной точки графика
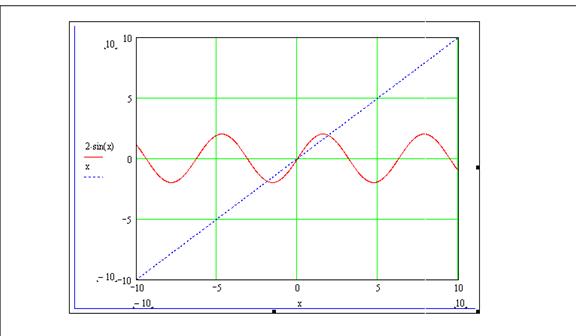
Для построения графиков нескольких функций в одних координатных осях необходимо при перечислении функций по оси ординат ставить запятую перед вводом следующего выражения только тогда, когда курсор полностью захватывает предыдущее. Пример 1.6 Построить графики функций 2sin(x), x. Результат показан на рисунке 1.2.9
Рисунок 1.2.9 – Построение графика нескольких функций в одних координатных осях
Пример 1. 7 Решите графически уравнение f(x) = 0, где f(x)=x3 +3x2 -2. На рисунке 1.2.10 приведён фрагмент рабочего документа Mathcad c соответствующими определениями, графиками и окнами диалога. Для решения задачи надо определить функцию f(x) и построить её график. Для того, чтобы найти корни уравнения – абсциссы точек пересечения графика с осью y = 0, надо щёлкнуть по строке Trace (Трассировка) контекстного меню. Затем надо щёлкнуть по полю графика и установить маркер в точке пересечения графика функции с осью абсцисс. В окне диалога отображаются координаты маркера: значение координаты x и есть искомое приближение. Результаты нахождения одного корня показаны на рисунке 1.2.10
Рисунок 1.2.10 – Пример нахождения приближённого значения корня уравнения
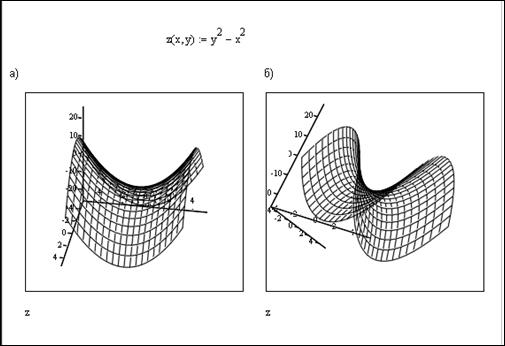
Пакет Mathcad обладает возможностями построения трёхмерных графиков различного типа. График поверхности (трёхмерный, или 3D-график) – это график, положение точки в котором определяется значениями трёх координат. Поверхности в Mathcad создаются быстро и просто. Пример 1.8 Построить график функции z(x, y) = y2 –x2. Выполним следующую последовательность действий. 1. Определим заданную функцию. 2. Вызовем шаблон для создания трёхмерного графика, нажав кнопку 3. Введём имя функции в шаблон построения графика. 4. Нажмём Enter или выйдем за пределы построения графика.
Рисунок 1.2.11 – Результаты выполнения Примера 1.8 Графики, показанные на рисунке 1.2.11 можно получить, выводя на экран шаблоны для построения поверхности в виде множества точек Функция в пространственной системе координат может также задаваться матрицей. Приведённые графики имеют достаточно примитивный вид. Отметим, что Mathcad обладает средствами для модификации уже созданной поверхности, например, возможен поворот (рисунок 1.2.12), перспектива, световые эффекты и т.д.
Рисунок 1.2.12 - Поворот графика Задания на практическую работу 1. Вычислите значение выражения: 1) 4)
2. Вычислите значение выражения 1) 2) 3) 4) 5) 3. Постройте график функции: 1) 4) 4. Решите графически уравнение: 1) cosx=0 в диапазоне x 2) x3-3x+x=0; 3) 4) x2+16/x-16=0; 5) 4-x-4/x2=0. 1.4 Контрольные вопросы 1. Возможности Mathcad. 2. Система меню Mathcad. 3. Панели инструментов Mathcad. 4. Работа с файлами и окнами в Mathcad. 5. Справочная система Mathcad. 6. Печать документов в Mathcad. 7. В каком порядке в MathCAD производится вычисление выражений? 8. Как в MathCAD производится ввод пользовательских функций? 9. Как в MathCAD осуществляется построение графика функции одной переменной? 10. Как в одних и тех же координатах построить графики нескольких функций?
Порядок выполнения работы 1. Изучите теоретический материал. Выполните в MathCAD решение всех примеров, встречающихся в тексте. 2. Выполните задание в соответствии с вашим вариантом. Номер варианта дается преподавателем. 3. Сформулируйте выводы по работе и ответьте на контрольные вопросы. Содержание отчета 1. Титульный лист. 2. Цель работы. 3. Результаты выполнения практического задания. 4. Выводы по работе. Функции сортировки sort(v) - сортирует элементы вектора v в порядке возрастания их значений. reverse(v) – переставляет элементы вектора v в обратном порядке. csort(A,n) – переставляет строки матрицы А таким образом, чтобы отсортировался n-й столбец. rsort(A,n) – переставляет столбцы матрицы А таким образом, чтобы отсортировалась n-я строка. Примеры, иллюстрирующие работу этих функций, приведены на рисунке 2.1.7 Выполняя операции над матрицами надо помнить их свойства, например, что суммировать можно только матрицы одинакового размера, а перемножать – лишь в том случае, если число столбцов первой матрицы равно числу строк второй.
Уравнений Рассмотрим пример символьного решения системылинейных алгебраических уравнений. Пример 2.6 Найти символьное решение системы линейных алгебраических уравнений, приведённой в примере 2.5 Для отыскания решения системы воспользуемся решающим блоком. Этот блок начинается ключевым словом Given, который следует набрать на клавиатуре. Уравнения системы записываются правее и ниже ключевого слова. Знак равенства в уравнениях вводится при помощи клавиш <Ctrl> + <=> или выбирается на панели инструментов Boolean (Логические операторы). Правее и ниже последнего уравнения системы вводится функция Find (x1, x2, …, xn). В скобках перечисляются имена переменных, значения которых надо найти. После ввода функции с и
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.119.128 (0.015 с.) |


 , означающий, что здесь доступны операции, список которых разворачивается, если приостановить курсор мыши на строке, помеченной значком
, означающий, что здесь доступны операции, список которых разворачивается, если приостановить курсор мыши на строке, помеченной значком 
 Arithmetic Palette (Калькулятор) открывает панель простейших вычислений (Рисунок 1.1. 3).
Arithmetic Palette (Калькулятор) открывает панель простейших вычислений (Рисунок 1.1. 3). - Evaluation and Boolean Palette (Панель равенств и отношений) открывает панель, изображенную на рисунке 1.1.4
- Evaluation and Boolean Palette (Панель равенств и отношений) открывает панель, изображенную на рисунке 1.1.4 Рисунок 1.1.3 -Панель калькулятора
Рисунок 1.1.3 -Панель калькулятора
 Рисунок 1.1.4 -Панельотношений
Рисунок 1.1.4 -Панельотношений
 Рисунок 1.1.5 - Панель графиков
Рисунок 1.1.5 - Панель графиков
 Graph Palette (Панель графиков) открывает панель, изображенную на рисунке 1.1.5
Graph Palette (Панель графиков) открывает панель, изображенную на рисунке 1.1.5 Vector and Matrix Palette (Панель векторных и матричных операций) открывает панель, изображенную на рисунке 1.1.6
Vector and Matrix Palette (Панель векторных и матричных операций) открывает панель, изображенную на рисунке 1.1.6 Calculus Palette (Панель операций математического анализа) открывает панель, изображенную на рисунке 1.1.7
Calculus Palette (Панель операций математического анализа) открывает панель, изображенную на рисунке 1.1.7 Рисунок 1.1.6 -Панель матричных операций
Рисунок 1.1.6 -Панель матричных операций
 Programming Palette (Панель программирования) открывает панель, представленную на рисунке 1.1.8
Programming Palette (Панель программирования) открывает панель, представленную на рисунке 1.1.8 Greek Symbol Palette (Панель греческих букв) открывает панель, изображенную на рисунке 1.1.9
Greek Symbol Palette (Панель греческих букв) открывает панель, изображенную на рисунке 1.1.9 Symbolic Keyword Palette (Ключевые слова символьных вычислений) открывает панель, изображенную на рисунке 1.1.10
Symbolic Keyword Palette (Ключевые слова символьных вычислений) открывает панель, изображенную на рисунке 1.1.10
 Рисунок 1.1.7- Панель операций Рисунок 1.1.8 - Панель программи-
математического анализа рования
Рисунок 1.1.7- Панель операций Рисунок 1.1.8 - Панель программи-
математического анализа рования
 Рисунок 1.1.9 -Панель греческих Рисунок 1.1.10 - Панель
Рисунок 1.1.9 -Панель греческих Рисунок 1.1.10 - Панель
 при
при  ,
,  .
. наберите на клавиатуре: <a>, <:>, <3>, <.>, <5>, <7>, <Enter>. Для задания значения переменной
наберите на клавиатуре: <a>, <:>, <3>, <.>, <5>, <7>, <Enter>. Для задания значения переменной  наберите на клавиатуре: <b>, <:>, <->, <5>, <.>, <2>, <Enter>. Для вычисления значения выражения наберите на клавиатуре: <a>, <^>, <2>, <пробел>, <+>, <2>, <*>, <a>, <*>, <b>, <=>. Результат вычислений представлен на рисунке 1.2.2
наберите на клавиатуре: <b>, <:>, <->, <5>, <.>, <2>, <Enter>. Для вычисления значения выражения наберите на клавиатуре: <a>, <^>, <2>, <пробел>, <+>, <2>, <*>, <a>, <*>, <b>, <=>. Результат вычислений представлен на рисунке 1.2.2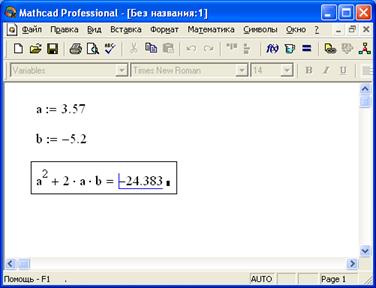
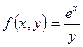 и вычислить ее значение при
и вычислить ее значение при 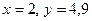 .
.
 , вычислить ее значение при х =1.2 и построить таблицу значений функции для х [0, 10] с шагом 1. В данном примере х является дискретным аргументом.
, вычислить ее значение при х =1.2 и построить таблицу значений функции для х [0, 10] с шагом 1. В данном примере х является дискретным аргументом.
 f(1.2)=.
Сразу после ввода знака равенства немедленно выводится вычисленное значение функции f(x) при х = 1.2.
f(1.2)=.
Сразу после ввода знака равенства немедленно выводится вычисленное значение функции f(x) при х = 1.2.



 ) или на клавиатуре нажать <Shift>+<2>.
) или на клавиатуре нажать <Shift>+<2>. на при
на при  .
.

 Graph
Graph  на панели инструментов Graph. После появления диалогового окна X-Y Zoom надо при помощи указателя мыши выбрать прямоугольную область на графике, а затем нажать кнопку, увеличения масштаба, выделенная область будет представлена в увеличенном масштабе. Кнопка обзора (Показать целиком) вернёт график в исходное состояние, а кнопка ОК оставит на графике только выделенную область в увеличенном виде.
на панели инструментов Graph. После появления диалогового окна X-Y Zoom надо при помощи указателя мыши выбрать прямоугольную область на графике, а затем нажать кнопку, увеличения масштаба, выделенная область будет представлена в увеличенном масштабе. Кнопка обзора (Показать целиком) вернёт график в исходное состояние, а кнопка ОК оставит на графике только выделенную область в увеличенном виде.


 на панели инструментов.
на панели инструментов.
 , гистограммы
, гистограммы  и линий поверхностей уровня или контурного графика
и линий поверхностей уровня или контурного графика  .
.
 ; 2)
; 2)  ; 3)
; 3) 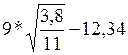 ;
; ; 5)
; 5) 
 при
при  ;
;  .
. при
при 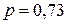 ;
;  .
. при
при 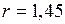 ;
;  .
. при
при  ;
;  .
. при
при  ;
;  .
. ; 2)
; 2)  ; 3)
; 3) 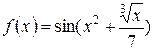 ;
; ; 5)
; 5)  .
. [0; 2];
[0; 2]; ;
;


