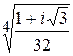Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найти пределы (не пользуясь правилом Лопиталя)Содержание книги
Поиск на нашем сайте
Вариант 1 1) Найти косинус угла между векторами
2) Коллинеарны ли векторы
3) Компланарны ли векторы
4) Вычислить площадь параллелограмма, построенного на векторах
5) Найти расстояние от точки
6) Написать уравнение плоскости, проходящей через точку
Вычислить.
9) Вычислить определитель 10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Найти пределы (не пользуясь правилом Лопиталя) а) в) д) 13) Найти производные
14) Найти а) у = х2ln x б) Найти производную указанного порядка.
Найти пределы пользуясь правилом Лопиталя а) Найти первые и вторые частные производные
Провести полное исследование функции и построить ее график.
Вариант 2 1) Найти косинус угла между векторами
2) Коллинеарны ли векторы
3) Компланарны ли векторы
4) Вычислить площадь параллелограмма, построенного на векторах
5) Найти расстояние от точки
6) Написать уравнение плоскости, проходящей через точку
Вычислить.
9) Вычислить определитель 10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Найти пределы (не пользуясь правилом Лопиталя) а) в) 13) Найти производные
14) Найти а) у = ех sin x б) Найти производную указанного порядка.
Найти пределы пользуясь правилом Лопиталя а) Найти первые и вторые частные производные
Провести полное исследование функции и построить их график.
Вариант 3 1) Найти косинус угла между векторами
2) Коллинеарны ли векторы
3) Компланарны ли векторы
4) Вычислить площадь параллелограмма, построенного на векторах
5) Найти расстояние от точки
6) Написать уравнение плоскости, проходящей через точку
Вычислить.
9) Вычислить определитель 10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Найти пределы (не пользуясь правилом Лопиталя) а) в) д) 13) Найти производные
14) Найти а) у = Найти производную указанного порядка.
Найти пределы пользуясь правилом Лопиталя а) Найти первые и вторые частные производные
Провести полное исследование функции и построить их график.
Вариант 4 1) Найти косинус угла между векторами
2) Коллинеарны ли векторы
3) Компланарны ли векторы
4) Вычислить площадь параллелограмма, построенного на векторах
5) Найти расстояние от точки
6) Написать уравнение плоскости, проходящей через точку
Вычислить.
9) Вычислить определитель 10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Вариант 5 1) Найти косинус угла между векторами
2) Коллинеарны ли векторы
3) Компланарны ли векторы
4) Вычислить площадь параллелограмма, построенного на векторах
5) Найти расстояние от точки
6) Написать уравнение плоскости, проходящей через точку
Вычислить.
9) Вычислить определитель 10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Вариант 6 1) Найти косинус угла между векторами
2) Коллинеарны ли векторы
3) Компланарны ли векторы
4) Вычислить площадь параллелограмма, построенного на векторах
5) Найти расстояние от точки
6) Написать уравнение плоскости, проходящей через точку
Вычислить.
9) Вычислить определитель 10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Вариант 7 1) Найти косинус угла между векторами
2) Коллинеарны ли векторы
3) Компланарны ли векторы
4) Вычислить площадь параллелограмма, построенного на векторах
5) Найти расстояние от точки
6) Написать уравнение плоскости, проходящей через точку
Вычислить.
9) Вычислить определитель 10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Вариант 8 1) Найти косинус угла между векторами
2) Коллинеарны ли векторы
3) Компланарны ли векторы
4) Вычислить площадь параллелограмма, построенного на векторах
5) Найти расстояние от точки
6) Написать уравнение плоскости, проходящей через точку
Вычислить.
9) Вычислить определитель 10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Вариант 9 1) Найти косинус угла между векторами
2) Коллинеарны ли векторы
3) Компланарны ли векторы
4) Вычислить площадь параллелограмма, построенного на векторах
5) Найти расстояние от точки
6) Написать уравнение плоскости, проходящей через точку
Вычислить.
9) Вычислить определитель 10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Вариант 10 1) Найти косинус угла между векторами
2) Коллинеарны ли векторы
3) Компланарны ли векторы
4) Вычислить площадь параллелограмма, построенного на векторах
5) Найти расстояние от точки
6) Написать уравнение плоскости, проходящей через точку
Вычислить.
9) Вычислить определитель 10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Вариант 1 1) Найти косинус угла между векторами
2) Коллинеарны ли векторы
3) Компланарны ли векторы
4) Вычислить площадь параллелограмма, построенного на векторах
5) Найти расстояние от точки
6) Написать уравнение плоскости, проходящей через точку
Вычислить.
9) Вычислить определитель 10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Найти пределы (не пользуясь правилом Лопиталя) а) в) д) 13) Найти производные
14) Найти а) у = х2ln x б)
|
||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 403; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.138.241 (0.011 с.) |

 и
и  .
.
 и
и  , построенные по векторам
, построенные по векторам  и
и  ?
?
 ?
?

 до плоскости, проходящей через точки
до плоскости, проходящей через точки  .
.
 перпендикулярно вектору
перпендикулярно вектору  .
.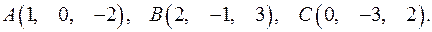

 где
где  ,
,  .
.


 б)
б) 
 г)
г) 

 данных функций:
данных функций:
 и
и 


 б)
б) 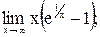









 ,
,  .
.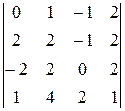

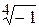
 б)
б) 
 г)
г)  ; д)
; д) 



 б)
б) 





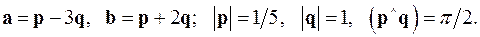


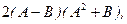
 ,
, 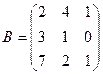 .
.


 б)
б) 
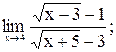 г)
г) 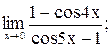


 б)
б) 

 б)
б) 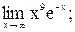









 ,
, 








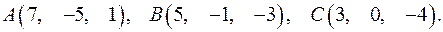

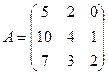 ,
,  .
.








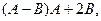
 ,
,  .
.



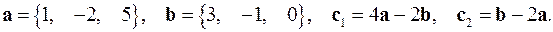


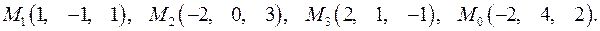


 ,
,  .
.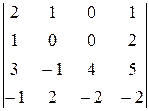








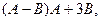
 ,
,  .
.


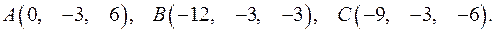





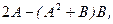
 ,
,  .
.

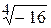







 ,
,  .
.