
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметри моделі парної лінійної регресії, їх сутність та оцінювання.Стр 1 из 8Следующая ⇒
Параметри моделі парної лінійної регресії, їх сутність та оцінювання. При розрахунках параметрів моделі лінійної регресії як правило застосовується метод найменших квадратів, але також можуть бути використані інші методи. Так само метод найменших квадратів може бути використаний і для нелінійних моделей. Тому МНК та лінійна регресія хоч і є тісно пов'язаними, але не є синонімами.Моделі лінійної регресії знайшли найбільш широке використання в економічних дослідженнях, хоча це і є спрощений засіб в моделюванні реальних економічних процесів. Якщо в рівняння включено лише одну пояснюючу змінну, то одержуємо теоретичну модель, яка дістала назву парної лінійної регресії: yі = β0 + β1xi + Теоретичну модель для парної лінійної регресії можна записати наступним чином: або у векторно-матричній формі, співвідношення буде мати такий вигляд:
Для визначення теоретичних коефіцієнтів β0, β1 необхідно буде використати всі значення (хі, уі) змінних Y і Х генеральної сукупності, що практично здійснити не можливо. Тому переходимо до побудови так званого емпіричного рівняння на базі інформації одержаної із вибірки. Емпіричне рівняння регресії має вигляд:
Перевірка суттєвості оцінок параметрів на основі t-критерію. Окрім загальних показників адекватності моделі існують також оцінки, що дають змогу встановити якість окремих частин рівняння, зокрема одного чи кількох коефіцієнтів регресії. Статистичну значущість кожного параметра моделі можна перевірити за допомогою t-критерію. При цьому нульова гіпотеза має вигляд Н0 : bj = 0, альтернативна НА : bj ≠ 0. Експериментальне значення t-статистики для кожного параметра моделі обчислюється за формулою
де Сjj – діагональний елемент матриці (Х′Х)–1;
Експериментальне значення tj-критерію порівнюється з табличним значенням tтабл з n–m–1 ступенями свободи при заданому рівні значущості a/2 (критична область розбивається на два фрагменти, межі яких задаються квантилем a/2). Якщо значення t-статистики потрапляє до критичної області (за абсолютним значенням перевищує tтабл), приймається альтернативна гіпотеза про значущість відповідного параметра. Інакше робиться висновок про статистичну незначущість параметра bj, а це означає, що відповідна незалежна змінна не впливає суттєво на змінювання залежної змінної.
Поняття фіктивних змінних. Серед економічних чинників, що розглядаються як пояснювальні змінні моделі, можуть бути й такі, які не можна виміряти кількісно, але вони істотно впливають на рівень зв’язку між залежною і пояснювальними змінними. Такі змінні дістали назву фіктивних змінних (dummy—змінних). Ці змінні можуть істотно розширити сферу застосування лінійних моделей, включивши їх до матриці пояснювальних змінних Х. Фіктивні зміни є певним чином сконструйованими змінними, що описують якісні показники, ознаки, а також відображають змінні в таких чинниках, як ефект зрушення в часі (сезонність) або змінюваність в просторі, або ж навіть включаються як змінна, що замінює інші пояснювальні змінні, яких раніше не було в моделі. Багато економетричних моделей попиту на різні товари можуть мати сезонні коливання, що необхідно враховувати через фіктивні змінні. Заробітна плата працюючих може імпульсивно змінюватись через зміну політичної влади, що спостерігалось в Україні. Ці коливання також можна врахувати, включивши до моделі фіктивні змінні. Алгоритм теста Глейсера. Глейзер. розглядає регресію модуля залишків 1) 3) У цих рівняннях Рішення про відсутність гетероскедастичності залишків приймається на підставі статистичної значущості коефіцієнтів Можливі чотири випадки: 1) 2) 3) 4) У першому випадку залишки гетероскедастичні, причому існує чиста і мішана гетероскедастичність. У другому випадку залишки мають мішану гетероскедастичність. Третій випадок свідчить про наявність чистої гетероскедастичності. У четвертому випадку гетероскедастичність відсутня.
Метод Гоморі. алгоритм, запропонований Гоморі, для розв’язування повністю цілочислової задачі лінійного програмування, що ґрунтується на використанні симплексного методу і передбачає застосування досить простого способу побудови правильного відтинання. Нехай маємо задачу цілочислового програмування:
Допустимо,щопараметри Параметри моделі парної лінійної регресії, їх сутність та оцінювання. При розрахунках параметрів моделі лінійної регресії як правило застосовується метод найменших квадратів, але також можуть бути використані інші методи. Так само метод найменших квадратів може бути використаний і для нелінійних моделей. Тому МНК та лінійна регресія хоч і є тісно пов'язаними, але не є синонімами.Моделі лінійної регресії знайшли найбільш широке використання в економічних дослідженнях, хоча це і є спрощений засіб в моделюванні реальних економічних процесів. Якщо в рівняння включено лише одну пояснюючу змінну, то одержуємо теоретичну модель, яка дістала назву парної лінійної регресії: yі = β0 + β1xi + Теоретичну модель для парної лінійної регресії можна записати наступним чином: або у векторно-матричній формі, співвідношення буде мати такий вигляд:
Для визначення теоретичних коефіцієнтів β0, β1 необхідно буде використати всі значення (хі, уі) змінних Y і Х генеральної сукупності, що практично здійснити не можливо. Тому переходимо до побудови так званого емпіричного рівняння на базі інформації одержаної із вибірки. Емпіричне рівняння регресії має вигляд:
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.96.159 (0.011 с.) |
 i
i
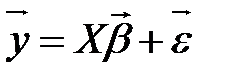 де:
де:






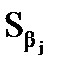 – стандартна похибка оцінки параметра моделі:
– стандартна похибка оцінки параметра моделі: , що відповідають регресії найменших квадратів, як певну функцію від
, що відповідають регресії найменших квадратів, як певну функцію від  , де
, де  . Для цього використовуються такі види функцій:
. Для цього використовуються такі види функцій: ; 2)
; 2) 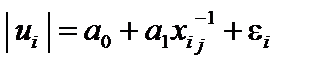 ;
; 4)
4)  .
.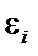 — стохастична складова.
— стохастична складова.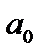 і
і 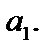 Переваги цього тесту визначаються можливістю розрізняти випадок чистої і мішаної гетероскедастичності.
Переваги цього тесту визначаються можливістю розрізняти випадок чистої і мішаної гетероскедастичності. є статистично значущими;
є статистично значущими; — статистично значуща,
— статистично значуща, 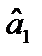 — статистично незначуща оцінка;
— статистично незначуща оцінка; за умов:
за умов:  ,
,  (8.6)
(8.6) ,
,  (8.7)
(8.7)  – цілі числа
– цілі числа  . (8.8)
. (8.8) – цілі числа. доведено, що за певних умов алгоритм Гоморі є скінченним, але процес розв’язування задач великої розмірності методом Гоморі повільно збіжний. Слід також мати на увазі, що і кількість ітерацій суттєво залежить від сформованого правильного відтинання. снують ефективніші відтинання, які використовуються у другому та третьому алгоритмах Гоморі, однак наявний практичний досвід ще не дає змоги виділити з них найкращий. Загалом, алгоритм Гоморі в обчислювальному аспекті є мало вивченим. Якщо в лінійному програмуванні спостерігається відносно жорстка залежність між кількістю обмежень задачі та кількістю ітерацій, що необхідна для її розв’язування, то для цілочислових задач такої залежності не існує. Кількість змінних також мало впливає на трудомісткість обчислень.
– цілі числа. доведено, що за певних умов алгоритм Гоморі є скінченним, але процес розв’язування задач великої розмірності методом Гоморі повільно збіжний. Слід також мати на увазі, що і кількість ітерацій суттєво залежить від сформованого правильного відтинання. снують ефективніші відтинання, які використовуються у другому та третьому алгоритмах Гоморі, однак наявний практичний досвід ще не дає змоги виділити з них найкращий. Загалом, алгоритм Гоморі в обчислювальному аспекті є мало вивченим. Якщо в лінійному програмуванні спостерігається відносно жорстка залежність між кількістю обмежень задачі та кількістю ітерацій, що необхідна для її розв’язування, то для цілочислових задач такої залежності не існує. Кількість змінних також мало впливає на трудомісткість обчислень.


