
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Элементы комбинаторикиСодержание книги
Поиск на нашем сайте
Число размещений, перестановок и сочетаний, число разбиений на множества заданной мощности.
Раздел 2. Булевые функции Тема 3. Булевые переменные и функции Булевые переменные и функции. Операции булевой алгебры. Задание булевых функций формулами и с помощью таблицы истинности. Эквивалентные формулы, основные эквивалентности. Тема 4. Дизъюнктивная и конъюнктивная нормальные формы Дизъюнктивная и конъюнктивная нормальные формы (ДНФ, КНФ) формул и их построение. Совершенные ДНФ, КНФ. Минимизация ДНФ, КНФ. Полиномиальное разложение: СПНФ, канонический полином Жегалкина, арифметический полином. Раздел 3. Основы теории алгоритмов Тема 5. Понятие алгоритма и сложность алгоритма Понятие алгоритма и оценка сложности алгоритма. Эвристические алгоритмы. «Жадные» алгоритмы. Раздел 4. Теория графов Тема 6. Основные понятия теории графов Граф как абстрактное математическое понятие. Вершины, рёбра, дуги. Понятие инцидентности. Способы задания графов. Матрицы графов и их свойства. Степени вершин графа. Теорема о вычислении вершин нечётной степени в графе (лемма о рукопожатиях). Тема 7. Виды графов, операции над ними Простой граф, мультиграф, псевдограф. Неориентированный и ориентированный графы (орграфы). Полный граф, звёздный граф и т.д. Двудольный граф, критерий двудольности. Понятие изоморфности графов. Инварианты. Части графа. Подграфы. Дополнение графа. Реберный граф. Основные операции над графами. Тема 8. Пути в графах, связность Пути в графах. Меры графов (эксцентриситет, диаметр, радиус, сумма расстояний, центр и центр тяжести). Связность графов. Компоненты графов. Теорема Менгера. Тема 9. Деревья и их свойства Деревья и их свойства. Остовные (каркасные) деревья в графе, алгоритмы построения. Теорема Кирхгоффа о количестве всех остовных (каркасных) деревьев в графе. Тема 10. Подструктуры графов Подструктуры графов. Клика. Нахождение наибольшей клики с помощью «жадного» алгоритма. Независимое множество вершин. Паросочетания. Вершинные и реберные покрытия. Тема 11. Циклы в графах, обходы графов Циклы в графах. Базовые (фундаментальные) циклы в графах. Обходы графов: Эйлеров и Гамильтонов циклы в графе. Алгоритм Флери. Теоремы о существовании Эйлерова и Гамильтонова циклов в графе. Понятие «почти все» графы. Теоремы о «почти всех» графах. Тема 12. Планарные графы Планарные графы. Теоремы Эйлера и Куратовского о планарных графах. Алгоритм определения планарности в гамильтоновом графе (метод цикла). Тема 13. Раскраски графов Раскраски. Хроматическое число. Теорема о четырех цветах. Алгоритмы раскраски (точные и приближённые). Тема 14. Направленные, ориентированные графы Направленные, ориентированные графы. Полустепени вершин. Способы задания. Операции над направленными графами. Связность, типы связности направленных графов. Достижимость. Матрица достижимости. Тема 15. Взвешенные графы Взвешенные графы. Взвешенные направленные графы (сети). Кратчайшее остовное дерево в графе. Деревья Штейнера. Раздел 5. Основные прикладные задачи теории графов Тема 16. Нахождение кратчайшего остовного дерева в графе Нахождение кратчайшего остовного дерева в графе с помощью алгоритмов Краскала и Прима. Тема 17. Нахождение кратчайших путей в графах Нахождение кратчайших путей в графах. Алгоритм Дейкстры. Алгоритм Флойда. Тема 18. Нахождение максимального потока в графе Потоки в сетях. Задача о нахождении максимального потока в графе. Теорема и алгоритм Форда-Фалкерсона. Тема 19. Задача о назначениях Паросочетания в двудольных взвешенных графах. Задача о назначениях, венгерский метод решения. Тема 20. Задача о коммивояжёре Метод ветвей и границ. Задача о коммивояжёре. «Жадные» алгоритмы. КОНТРОЛЬНАЯ РАБОТА
1.(A Ç(( 2. (A Ç C)È(B Ç 3. (A \ B)È(A Ç B)È( 4. (A Ç C)È(A \ C)È 5. (A Ç B)È( 6. ((A \ B)È(A Ç B)) Ç ( 7. (A Ç B Ç C)È(C \ А)È( 8. 9. (A Ç B Ç C)È( 10.
II. С помощью основных равносильностей (без построения таблицы истинности) привести заданную булеву функцию к виду СДНФ.
11. 12. 13. 14. 15. III. Составить таблицу истинности для заданной булевой функции. По таблице истинности составить СДНФ, СКНФ этой булевой функции и получить представление этой булевой функции в виде полинома Жегалкина и арифметического полинома.
21. 22. 23. 24. 25.
IV. Построить по матрице смежности граф и его реберный граф.
31.
32.
33.
34.
35. V. Для изображенного графа записать последовательность степеней, построить матрицу смежности, найти центр и центр тяжести.
41. 46.
42. 47.
43. 48.
4
45. 50.
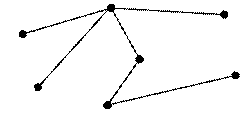
VI. Дайте развернутый (с пояснениями и, если это необходимо, с доказательствами) ответ на следующий вопрос: Является ли изображенный граф связным, полным, деревом, двудольным (если да, то разделить вершины на доли), эйлеровым, гамильтоновым(если является, то построить соответствующие циклы).
51.
56.
52. 57.
53. 58.
54. 59.
5
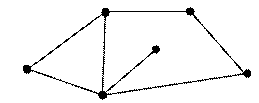
VII. С помощью алгоритма Флойда найти кратчайшие пути между всеми па
61.66.
62. 67.
63. 68
64. 69.
65. 70.
I. Докажите тождество Решение:
= = = = =
При преобразовании были использованы следующие формулы:
II. С помощью основных равносильностей (без построения таблицы истинности) привести заданную булеву функцию к виду СДНФ.
Решение. С помощью основных равносильностей преобразуем к ДНФ:
Применяя закон склеивания (в обратном порядке:
Т.к. III. Составить таблицу истинности для заданной булевой функции. По таблице истинности составить СДНФ, СКНФ этой булевой функции и получить представление этой булевой функции в виде полинома Жегалкина и арифметического полинома.
Решение. Составим таблицу истинности для этой булевой функции Таблица истинности СДНФ
СДНФ состоит из дизъюнкций полных элементарных конъюнкций наборов переменных
СКНФ состоит из конъюнкций полных элементарных дизъюнкций наборов переменных Таблица истинности СКНФ
Следовательно, СКНФ этой булевой функции имеет вид:
Получим представление этой булевой функции в виде полинома Жегалкина. Заменим в СДНФ операцию дизъюнкции операцией сложения по модулю два по
Все переменные с отрицанием заменяем по формуле
Т.е. P(F)
Найдем представление этой булевой функции в виде арифметического полинома. Заменим в СДНФ операцию дизъюнкции на операцию "арифметическое сложение" по формуле
Все переменные с отрицанием заменяем по формуле
Получаем, что G(F)
Ответ: СДНФ имеет вид:
IV. Построить по матрице смежности граф и его реберный граф.
Решение. По матрице смежности строим граф:
Строим реберный граф. Вершинами реберного графа являются ребра исходного графа. Вершины смежны, если смежны соответствующие им ребра исходного графа. Получаем следующий реберный граф:
V. Для изображенного графа записать последовательность степеней, построить матрицу смежности, найти центр и центр тяжести.
Решение. 1) Запишем последовательность степеней графа. deg A =1, deg D =1, deg B =2, deg E =4, deg C =1, deg F =3. Значит последовательность степеней графа имеет вид: (1, 1, 1, 2, 3, 4).
2) Постоим матрицу смежности:
3) Найдем эксцентриситеты вершин графа
Следовательно, центр графа составляют вершины B, E, F.
4) Найдем сумму расстояний для каждой вершины графа
Следовательно, центр тяжести графа находится в вершине Е. VII. С помощью алгоритма Флойда найти кратчайшие пути между всеми парами вершин графа.
Решение. Для выполнения алгоритма Флойда построим матрицу весов, которая является разновидностью матрицы смежности:
Выполним проход матрицы для каждой из вершин графа. Если путь через вершину прохода короче, то он и выбирается.
1) Проход через вершину А. С помощью построенной матрицы (а не по графу) сравниваем пути. Например, между вершинами C и E «расстояние»
2) Проход через вершину B. Выполняется аналогично, но основой для его выполнения служит матрица, полученная в результате прохода через матрицу А.
3) Проход через вершину С.
В результате этого прохода матрица не изменилась, так как в вершину С не входит ни одна дуга, а следовательно путь из одной вершины в другую через С невозможен.
4) Проход через вершину D.
5) Проход через вершину E.
В результате этого прохода матрица также как и для прохода через вершину С не изменилась, так как из вершины Е не выходит ни одна дуга, а следовательно путь из одной вершины в другую через Е невозможен.
Ответ: матрица расстояний между вершинами графа имеет вид
ЛИТЕРАТУРА 1 Горбатов, В. А. Дискретная математика / В. А. Горбатов, А. В. Горбатов, М. В. Горбатова. – М.: АСТ Астрель, 2006. 2 Горбатов, В. А. Основы дискретной математики / В. А. Горбатов. – М.: Высшая школа, 1986. 3 Новиков, Ф. А. Дискретная математика для программистов / Ф. А. Новиков. – СПб.: Питер, 2007. 4 Плотников, А. Д. Дискретная математика: учеб. пособие / А. Д. Плотников. – М.: Новое знание, 2006. 5 Супрун, В. П. Теория булевых функций. Теория автоматов. Полиномиальное разложение булевых функций: метод. указания к семинарским занятиям по специальным курсам / В. П.Супрун. – Мн.: БГУ, 1991. 6 Шапорев, С. Д. Дискретная математика. Курс лекций и практических занятий / С. Д. Шапорев. – СПб.: БХВ-Петербург, 2007. 7 Яблонский, С. В. Введение в дискретную математику / С. В.Яблонский. – М.: Наука,1988.
СОДЕРЖАНИЕ Введение…………………………………………………………………… 3 Варианты контрольных заданий…………………………………………..4 Рабочая программа…………………………….……………………….......5 Контрольная работа…………………………………………………………7 Решение типового варианта……………………………….………………12 Литература…………………………………………………………………..19
План 2009/2010, поз. 30
Петрович Ася Вениаминовна
Методические указания и контрольные задания по дисциплине «Дискретная математика» для студентов уровня ВО заочной формы обучения специальности 45. 01. 03 «Сети телекоммуникаций»
Редактор Вердыш Н.В.
Подписано к печати Формат Усл. Печ. Л. 1,5. Уч. - изд. Л. 1,3 Тираж 60 экз. Заказ
Высший государственный колледж связи 220114 г. Минск, Скорины 8, к. 2.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.189.25 (0.011 с.) |

 I. Докажите тождество
I. Докажите тождество )È(
)È( )))È(
)))È( ) = A.
) = A. )È(
)È( Ç C)È(
Ç C)È(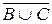 ) = U.
) = U. =U.
=U.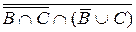 =
= 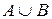 .
. )È(
)È( ))=U.
))=U. =Ø.
=Ø.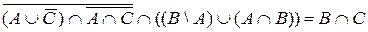 .
. =
=  .
. . 16.
. 16.  .
.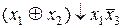 . 17.
. 17.  .
. . 18.
. 18.  .
.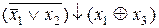 19.
19.  .
.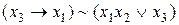 . 20.
. 20.  .
. . 26.
. 26.  .
. . 27.
. 27.  .
.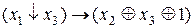 . 28.
. 28.  .
.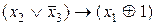 . 29.
. 29.  .
. . 30.
. 30. 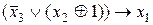 .
. . 36.
. 36.  .
. . 37.
. 37.  .
. . 38.
. 38.  .
. . 39.
. 39.  .
. . 40.
. 40.  .
.
















 рами вершин графа.
рами вершин графа. 





 .
.
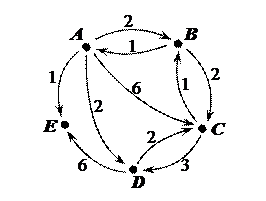

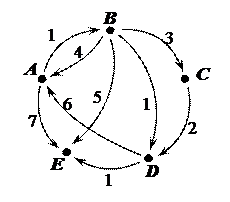
 =
=  .
. =
= =
=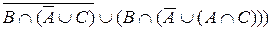 =
= =
= =
=  ,
, ,
,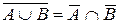 ,
, ,
, ,
, ,
,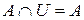 ,
, .
.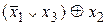 .
. =
=  =
=  =
= =
=  - ДНФ.
- ДНФ. ), дополняем конъюнкции
), дополняем конъюнкции 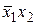 ,
,  до полных элементарных конъюнкций:
до полных элементарных конъюнкций: .
.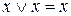 , после сокращения одинаковых конъюнкций, получаем СДНФ: F =
, после сокращения одинаковых конъюнкций, получаем СДНФ: F =  .
.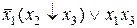








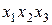
 , на которых функция принимает значение 1. Переменные берутся без отрицания, если им соответствует в таблице истинности 1, с отрицанием, если 0. Следовательно, СДНФ имеет вид:
, на которых функция принимает значение 1. Переменные берутся без отрицания, если им соответствует в таблице истинности 1, с отрицанием, если 0. Следовательно, СДНФ имеет вид: .
.

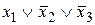
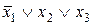
 (
( . При этом воспользуемся тем, что произведение (конъюнкция) любых полных дизъюнкций СДНФ всегда равно нулю (т.е.
. При этом воспользуемся тем, что произведение (конъюнкция) любых полных дизъюнкций СДНФ всегда равно нулю (т.е.  , если
, если  ). Следовательно, СПНФ будет иметь вид:
). Следовательно, СПНФ будет иметь вид: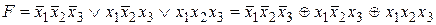 .
. , затем раскрываем скобки и из полученного выражения удаляем попарно одинаковые слагаемые:
, затем раскрываем скобки и из полученного выражения удаляем попарно одинаковые слагаемые:

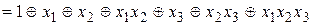 .
.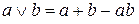 . При этом воспользуемся тем, что произведение (конъюнкция) любых полных дизъюнкций СДНФ всегда равно нулю (
. При этом воспользуемся тем, что произведение (конъюнкция) любых полных дизъюнкций СДНФ всегда равно нулю ( , если
, если  .
. , затем раскрываем скобки и в полученном выражении приводим подобные:
, затем раскрываем скобки и в полученном выражении приводим подобные: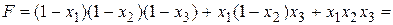

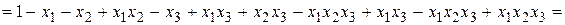

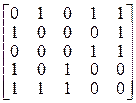 .
.




 ,
, ,
, ,
, ,
, ,
, .
.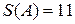






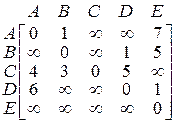 .
. , а путь C – А – E равен 11, поэтому меняем соответствующий элемент в матрице. Получаем следующую матрицу:
, а путь C – А – E равен 11, поэтому меняем соответствующий элемент в матрице. Получаем следующую матрицу: .
. .
. .
.


