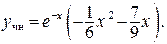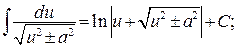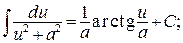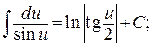Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения первого порядкаВВЕДЕНИЕ
Методические указания предназначены для студентов 2-го курса заочной формы обучения всех специальностей и содержат варианты заданий контрольной работы № 5 по теме: «Дифференциальные уравнения». Приведены краткие теоретические сведения и примеры выполнения заданий. Перед началом выполнения контрольной работы необходимо изучить теоретический материал, используя методические указания, конспекты установочных занятий и рекомендуемую литературу. Контрольная работа оформляется в отдельной тетради, регистрируется в деканате и передается на проверку преподавателю в установленные сроки.
ВАРИАНТЫ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ № 5
2. КРАТКИЙ СПРАВОЧНЫЙ МАТЕРИАЛ И ПРИМЕРЫ ВЫПОЛНЕНИЯ ЗАДАНИЙ ПО ТЕМЕ: Однородные уравнения
Однородные ДУ 1-го порядка имеют вид:
Это уравнение сводится к уравнению с разделяющимися переменными при помощи замены
После вычисления интеграла вместо z нужно подставить Пример 1.2. Найти общее решение ДУ
Решение. Разделим уравнение на Делаем замену
Найдем интегралы в левой и правой частях полученного равенства:
Итак, получим:
Линейные уравнения
Линейные ДУ 1-го порядка имеют вид:
где p (x) и q (x) — известные функции, непрерывные на некотором интервале. Такие уравнения обычно решают методом Бернулли, который состоит в следующем. Решение ищется в виде произведения двух функций
Объединим второе и третье слагаемые в левой части последнего уравнения, вынося U за скобки, и получим:
Поскольку одну неизвестную функцию у заменили двумя функциями U и V, то одну из этих функций можем взять произвольно. Выберем функцию V (x) так, чтобы она была решением уравнения
тогда вторая функция U (x) должна удовлетворять уравнению
Решив уравнение с разделяющимися переменными (7), найдем V и подставим его в (8), откуда найдем U. Общее решение получим как произведение найденных функций U и V:
Пример 1.3. Найти общее решение ДУ:
Решение. Уравнение имеет вид (5), поэтому является линейным. Решим его методом Бернулли. Сделаем замену
Приравняем коэффициент при U к нулю и получим: Решим первое из полученных уравнений:
Полученную функцию
Таким образом,
Уравнения Бернулли
Уравнения Бернулли имеют вид:
где Метод решения таких уравнений тот же, что и для линейных уравнений. Пример 1.4. Найти общее решение ДУ:
Решение. Разделим уравнение на
Полученное уравнение имеет вид (9), следовательно, это уравнение Бернулли. Сделаем замену
Приравняем коэффициент при U нулю и получим: Решим первое уравнение:
Подставим полученную функцию V во второе уравнение:
(использовали формулы 3 а и 9 таблицы интегралов). Таким образом, общее решение ДУ:
Случай V = 0 и Все рассмотренные типы ДУ 1-го порядка и методы их решения включены в таблицу ДУ 1-го порядка (см. прил. 2).
Решение. а)
Решим его, используя формулу корней квадратного уравнения:
Получим корни:
Поскольку
б) Характеристическое уравнение:
его корни найдем по формулам (20):
Поскольку
в) Характеристическое уравнение:
его корни найдем по формуле (20):
Получили комплексно сопряженные корни вида Решение запишем в виде (19):
г) Характеристическое уравнение:
Решим его:
2.2.3. Линейные неоднородные дифференциальные уравнения
Линейные неоднородные ДУ 2-го порядка имеют вид:
Здесь Согласно теореме о структуре общего решения линейного неоднородного ДУ общее решение ДУ (21)
Рассмотрим, в каком виде можно искать частное решение Пусть
где Тогда частное решение
где k — кратность корня
При этом Пример 2.3. Найти общее решение линейных неоднородных ДУ 2-го порядка с постоянными коэффициентами: а) Решение. а) Найдем общее решение соответствующего однородного ДУ:
Характеристическое уравнение:
Поскольку
Найдем частное решение неоднородного уравнения. Правая часть уравнения Сравнивая ее с видом (23)
Коэффициенты А и В определим из условия, что функция у чн — решение уравнения и поэтому должна ему удовлетворять. Найдем
и подставим в исходное уравнение:
Приравняем коэффициенты при
Итак, Тогда согласно (22) общее решение неоднородного ДУ имеет вид:
б) Найдем общее решение соответствующего однородного ДУ:
Характеристическое уравнение:
Найдем его корни по формуле (20):
Поскольку
Найдем частное решение неоднородного уравнения. Правая часть уравнения
Для определения коэффициентов А и В найдем
и подставим в исходное уравнение:
Разделим обе части уравнения на
Приравняем коэффициенты при одинаковых степенях х в правой и левой частях уравнения:
Итак, Тогда согласно (22) общее решение неоднородного ДУ имеет вид:
ПРИЛОЖЕНИЯ Приложение 1 Таблица основных интегралов
Приложение 2 ЛИТЕРАТУРА 1. Кудрявцев В.А., Демидович В.П. Краткий курс высшей математики. — М.: Наука, 1998. — 656 с. 2. Баврин И.И. Высшая математика. — М.: ACADEMIA, 2002. — 616 с. 3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 т. Т. 2. — М.: Высш. шк., 1998. — 304 с. 4. Высшая математика для экономистов / Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2000. — 471 с. 5. Практикум по высшей математике для экономистов / Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003. — 423 с.
ВВЕДЕНИЕ
Методические указания предназначены для студентов 2-го курса заочной формы обучения всех специальностей и содержат варианты заданий контрольной работы № 5 по теме: «Дифференциальные уравнения». Приведены краткие теоретические сведения и примеры выполнения заданий. Перед началом выполнения контрольной работы необходимо изучить теоретический материал, используя методические указания, конспекты установочных занятий и рекомендуемую литературу. Контрольная работа оформляется в отдельной тетради, регистрируется в деканате и передается на проверку преподавателю в установленные сроки.
ВАРИАНТЫ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ № 5
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.12.248 (0.012 с.) |

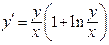

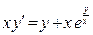








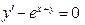









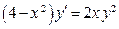




























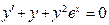
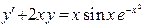

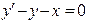




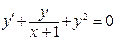













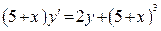





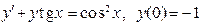


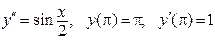
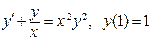








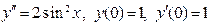
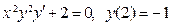






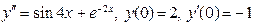
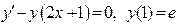










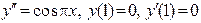


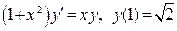








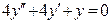












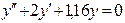

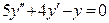




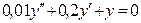






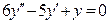








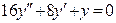









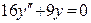

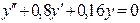


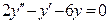
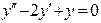




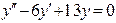
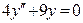

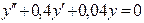







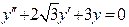







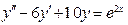

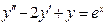


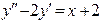
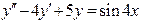


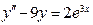




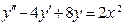

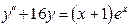

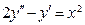
 (4)
(4) где
где  Действительно, подставляя в уравнение (4)
Действительно, подставляя в уравнение (4) 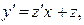 получаем:
получаем:  — уравнение с разделяющимися переменными. Разделяя переменные, получим
— уравнение с разделяющимися переменными. Разделяя переменные, получим

 и, если можно, упростить полученное выражение.
и, если можно, упростить полученное выражение.
 (х = 0 не принадлежит ООУ) и получим:
(х = 0 не принадлежит ООУ) и получим:  — однородное уравнение вида (4) в котором
— однородное уравнение вида (4) в котором 
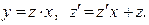 Тогда исходное уравнение становится уравнением с разделяющимися переменными:
Тогда исходное уравнение становится уравнением с разделяющимися переменными:

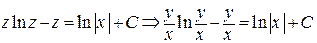 — общий интеграл исходного ДУ.
— общий интеграл исходного ДУ. (5)
(5) Тогда
Тогда 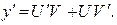 Подставляя y и y ¢ в (5), получим:
Подставляя y и y ¢ в (5), получим:
 (6)
(6) (7)
(7) (8)
(8)
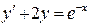




 (при интегрировании использовали формулы 4 и 2 таблицы интегралов). При нахождении V постоянную С полагаем равной нулю, так как в данном случае достаточно найти некоторое решение.
(при интегрировании использовали формулы 4 и 2 таблицы интегралов). При нахождении V постоянную С полагаем равной нулю, так как в данном случае достаточно найти некоторое решение. подставим во второе уравнение:
подставим во второе уравнение: (использовали формулы 2 и 7 таблицы интегралов).
(использовали формулы 2 и 7 таблицы интегралов). или
или 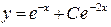 — общее решение исходного ДУ.
— общее решение исходного ДУ. (9)
(9)
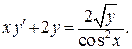

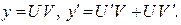 Получим:
Получим:

 (использовали формулу 4 таблицы интегралов).
(использовали формулу 4 таблицы интегралов).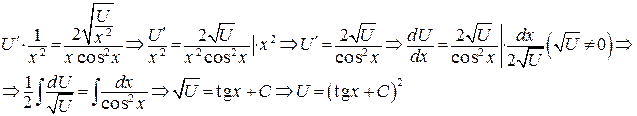

 y = 0 является решением ДУ, и так как оно не может быть получено из общего решения, то является особым решением.
y = 0 является решением ДУ, и так как оно не может быть получено из общего решения, то является особым решением. Составим характеристическое уравнение:
Составим характеристическое уравнение:
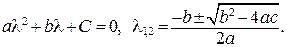 (20)
(20)
 и
и  то общее решение запишем в виде (17):
то общее решение запишем в виде (17):



 то общее решение запишем в виде (18):
то общее решение запишем в виде (18):



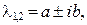 где а = 1, b = 4.
где а = 1, b = 4.



 — комплексно сопряженные корни вида
— комплексно сопряженные корни вида 

 (21)
(21) — известная функция, непрерывная на некотором промежутке.
— известная функция, непрерывная на некотором промежутке. есть сумма общего решения
есть сумма общего решения  соответствующего однородного уравнения (15) и любого частного решения
соответствующего однородного уравнения (15) и любого частного решения 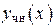 неоднородного уравнения (21), т. е.
неоднородного уравнения (21), т. е. (22)
(22) и
и  корни характеристического уравнения (16), а правая часть уравнения имеет вид:
корни характеристического уравнения (16), а правая часть уравнения имеет вид: (23)
(23) — многочлены от х степеней n и m соответственно с известными коэффициентами.
— многочлены от х степеней n и m соответственно с известными коэффициентами. следует искать в виде:
следует искать в виде: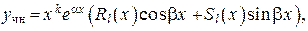 (24)
(24)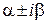 характеристического уравнения:
характеристического уравнения:
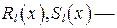 многочлены от х степени
многочлены от х степени  с
с  и
и  находят методом неопределенных коэффициентов.
находят методом неопределенных коэффициентов. б)
б) 





 заключаем, что
заключаем, что  Определим параметры частного решения (24). Учитывая, что
Определим параметры частного решения (24). Учитывая, что  а
а  получим, что
получим, что 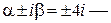 не является корнем характеристического уравнения, поскольку корни
не является корнем характеристического уравнения, поскольку корни  Следовательно, k = 0. Найдем
Следовательно, k = 0. Найдем  Следовательно, порядок многочленов R и S равен 0, т. е. R 0 = A, а S 0 = B, где А и В — некоторые неизвестные пока коэффициенты. Подставив полученные параметры в
Следовательно, порядок многочленов R и S равен 0, т. е. R 0 = A, а S 0 = B, где А и В — некоторые неизвестные пока коэффициенты. Подставив полученные параметры в  имеем:
имеем:
 и
и 


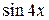 и
и  в правой и левой частях полученного равенства:
в правой и левой частях полученного равенства: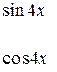







 Сравнивая ее с видом (23)
Сравнивая ее с видом (23)  Определим параметры частного решения (24). Учитывая, что
Определим параметры частного решения (24). Учитывая, что  а
а  получим, что
получим, что 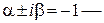 однократный корень характеристического уравнения, поскольку корни
однократный корень характеристического уравнения, поскольку корни  Следовательно, k = 1. Найдем
Следовательно, k = 1. Найдем  Следовательно, порядок многочленов R и S равен 1, т. е.
Следовательно, порядок многочленов R и S равен 1, т. е. 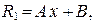 а
а  где А, В, С, D — неизвестные коэффициенты. Подставляя полученные параметры в
где А, В, С, D — неизвестные коэффициенты. Подставляя полученные параметры в 


 и приведем подобные члены:
и приведем подобные члены: