
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение в полных дифференциалах (определение, общий интеграл).Содержание книги
Поиск на нашем сайте
Необходимое и достаточное условие для того чтобы уравнение было уравнением в полных дифференциалах. Интегрирующий множитель. Уравнение с разделяющимися переменными. Однородное уравнение. Линейное дифференциальное уравнение первого порядка. Уравнение Бернулли. Уравнение Риккати. Система дифференциальных уравнений, решение, общее решение. Комплексные решения. Теорема существования и единственности для систем дифференциальных уравнений. Теоремы существования и единственности для уравнения n-го порядка и для линейных систем дифференциальных уравнений. 14.Функция Линейное дифференциальное уравнение n-го порядка. Свойства многочленов символа p. Общее решение линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами (случай простых корней). Необходимые и достаточные условия для того чтобы число l было k кратным корнем многочлена. Общее решение линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами (случай кратных корней). Выделение вещественных решений. Математический маятник. Устойчивые многочлены. Оценка решений с устойчивым характеристическим многочленом. Устойчивость многочленов 1 и 2 -го порядков. Необходимое условие устойчивости вещественного многочлена. Критерий Рауса-Гурвица. Устойчивость многочлена третьего порядка. Линейное неоднородное дифференциальное уравнение n-го порядка. Структура общего решения. Квазиполином, структура общего решения с правой частью в виде квазиполинома. Частные решения уравнения со специальной правой частью. Метод комплексных амплитуд. Линейное дифференциальное уравнение n-го порядка с переменными коэффициентами. Линейное однородное уравнение и его свойства. Линейная зависимость функций. 27. Определитель Вронского и его применение для определения линейной зависимости решений линейных дифференциальных уравнений. Фундаментальная система решений и ее свойства. Восстановление линейного дифференциального уравнения по его фундаментальной системе. Формула Остроградского-Лиувилля.
Понижение порядка дифференциального уравнения. Метод вариации произвольных постоянных. 32. Двухточечная краевая задача и ее преобразования. Построение функции Грина и вывод ее свойств. Необходимое и достаточное условие существования функции Грина. Задача о собственных значениях краевой задачи. E - решения. Существование e - решений. Ломаные Эйлера. Теорема Пеано. Теорема единственности решения.
Второй семестр 1. Линейная система дифференциальных уравнений с переменными коэффициентами, формы записи. Теорема существования и единственности. (без доказательства). Линейная однородная система, два свойства. Фундаментальная система решений ее существование и общее решение ЛО системы ДУ. Определитель Вронского и его свойства. Формула Лиувилля. Матричное ДУ и его связь с векторным ДУ. Фундаментальная матрица. Свойства фундаментальных матриц. Сопряженное ДУ. Фундаментальная матрица сопряженного ДУ. Формула для решения задачи Коши линейной неоднородной системы ДУ. Тождество Лагранжа. Сходимость матричных последовательностей и рядов. Признак Вейерштрасса о равномерной сходимости матричного ряда. Матричная экспонента и ее свойства. Решение ЛСДУ с постоянными коэффициентами в случае простых собственных значений. Решение ЛСДУ с постоянными коэффициентами в общем случае. Выделение вещественных решений. Формула для решения задачи Коши ЛНСДУ с постоянными коэффициентами. Эквивалентность норм в конечномерном пространстве. Оценка нормы матричной экспоненты. Логарифм матрицы и его существование. Теорема Флоке-Ляпунова.
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.244.34 (0.007 с.) |

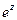 и ее свойства.
и ее свойства.


