
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика обработки результатов прямых измеренийСодержание книги
Поиск на нашем сайте
Теперь мы можем приступить к изучению элементарных правил обработки экспериментальных данных. Начнём с самой простой и одновременно важнейшей методики обработки результатов прямых измерений. Обозначим через Поскольку,
Тогда, ошибка отдельного измерения (
Зная ошибку каждого измерения, следующим шагом найдем, так называемое среднеквадратическое отклонение среднего
(Внимание! Среднеквадратическое отклонение среднего Формула для вычисления
Оказывается, что при проведении новых серий экспериментов, следующие средние значения Вероятность Однако 68% невысокая вероятность. В подавляющем большинстве случаев требуется знать интервал
Обработка случайных погрешностей прямых измерений сводится к нахождению В лабораториях физики МГТУ принят государственный стандарт, в соответствии с которым Таблица коэффициентов Стьюдента для доверительной вероятности
Полная погрешность измерений
Как только найдена полная ошибка, обработка погрешностей закончена. Записываем ответ:
Рядом необходимо указать относительную погрешность
выраженную в процентах ( Внимание, относительная погрешность ε превышающая 10%-15% свидетельствует о недостаточном усердии учащегося при выполнении лабораторной работы. Заметим, что Пример 2: Пусть Пренебрегая Определим относительную ошибку, которую мы совершаем, пренебрегая
Пример 3, когда инструментальная погрешность превышает случайный разброс Отметим также, что в случае однократных измерений вычисление
§2
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.12.122 (0.009 с.) |

 измеряемую физическую величину. Пусть в результате нескольких опытов получено n пронумерованных значений
измеряемую физическую величину. Пусть в результате нескольких опытов получено n пронумерованных значений  (i – номер измерения, i = 1,2,3,…,n). Зададимся вопросом: Какую ошибку
(i – номер измерения, i = 1,2,3,…,n). Зададимся вопросом: Какую ошибку 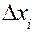 мы допустили в каждом отдельном измерении? При известном истинном значение
мы допустили в каждом отдельном измерении? При известном истинном значение  , решение очевидно
, решение очевидно  .
.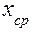 , которое легко найти по известной формуле.
, которое легко найти по известной формуле.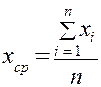 или
или  . (1)
. (1)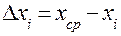 (2)
(2) :
: или
или  . (3)
. (3)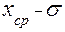 ,
, 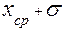 .
.
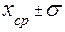 с вероятностью 68%.
с вероятностью 68%. , с которой среднее значение попадает в некоторый интервал, называется доверительной вероятностью, при этом интервал называют доверительным интервалом
, с которой среднее значение попадает в некоторый интервал, называется доверительной вероятностью, при этом интервал называют доверительным интервалом  .
. , зависящие от числа измерений
, зависящие от числа измерений 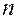 и доверительной вероятности
и доверительной вероятности  (4)
(4)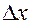 складывается из доверительного интервала и инструментальной погрешности. Теория вероятности дает следующую формулу:
складывается из доверительного интервала и инструментальной погрешности. Теория вероятности дает следующую формулу: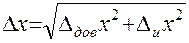 (5)
(5) , (6)
, (6)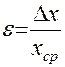 , (7)
, (7)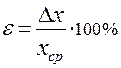 ) (8)
) (8) превышает другую в 3 и более раз, то меньшей можно пренебречь.
превышает другую в 3 и более раз, то меньшей можно пренебречь. ;
; 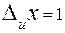 , тогда:
, тогда:  .
. , получим
, получим  .
.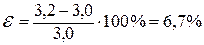 , следовательно, действие допустимо.
, следовательно, действие допустимо. . При измерении штангенциркулем диаметра шариков подшипника были получены следующие результаты: 13,2мм; 13,1мм; 13,2мм; 13,1мм; 13,1мм; 13,1мм. Очевидно, что все измеренные значения лежат внутри интервалов
. При измерении штангенциркулем диаметра шариков подшипника были получены следующие результаты: 13,2мм; 13,1мм; 13,2мм; 13,1мм; 13,1мм; 13,1мм. Очевидно, что все измеренные значения лежат внутри интервалов  мм или
мм или  мм. Инструментальная погрешность отдельного измерения
мм. Инструментальная погрешность отдельного измерения  (легко проверить
(легко проверить  ). Причина в том, что случайные изменения диаметра слишком малы по сравнению с погрешностью штангенцуркуля.
). Причина в том, что случайные изменения диаметра слишком малы по сравнению с погрешностью штангенцуркуля.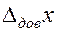 бессмысленно. В этом случае полную погрешность принимают равной инструментальной
бессмысленно. В этом случае полную погрешность принимают равной инструментальной 


