
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 7 расчет частотных и переходных характеристик систем автоматического регулированияСодержание книги
Поиск на нашем сайте Цель Изучить способы анализа систем автоматического регулирования (САР) путем расчета и построения частотных и переходных характеристик. Задание Требуется выполнить указанные ниже этапы работы. Вариант работы назначается или выбирается по номеру зачетной книжки как в лабораторной работе №5. 7.1. Для каждого из звеньев, указанных на рис. 7.1 и выполненных на базе операционного усилителя, найти передаточную функцию. Указать к какому типу типовых звеньев относится данное звено. 7.2. Составить структурную схему с указанием передаточных функций каждого звена и определить общую передаточную функцию всей системы W 0. 7.3. Построить амплитудно-фазовую (годограф), амплитудно-час-тотную, фазочастотную и логарифмическую частотную характеристики. 7.4. По виду передаточной функции W 0 построить логарифмическую асимптотическую частотную характеристику (ЛАЧХ). 7.5. Построить график переходного процесса (переходную характеристику) при единичном входном ступенчатом воздействии и определить время переходного процесса – время регулирования Тр – с погрешностью δ = 5 %. 7.6. Проверить полученные результаты моделированием в среде Workbench. В отчете привести расчеты, табличные и графические результаты. Методические указания и пример расчета В общем виде типовые элементы электронной автоматики, выполненные на базе операционного усилителя, имеют структуру, показанную на рис. 7.3. На этом рисунке операционный усилитель (ОУ) имеет внешние цепи с комплексным сопротивлением z 0 и z 1, причем z 1 – сопротивление на входе элемента, а z 0 – сопротивление цепи обратной связи. Сопротивления z 0 и z 1 комплексные, т.к. в общем случае содержат, кроме резисторов с активным сопротивлением, емкостные и индуктивные элементы цепей с соответствующими реактивными сопротивлениями. Именно поэтому расчет схем на базе операционных усилителей удобно выполнять в комплексной форме с использованием преобразования Лапласа. Комплексные сопротивления отдельных элементов электронных цепей приведены в табл. 7.1 (позиции 1–3). Там же приведены выражения для полных комплексных сопротивлений при параллельном (позиция 4) и последовательном (позиция 5) соединении элементов с комплексными сопротивлениями z 1 и z 2.
Таблица 7.1
Пользуясь приведенными в табл. 7.1 соотношениями, можно определить полное комплексное сопротивление любой электронной цепи и рассчитать, в частности, сопротивления Z0 и Z1 схемы, показанной на рис. 7.3. Для этого вместо каждого электронного элемента цепи записывается его комплексное сопротивление в соответствии с позициями 1–3, табл. 7.1, а полное сопротивление рассчитывается в соответствии с позициями 4–5. Рассчитав сопротивления Z 0 и Z 1, определяют передаточную функцию W (p) звена по следующей формуле:
Рис. 7.1. Схемы звеньев САР на базе операционного усилителя
Варианты схем САР приведены на рис. 7.2: Знак «–» в формуле (7.1) ставится тогда, когда операционный усилитель является инвертирующим, т.е. его выходное напряжение имеет противоположный знак по отношению ко входному. Это условие выполняется практически наиболее часто. Когда же выходное сопротивление неинвертировано – знак «–» опускается. Дальнейший путь расчета и исследования электронных схем автоматики – приведение выражения (7.1) к виду
где
Рис. 7.2. Варианты схем систем автоматического регулирования
Окончание рис. 7.2
Затем определяют известными из теории автоматического управления методами характеристики САР, влияющие на эффективность и качество ее функционирования. на практике часто встречаются типовые динамические звенья (табл. 7.2), описываемые дифференциальными уравнениями не выше второго порядка. Для улучшения характеристик в электронные системы автоматического управления (САУ) вводят обратные связи, которые обеспечивают воздействие выходного сигнала на входной. Для этого может быть использован сумматор (звено 1 на рис. 7.1), на вход которого поступают входной сигнал и сигнал обратной связи. Если сигнал обратной связи является неинвертированным, или синфазным, по отношению к входному сигналу, то образуется положительная обратная, связь, так как указанные сигналы суммируются с одинаковыми знаками, а если инвертированным – то отрицательная. Например, в варианте 0 на рис. 7.2 к сумматору подводится сигнал обратной связи, сформированный при прохождении через нечетное количество инвертирующих усилителей. Обратная связь в таком случае является отрицательной. Отрицательная (ООС) и положительная (ПОС) обратная связь на структурных схемах изображается следующими знаками соответственно:
После определения вида обратной связи расчеты проводят по выражениям (7.4) или (7.5), но уже без учета инвертирования входящими ОУ, т.е. по модулю. Приведем пример начального расчета задания для звена на базе ОУ, показанного на рис. 7.3.
Рис. 7.3. Пример звена для расчета
Определим передаточную функцию:
Комплексное сопротивление
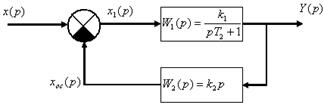
где Полученная передаточная функция является суммой передаточных функций типового безынерционного звена (табл. 7.2, позиция 1) и идеального интегратора (табл. 7.2, позиция 5). После определения передаточных функций, всех звеньев в варианте задания и вида обратных связей составляют структурную схему. На рис. 7.4 показана составленная для примера структурная схема.
Рис. 7.4. Пример представления структурной схемы
Таблица 7.2
Типовые динамические значения
Передаточная функция всей системы при последовательном соединении звеньев
при параллельном соединении звеньев
при отрицательной обратной связи
при положительной обратной связи
Определим, например, передаточную функцию системы, показанной на рис. 7.4. Пользуясь выражением для соединения с отрицательной обратной связью (7.4), получим
где Для определения частотных характеристик системы переходят от передаточной функции W(p) к комплексной частотной передаточной функции W ( Далее выделяют в функции W (i ω), вещественную часть и мнимую, содержащую
где Например, для рассматриваемого примера находим частотную передаточную функцию и ее вещественную и мнимую части:
где
При преобразованиях знаменатель и числитель домножались на комплексное выражение (комплексное число), сопряженное знаменателю, и учитывалось, что
Амплитудно-фазовая характеристика (АФХ) строится на комплексной плоскости в координатах P ( Например, АФХ (годограф) показана на рис. 7.5. Зависимость от частоты отношения амплитуды выходного сигнала к амплитуде входного называется амплитудно-частотной характеристикой (АЧХ). Для ее построения необходимо найти модуль комплексной частотной характеристики W (i ω):
Зависимость от частоты фазового сдвига, получаемого сигналом после прохождения на выход, называется фазочастотной характеристикой (ФЧХ). Для ее построения находят аргумент комплексной частотной функции:
Рис. 7.5. Построение ЛАЧХ
Продолжим расчет рассматриваемой схемы. По выражениям (7.7), (7.8), используя (7.6), определим АЧХ и ФЧХ:
По результатам расчета строят графики. Примечание. При расчетах нужно учитывать выражения для постоянной времени:
Логарифмические характеристики строятся в координатах Следует отметить общую особенность построения графиков логарифмических частотных характеристик: значение Частоты сопряжения Построение переходной характеристики для единичного ступенчатого входного воздействия основано на переходе во временную область от выражения
Выражение (7.10) описывает выходную величину H(p), когда на вход САР с передаточной функцией W(p) подано единичное ступенчатое воздействие, изображением которого есть 1/ p. Переходя от выражения (7.10) во временную область, получают выражение для переходной характеристики – реакцию системы на единичное ступенчатое входное воздействие:
Знак L Для не очень сложных передаточных функций обратное преобразование осуществляют либо по таблицам обратных преобразований Построив графически переходную характеристику, определяют время переходного процесса как время входа в зону с указанной погрешностью отклонения δ. Используем для обратного преобразования Лапласа разложение Хевисайда для рациональных алгебраических функций в случае простых корней [22, c. 234] в виде
где Пример расчета Поясним расчет на примере САР, содержащей звенья на ОУ
7.1. Определяем передаточные функции для звеньев (из рис. 7.1). Звено № 1 - сумматор. Передаточная функция:
Звено № 2 Передаточная функция:
где По виду передаточной функции определяем, что звено безынерционное. Звено № 3 Передаточная функция:
где По табл. 7.2 определяем, что звено идеальное интегрирующее. Для остальных звеньев приводим окончательные результаты. Звено № 4:
где k 4 = –0,5 – идеальное дифференцирующее звено. Звено № 5
где k 5 = –0,1, T 5 = 0,01 – инерционное дифференцирующее. Звено № 6
где k 6 = –1, 7.2. Для составления структурной схемы определяем вид обратной связи (отрицательная или положительная). Так как в цепи обратной связи 1-1-2-5-2 и 1-2-4 нечетное количество блоков с инвертирующими операционными усилителями (пять блоков и три блока соответственно), то это определяет отрицательные обратные связи (если бы было четное количество операционных усилителей, обратные связи были бы положительными). Тогда схему с учетом определения обратных связей, как отрицательных обратных связей, можно представить в виде
В дальнейшем расчете теперь можно использовать значения для передаточных функций всех звеньев входящих в схему по модулю (т.е. не учитывать знак минус для передаточных функций каждого звена). Рассчитываем передаточную функцию W 24(p) для звеньев 1_2_4, соединенных с отрицательной обратной связью, по выражению (7.4):
где Получаем следующую расчетную структурную схему:
Рассчитываем передаточную функцию W 245(p) для последовательно соединенных звеньев W 24(p) и 5 по выражению (7.2).
где Получаем следующую расчетную структурную схему:
Рассчитываем общую передаточную функцию W 0(p) для соединения с отрицательной обратной связью по выражению (7.4):
Для получения окончательного вида находим корни квадратного уравнения в знаменателе:
Окончательный вид общей передаточной функции будет таким:
где
Полученное выражение для передаточной функции W 0(p) характеризует собой инерционное дифференцирующее звено. Рассчитываем комплексную передаточную функцию К комплексной передаточной функции переходим формальной заменой
Для устранения комплексного значения i в знаменателе умножаем числитель и знаменатель на сопряженные комплексные выражения и делим действительную и мнимые части полученного выражения:
После преобразований получим
Используя полученные выражения для АФХ (годограф) строится на комплексной плоскости в координатах Логарифмическая частотная характеристика (ЛЧХ) рассчитывается по выражению и строится в логарифмических координатах по оси частот по декадам, т.е. при десятикратном изменении частоты
Логарифмическая частотная характеристика (ЛАЧХ)
Переходная характеристика
Корни характеристического выражения знаменателя:
Используем для перехода от изображения к оригиналу для расчета
Из графика h (t) определяем на уровне 5% от максимального Построение логарифмической асимптотической частотной характеристики (ЛАЧХ) делается по виду передаточной функции и изменению текущего угла наклона ЛАЧХ в точках сопряжения. Передаточную функцию нужно перед этим привести к одному из трех возможных видов:
Количество скобок вида При этом начальный угловой коэффициент наклона определяется так: – для передаточной функции W (p) вида (7.11) угловой коэффициент наклона равен 0 дБ/дек (децибел на декаду), т.е. ЛАЧХ проходит горизонтально при очень низких частотах – для вида (7.12) угловой коэффициент наклона равен 20 дБ/дек, т.е. ЛАЧХ вначале при очень низких частотах – для вида (7.13) угловой коэффициент наклона равен – 20 дБ/дек, т.е. ЛАЧХ вначале при очень низких частотах Во всех случаях дальнейшее изменение угла наклона происходит в точках сопряжениях. Они определяются для каждой из скобок вида
В каждой из таких частот сопряжения В нашем примере находим все частоты сопряжения и расставляем их на оси частот (рис. 7.5):
Так как передаточная функция относится к виду (7.12), то ее начальный угловой коэффициент наклона равен +20 дБ/дек. При частоте При построении приближаем, перемещая по вертикали, ЛАЧХ
Проверяем аналитические расчеты, моделируя САР в Workbench. Для этого составляем общую электрическую принципиальную схему САР и набираем ее в Workbench. Подключаем body plotter для частотного анализа и генератор прямоугольных колебания для получения реакции на прямоугольное ступенчатое воздействие, т.е. для получения формы переходной характеристики. Для примера участок схемы одного из вариантов выглядит так (рис. 7.6).
Рис. 7.6. Исследование САР в Workbench
Контрольные вопросы и задания
7.1. Что такое преобразования Лапласа? Приведите выражение для прямого и обратного преобразования Лапласа. 7.2. Поясните графически правила построения логарифмической асимптотической частотной характеристики (ЛАЧХ) для своего задания. 7.3. Приведите графики результатов анализа САР в Workbench и копии экранов выполнения своего задания.
Вопросы для самопроверки 7.1. Какие условия применимости обратного преобразования Лапласа в форме разложения Хевисайда? 7.2. Какие еще программные средства для исследования САР Вам известны? 7.3. Какая из выполненных лабораторных работ является наиболее интересной?
П р и л о ж е н и е ОПИСАНИЕ ОСНОВНЫХ ЭЛЕМЕНТОВ
На рис. П1 представлена панель инструментов «Indicators», которая включает в себя элементы индикации, которые можно разместить на схеме. В табл. П1 рассмотрены некоторые из них.
Рис. П1. Панель инструментов «Indicators»
Таблица П1
Описание элементов панели инструментов «Indicators»
Окончание табл. П1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |








 . (7.1)
. (7.1)
 ,
, .
.



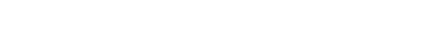







 – для ООС
– для ООС  – для ПОС.
– для ПОС.
 .
. определим в соответствие с табл. 7.1. (позиции 1, 2, 5):
определим в соответствие с табл. 7.1. (позиции 1, 2, 5):

 ,
,  .
.














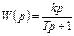

 определяется с учетом соединений ее звеньев по следующим правилам:
определяется с учетом соединений ее звеньев по следующим правилам: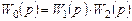 ; (7.2)
; (7.2) ; (7.3)
; (7.3) ; (7.4)
; (7.4) . (7.5)
. (7.5)
 .
. ) путем формальной замены переменной
) путем формальной замены переменной  на
на  .
. :
: ,
,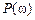 и
и  – вещественная и мнимая частотная характеристики, соответственно.
– вещественная и мнимая частотная характеристики, соответственно. ;
;
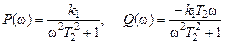 . (7.6)
. (7.6)
 ) и i
) и i  для различных значений циклической частоты
для различных значений циклической частоты  .
. . (7.7)
. (7.7) arctg
arctg  . (7.8)
. (7.8)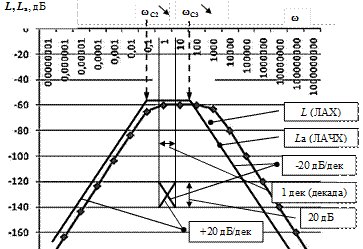

 .
. . (7.9)
. (7.9)
 и
и  на оси абсцисс находится в (–¥) из-за логарифмического масштаба.
на оси абсцисс находится в (–¥) из-за логарифмического масштаба. являются характерными точками изменения наклона асимптотической ЛАХ. В каждой из частот сопряжения
являются характерными точками изменения наклона асимптотической ЛАХ. В каждой из частот сопряжения  комплексной частотной передаточной функции
комплексной частотной передаточной функции  , происходит изменение текущего угла наклона асимптотической ЛАХ на ±20 дБ/дек. Указанной закономерностью пользуются для построения асимптотической ЛАХ, непосредственно по виду передаточной функции
, происходит изменение текущего угла наклона асимптотической ЛАХ на ±20 дБ/дек. Указанной закономерностью пользуются для построения асимптотической ЛАХ, непосредственно по виду передаточной функции  . Это позволяет строить асимптотические ЛАХ без проведения достаточно сложных математических преобразований, ориентируясь лишь на вид передаточной функции.
. Это позволяет строить асимптотические ЛАХ без проведения достаточно сложных математических преобразований, ориентируясь лишь на вид передаточной функции. . (7.10)
. (7.10) .
.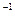 в выражении обозначает обратное преобразование Лапласа.
в выражении обозначает обратное преобразование Лапласа.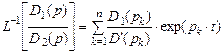 ,
, – знаменатель отношения многочленов, в котором опускаются сомножители вида
– знаменатель отношения многочленов, в котором опускаются сомножители вида  , для значений корней
, для значений корней  .
.

 ;
; 
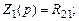


 ;
; 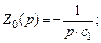




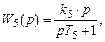

 – инерционное.
– инерционное.




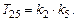

 .
.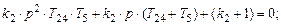



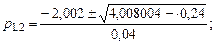
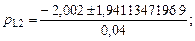





 и мнимую
и мнимую  части выражения
части выражения



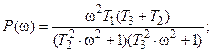

 , рассчитываем остальные частотные характеристики.
, рассчитываем остальные частотные характеристики. и
и  .
. , дБ.
, дБ. строится на одном графике (совместно) с логарифмической частотной характеристикой
строится на одном графике (совместно) с логарифмической частотной характеристикой  . Для ее построения понадобятся частоты сопряжения
. Для ее построения понадобятся частоты сопряжения  , которые определяются из скобок
, которые определяются из скобок  выражения для общей передаточной функции W (p):
выражения для общей передаточной функции W (p): и
и  .
. реакция системы на единичное ступенчатое воздействие и ее изображение по Лапласу
реакция системы на единичное ступенчатое воздействие и ее изображение по Лапласу  рассчитываются следующим образом:
рассчитываются следующим образом:

 .
. обратное преобразование Лапласа – разложение Хевисайда:
обратное преобразование Лапласа – разложение Хевисайда:





 ; (7.11)
; (7.11) ; (7.12)
; (7.12) . (7.13)
. (7.13) может быть любым (от 0).
может быть любым (от 0). Начальное положение ЛАЧХ равно
Начальное положение ЛАЧХ равно  , K – из выражения (7.11);
, K – из выражения (7.11); возрастает. Начальное положение ЛАЧХ неизвестно, т.е. будет построен общий характер изменения ЛАЧХ. В реальном случае кривая будет смещена по вертикали вниз или вверх. Для определения точного начального положения нужен или расчет, или ЛАЧХ проводят, приближая к раcсчитанной ЛАХ;
возрастает. Начальное положение ЛАЧХ неизвестно, т.е. будет построен общий характер изменения ЛАЧХ. В реальном случае кривая будет смещена по вертикали вниз или вверх. Для определения точного начального положения нужен или расчет, или ЛАЧХ проводят, приближая к раcсчитанной ЛАХ; :
: . (7.14)
. (7.14) происходит изменение текущего угла наклона на
происходит изменение текущего угла наклона на  дБ/дек, причем если скобка из которой определена частота сопряжения
дБ/дек, причем если скобка из которой определена частота сопряжения 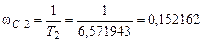 – из знаменателя,
– из знаменателя,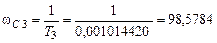 – из знаменателя.
– из знаменателя. он изменится на –20 дб/дек, так как найден для скобки из знаменателя (показано стрелкой вниз справа от
он изменится на –20 дб/дек, так как найден для скобки из знаменателя (показано стрелкой вниз справа от  он также изменится на
он также изменится на 










