Территория пристанционного участка

Пример устойчивого решения

 

Вводится термин "стабильное решение" как перевод словосочетания "stable solution". Термин "стабильное решение" напрямую связан с анализом чувствительности (sensitivity analysis) – процессом определения влияния на результаты анализа одной или нескольких ключевых переменных. Анализ чувствительности рассматривается как формализованное определение серии вопросов типа "что если".

Типичные кривые NPV

Источник: T. Jensen. Network Planning – Introductory Issue. – Telektronikk, №3/4, 2003.

 

 

2 Многомерные сети — будущее инфокоммуникационных сетей.

В настоящее время в странах СНГ и, в частности, в Казахстане, сети NGN внедряются в виде отдельных, подчас весьма не похожих друг на друга, фрагментов, вкрапленных в существующие национальные сети инфокоммуникаций. Поэтому, несмотря на то, что применительно к сетям NGN разработано уже довольно много международных рекомендаций и стандартов, дискуссия, что же собой представляют инфокоммуникационные сети будущего и как их развитию должна и может способствовать отраслевая наука, не теряет свою актуальность и остроту. Тем более, что есть необходимость разрешения противоречий концепции NGN с практикой внедрения ее положений. Наряду с обсуждением сущности и путей развития сетей NGN имеет смысл заглядывать и в несколько более отдаленное будущее, когда на смену сетям NGN придут сети будущих поколений (Future Generation Networks), называемые в [4] сетями FGN XXI, а в [3] — сетями эры post-NGN. В данной лекции делается попытка хотя бы в самых общих чертах предугадать облик инфокоммуникационных сетей будущего и рассмотреть вопрос о влиянии современного представления об этих сетях на парадигму научных исследований в области телекоммуникаций [5]. Данный вопрос актуален, так как пока неясно, придут ли сети FGN на смену сетям NGN в ходе эволюции последних или в результате трудно предсказуемых революционных изменений в телекоммуникационной отрасли. Сети NGN, post-NGN эры и смена парадигмы в области инфокоммуникаций. В настоящее время бытует мнение, что смена парадигм в телекоммуникациях вообще и в проведении научных исследований в области телекоммуникаций, в частности, заключается в переходе от современных сетей к сетям NGN и в возрастании роли исследований, на правленных на повышение качества обслуживания без умаления важности решения задач технологической совместимости и гармонизации услуг [5, 6]. При научных и научно-технических революциях, согласно Т. Куну, происходит смена парадигмы, заключающаяся в том, что сущность перечисленных выше понятий меняется. Применительно к инфокоммуникациям это изменение взгляда на их облик ифункционирование своего рода смена идей [6]. Переход от сетей NGN к сетям FGN, отличающимся от сетей NGN принципами их построения. Известно, что в основу сетей NGN положен принцип «много услуг — одна сеть» и следование этому принципу будет, по всей вероятности, иметь место и в сетях FGN. В чем же тогда основное отличие развиваемых уже сейчас сетей NGN и сетей FGN, которые рано или поздно придут им на смену? Как отмечается в [7], отличие заключается в следующем. Современные инфокоммуникационные сети — это не только сети транспорта и доступа, но еще и сети поддержки и сервиса, то есть сети синхронизации, сигнализации, управления, сети передачи сигналов времени и т. п. Все они имеют собственные технические и, в частности, вычислительные средства и решают с их помощью поставленные задачи. В совокупности сети транспорта, доступа, поддержки и сервиса, разумеется, частично взаимодействуют между собой, но такое взаимодействие происходит лишь по мере необходимости и не рассматривается как существенный принцип их развития и совершенствования в условиях автономности существования этих сетей. Поэтому принцип «много услуг — одна сеть» не только в современных сетях, но и в сетях NGN в значительной степени декларативен. Иное дело — сети FGN. Предугадать их архитектуру и даже общие принципы построения затруднительно, но все же анализ тематики некоторых совре-менных теоретических исследований в области сложных систем и разнообразных сетевых структур позволяет сделать некоторые предположения о возможном облике и даже некоторых особенностях сетей будущего. Есть основание полагать, что это будут многомерные сети. К вопросам теории построения такого рода сетей в различных областях естествознания и, в том числе, в области телекоммуникаций в последние годы проявляется значительный интерес. Известно, что многомерность, рассматриваемая как конструктивный принцип, является способом объединения разрозненных сущностей в единое целое и, соответственно, многомерные сети будущего не обязательно должны иметь четко выраженное деление на сети транспорта, доступа и упомянутые сети поддержки и сервиса. Поэтому в сетях FGN, т. е. в инфокоммуникационных сетях будущего, станет возможным за счет использования многомерной структуры сети и многоядерных вычислительных средств в ее узлах обеспечивать обмен информацией и предоставление разнообразных услуг потребителям. При таком подходе доступ, транспорт, сервис, поддержка (синхронизация, сигнализация и т. д.) — это внутреннее дело интегрированной сетиFGN, многомерная архитектура которой в принципе предоставляет возможности совместного решения задач, возложенных на составляющие ее сети, в том числе неординарными способами, соответствующими уровню изобретений. Из-за этого и из-за ряда других причин, в том числе в связи с трехмерностью про странства реального мира, данного нам в ощущениях, сложнейшую гиперфигуру многомерной сети даже в самом общем виде наглядно представить невозможно. Поэтому на рис. 1 гиперфигура, отождествляемая символически с многомерной сетью будущего, представлена лишь простейшей ее проекцией, а именно — пресловутым «черным квадратом».

 

Можно предположить, что для загадочной гипотетической сети FGN самое простое решение, при котором сети доступа, транспорта и разные сети под держки находятся в своих собственных, только для них отведенных, измерениях вряд ли будет лучшим решением. Между прочим, по сути, хоть и с некоторой натяжкой, такое положение как раз имеет место сейчас, если, например, существующую сеть общего пользования можно зрительно рассматривать тоже как многомерную сеть, где в своих собственных измерениях находятся: транспорт, доступ и разные сети поддержки и сервиса [7]. Напротив, в сети FGN, при ее изначально и принципиально многомерной структуре можно будет использовать общие ресурсы этой сети и особенно ресурсы вычислительных средств различными, а, возможно, и всеми подсетями этой многомерной и, как правило, многоуровневой сети (разумеется, по изобретенным или просто придуманным, но впоследствии стандартизированным правилам). Эти возможности, а также использование на сетях многоядерных вычислительных средств с памятью, подобной многомерной памяти супер компьютеров, безусловно, будет способствовать разработке и реализации принципов построения многомерной сети с максимальным использованием ее ресурсов. В общем, повторяя приведенную в [7] цитату из Экклезиаста, с переходом к сетям FGN придет время не разбрасывать, а собирать камни, понимая под камнями все сети, входящие в объединенную многомерную сеть. Соответственно переход к многомерным сетям с максимальным использованием имеющихся у них ресурсов может рассматриваться как весьма существенный, если не главный, показатель отличия сетей FGN от современных сетей, в том числе сетей NGN. Если теперь на основании изложенного попытаться дать определение сети FGN, то можно предположить, что это будет многомерная и, как правило, многуровневая сеть, в которую интегрированы транспортная сеть, сеть синхронизации, сеть сигнализации и другие сети поддержки транспорта и доступа, а также сервисные сети для совместного наилучшим образом надежного, качественного и безопасного предоставления разнообразнейших услуг потребителям (пользователям). С приближением времени перехода от сетей NGN к сетям FGN возрастет вероятность смены современной парадигмы телекоммуникаций парадигмой создания, развития и совершенствования многомерных инфокоммуникационных сетей. Как представляется автору, эта вероятность уже сейчас отлична от нуля. И все же в настоящее время мнение о необходимости разработки, создания и исследования телекоммуникационных сетей, как интегрированных сетей с четко выраженной многомерной структурой, по крайней мере, в нашей стране и других странах, входящих в СНГ, далеко не господствующее. В связи с этим имеет смысл рассмотреть вопросы, связанные с многомерностью сетевых структур инфокоммуникаций немного подробнее. Многомерность сетевой структуры и математические основы теоретического исследования сетей NGN и FGN. Как известно из толковых словарей, термин «многомерный» означает «имеющий несколько измерений». Соответственно многомерность структуры сети означает, что сеть развивается не в двух и даже не в трех, а в N измерениях, где N больше трех (точнее, больше или равно трем, если трехмерность тоже понимать как многомерность). При N > 3 в связи с тем, что память многомерна пока еще не у всех компьютеров, необходимо тем или иным образом осуществлять соответствующее N-мерное представление как исходных, так и обрабатываемых данных. Математической основой такого представления могут служить давно известные в фундаментальной математике многомерные матрицы [8], а в вычислительной технике — многомерные массивы. Уместно вспомнить, что, например, Г. Крон предложил использовать многомерные матрицы при тензорном анализе электротехнических цепей еще в 30-е годы прошлого века. С помощью мно-гомерных матриц и соответствующих массивов данных, (методам обработки которых посвящено много публикаций [9]), многомерное представление тех или иных сущностей вполне практически осуществимо. Примеры этому можно найти также в публикациях, посвященных многомерному представлению сетей синхронизации [10, 11] и подобному же их представлению совместно с транспортными телекоммуникационными сетями. Известно также, что существуют результаты абстрактного теоретического исследования многомерно-матричных сетей применительно к любым сетям (социальным, нейронным, транспортным в любом смысле и т. д.) [12, 13]. Наличие подобной литературы и довольно давняя история многомерного представления разных сетей не мешает, однако, изобретателям запатентовывать новые идеи, имеющие прямое отношение к многомерным компьютерным и телекоммуникационным структурам. Типичными в этом отношении являются патенты, в описании к которым изложены предложенные изобретателями конкретные принципы построения определенных многомерных структур. Подобные изобретения представляют особый интерес, так как они дают возможность, помимо общего представления о многомерной сетевой структуре, понять возможности совершенствования сетей с использованием особенностей такого рода структур. Одна из общих характеристик некоторых возможностей, показано на рис. 2, где в чрезвычайно упрощенном виде приведен пример многомерной структуры сети, состоящей из трех подсетей при очень ограниченном числе сетевых элементов (СЭ), относящихся в этой сети к определенным иерархическим уровням (Hierarchical levels).

Рисунок 2. Многомерная структура сети

Отметим, что эти иерархические уровни не следует отождествлять с упомянутыми ранее уровнями (Layers) эталонной модели взаимодействия открытых систем. Чтобы не загромождать рисунок, на нем представлены лишь взаимосвязи СЭ, которые имеют место при передаче информации из пунктов А, B и C первого иерархического уровня в конечный пункт К третьего иерархического уровня и только в одном направлении. В примере, представленном на рис. 2, где подсети рассматриваемой сети разделены на иерархические уровни, нумерация СЭ произведена с учетом этого обстоятельства. В результате сетевые элементы, кроме того, что они перенумерованы по порядку (порядковые номера показаны вверху эллипсов, обозначающих СЭ), характеризуются также порядковым номером на соответствующем иерархическом уровне, номером этого уровня и номером подсети (эти номера последовательно приведены чуть ниже эллипсов, символизирующих СЭ). Связность сетевых элементов сети, представленной ориентированным графом (орграфом) на рис. 2, описывается шестимерной матрицей. Она представлена на рис. 2 слева одним из своих двухмерных сечений. Использование многомерной матрицы позволяет в рассматриваемом случае для каждой подсети и для каждого уровня в конкретной подсети иметь собственные индексы. Поэтому, например, взаимосвязь 4-го СЭ на 1-м уровне 1-й подсети с 3-м СЭ на 2-м уровне этой же подсети отображается элементом S 4,3,1,2,1,1 в представленном на рис. 2 сечении матрицы S <N>, где N = 6 — число ее измерений. У каждого элемента матрицы S <N> первая пара индексов относится к номерам СЭ, вторая пара — к уровням, на которых эти СЭ находятся, и третья пара — к номерам подсетей. В показанном двухмерном сечении матрицы S <6> на рис. 2 только элемент S 4,3,1,2,1,1 является ненулевым, что соответствует графу, представленному на этом же рисунке справа. На рис. 2 прописными латинскими буквами обозначены пункты размещения СЭ подсетей. Предполагается, что сетевые элементы, обозначенные одной буквой, расположены вместе в одном узле интегрированной сети, причем с точки зрения передачи информации из узла в узел не имеет значения, как осуществлена маршрутизация этой передачи: в одной или разных подсетях рассматриваемой сети. Например, в сети с пакетной передачей передача пакетов из пунктов А, B и C в конечный пункт допускает образование маршрутов прохождения пакетов не в одной, а во всех трех подсетях, как это показано на рис. 2. Так, например, пакеты, направляемые в пункт К из пунктов В и С (их маршрут показан соответственно пунктирными и штрихпунктирными линиями) не создают препятствий пакетам, посланным из пункта А (сплошная линия). Это происходит потому, что они направляются в другие подсети и передаются далее к конечному пункту К с использованием избыточных ресурсов — в данном случае, второй и третьей подсетей. Это приводит к уменьшению вероятности создания различными пакетами препятствий и помех друг другу, что дает возможность таким образом уменьшить величину задержки при доставке пакетов к конечной цели. Аналогично, в сети с коммутацией каналов образование каналов передачи в разных подсетях, при определенных условиях тоже может оказаться полезным, как это можно себе представить, используя в качестве иллюстрации тот же рис. 2, приняв на этом рисунке сплошную, пунктирную и штрихпунктирную ломаные линии за

 

 

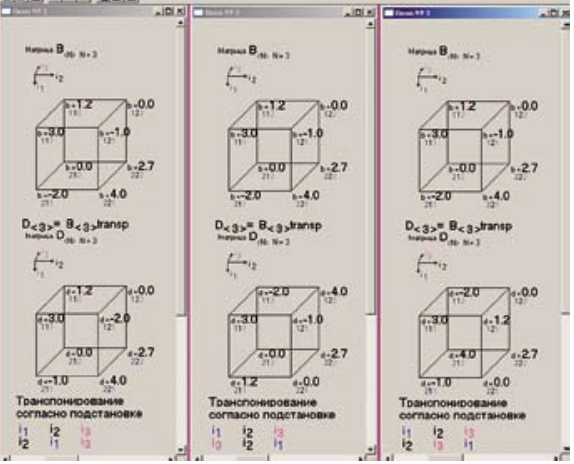
Рис. 3

маршруты каналов передачи информации в многомерной сети. Процессы, связанные с передачей информации в многомерной интегрированной сети, конечно, многократно сложнее, чем в рассмотренном крайне упрощенном примере. Кроме того, представить себе детально будущие способы совершенствования такого рода сети за счет совместного использования ее ресурсов пока затруднительно даже на основе изобретений по данной тематике. К тому же рис. 2, позволяя получить некоторое представление о взаимосвязях СЭ в рассматриваемой интегрированной сети с помощью многомерной матрицы и ее сечений, в отношении иллюстрации возможности совместного использования ресурсов многомерной сети не очень отличается от показанного на рис. 1 «черного квадрата», символизирующего недостаточную изученность путей решения этой задачи. Тем не менее, уже сейчас есть понимание того, что для использования потенциальных возможностей многомерной интегрированной сети понадобятся адекватные методы исследования и поиска наилучших решений, не ставшие еще традиционными. Некоторые из них перечислены справа в упрощенной таблице. Для сравнения там же слева перечислены методы, широко используемые сейчас в исследовании современных сетей и сетей NGN. Обратим внимание, что математические методы исследования сетей FGN представляют собой не что иное, как обобщение на N-мерный случай математического аппарата исследования современных сетей

и сетей NGN. Примером этому является алгебра многомерных (пространственных) матриц. Расширенные возможности данного математического аппарата иллюстрируются простейшими примерами на рис. 3 и 4. На первом в соответствующих окнах показано умножение пространственной трехмерной матрицы на двухмерную матрицу по разным индексам, а на втором — транспонирование подобной же трехмерной матрицы

согласно различным подстановкам индексов. Как отмечалось, методы алгебры

многомерных матриц в фундаментальной математике разработаны давно [8] и

продолжают развиваться современными математиками. Однако в телекоммуникациях их применение еще не стало традиционным. Подобное же утверждение справедливо и по отношению к остальным математическим методам, перечисленным справа в упрощенной таблице, хотя известны работы, где эти методы уже сейчас используются при исследовании вопросов, имеющих отношение к телекоммуникационным сетям. Можно

надеяться, что более широкое использование математических методов, перечисленных в таблице, будет способствовать приближению post-NGN эры, знаменующей переход к сетям FGN. Обратим внимание также на то, что при организации и проведении поисковых работ по определению принципов создания и нахождению инженерных решений построения многомерных сетей FGN существенное значение могут иметь новые элементы интенсивно развиваемых в настоящее время теорий многомерных многоуровневых сетей, образуемых (в том числе виртуально) в различных областях человеческой деятельности. Многие работы по этой тематике, подобные упомянутым, но в меньшей степени относящиеся к телекоммуникациям, остались вне приведенного ниже списка литературы, который за счет такого рода работ мог бы быть существенно расширен. Чтобы убедиться в этом, достаточно предпринять поиск словосочетаний «многомерные сети» и «multidimensional networks» в Интернете. С другой стороны, нельзя игнорировать то, что подход, связанный с рассмотрением сетей FGN как соответствующим образом структурированных многомерных сетей, открывая определенные заманчивые перспективы их совершенствования, одновременно связан с необходимостью преодоления существенных трудностей. К их числу относится, например, то обстоятельство, что фундаментальная математическая основа теории гиперсетей, и тем более связанные с ней вычислительные методы, алгоритмы и программное обеспечение заметно сложнее тех, которые считаются традиционными, как, например, методы, базирующиеся на математическом

аппарате обычных матриц и теории графов [14]. Соответственно разработка технических средств многомерной сети и ее программного обеспечения

вряд ли станет менее трудоемкой и затратной.

 

 

Алгебра матриц Алгебра многомерных (пространственных) матриц

При движении вперед к сетям будущего с этим придется считаться. Не исключено, что в процессе конструирования сетей FGN, для решения наибо-

лее сложных задач потребуется объединение совместных усилий специалистов отраслевой, университетской и академической науки. Такое сотрудничество может потребоваться, например, при разработке архитектурных функциональных моделей (АФМ) многомерных сетей FGN с учетом опыта разработки АФМ существующих телекоммуника-

ционных сетей [15]. Виртуальное моделирование технических решений многомерных сетей и модельные сети. В связи с изложенным выше ясно, что прогресс в разработке основ и принципов создания сетей FGN с учетом возможностей и особенностей их многомерной многоуровневой структуры неразрывно связан не только с освоением достижений в упомянутых областях фундаментальной математики, но и с разработкой нового программного обеспечения, предназначенного для исследования и проектирования такого рода гиперсетей. Кроме того, при разработке и проверке технических решений желательно шире использовать возможности современных компьютеров для создания соответствующих виртуальных, в том числе многомерно-матричных, компьютерных моделей [12]. Еще большее значение может иметь исследование перспективных технических решений, в том числе тех из них, которые способствовали бы созданию в будущем сетей FGN, с помощью мо- дельных сетей научно-исследовательских центров, подобных Международному исследовательскому центру по внедрению и тестированию новых технологий, упоминаемому в [5]. Всесторонние исследования, которые можно осуществлять с помощью такого рода модельных сетей, позволят отечественным специалистам внести свой вклад, наряду с совершенствованием развиваемых сейчас сетей NGN, в разработку принципов и технических решений интегрированных многомерных сетей,

рассматриваемых выше в качестве сетей FGN. Заключение Изложенные соображения вселяют надежду, что в будущем, причем не очень отдаленном, принципы построения многомерных сетей FGN будут разработаны, внедрены и стандартизированы в условиях стремительного развития инфокоммуникационных технологий.

 

Рис. 4

 

Литература

1 Васильев А.В., Соловьев С.П., Кучерявый А.Е. Системно-сетевые решения

по внедрению технологии NGN на российских сетях связи // Электросвязь —

2005. — № 3.

2 Кучерявый А.Е., Цуприков А.Л. Сети связи следующего поколения / М.:

ЦНИИС. — 2006.

3 Гольдштейн А., Соколов Н. На пути к Next Generation Networks. Сколько ша-

гов осталось пройти к сети будущего? //

4 Мир связи. Connect. — 2006. — № 11.

5 Варакин Л.Е. Будущее поколение инфокоммуникационных сетей — FGN

XXI // Международная конференция MAC-2004 “Инфокоммуникационные сети XXI века” — М. http://niits.ru/ public/2004/2004-039.pdf

6 Аджемов А.С. Новая парадигма научных исследований в телекоммуникаци-

ях // Электросвязь — 2006. — № 4.

7 Мардер Н.С. Смена парадигмы телекоммуникаций и семиуровневая мо-

дель взаимодействия открытых систем // Электросвязь — 2007. — № 2.

8 Коновалов Г.В. Многомерные сети как философия сетей FGN // Материалы VII международной научно-технической конференции «Перспективные технологии в средствах передачи информации — ПТСПИ’2007». 10—12 октября 2007. — Владимир: изд-во ВООО ВОИ. — 2007.

9 Соколов Н.П. Пространственные матрицы и их приложения / М.: Физмат-

гиз, 1960.

10 Муха В.С. Анализ многомерных данных / Минск.: Технопринт, 2004.

11 Коновалов Г.В. Многомерные матрицы — математический аппарат моделирования процессов конфигурации и реконфигурации // Труды МАС. —

2002. — № 1(21).

12 Коновалов Г.В. Пространственные представления структур сетей синхронизации и их описание с помощью многомерных матриц // Метрология

и измерительная техника в связи. — 2004. — № 6.

13 Коновалов Г.В. Создание виртуальных многомерно-матричных моделей сигнальных, сетевых и сигнально-сетевых структур в качестве средства для исследования материальных объектов мира информационной реальности // Сборник «XIII Международная научнотехническая конференция «Радиолокация, навигация, связь». Том 1. 17—19 апреля 2007. Воронеж: изд-во ВГУ, 2007.

14 Gasparyan A.S. Multidimensional Matrix Networks: a New Approach to Modelling Social Networks. Abstracts // International Social Network Conference. SUNBELT, XXIII Cancun, Quantana Rao, Mexico, February 11, 2003.

15 Вишневский В.М. Теоретические основы проектирования компьютерных сетей / М.: Техносфера, 2003.

16 Калмыков В.В., Меккель А.М., Соколов Н.А., Шинаков Ю.С. Транспорт и