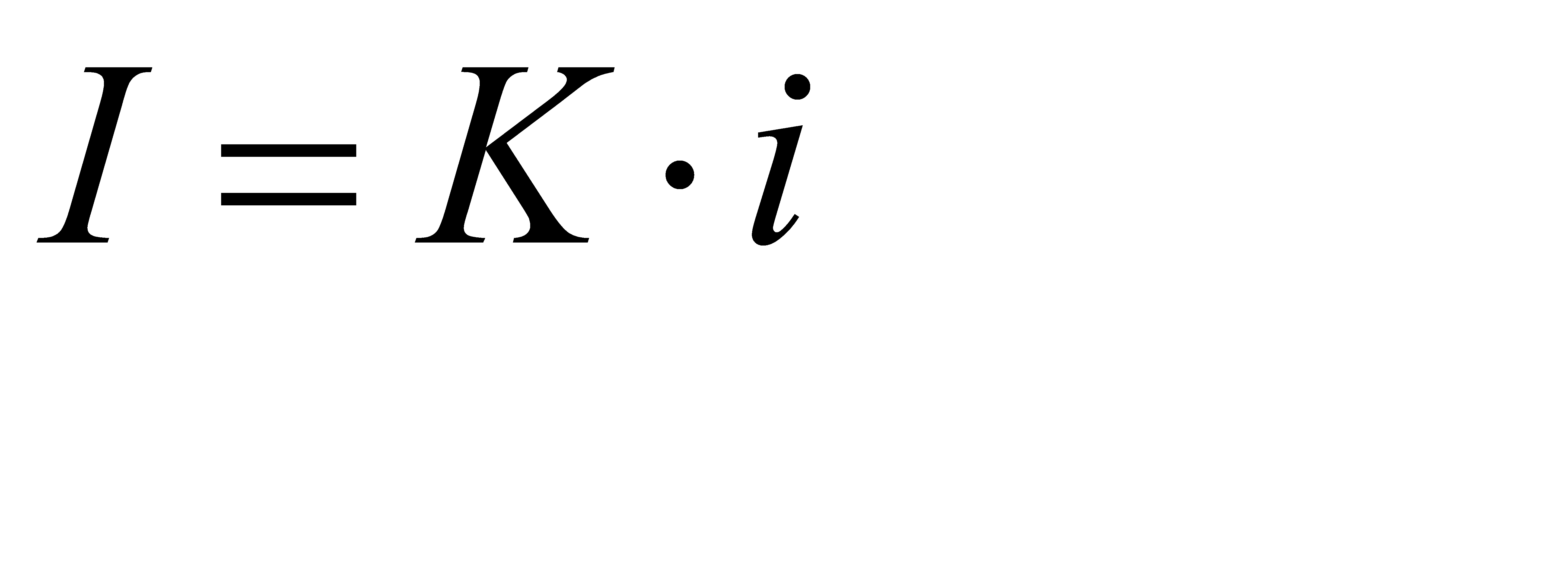Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алфавитный подход к измерению количества информацииСодержание книги
Поиск на нашем сайте
Алфавит – м ножество символов, используемых при записи текста. Полное количество символов в алфавите называется размером (мощностью) алфавита. Алфавитный подход позволяет определить количество информации в тексте. Данный подход является объективным, т.е. он не зависит от человека, воспринимающего текст. Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то мощность (N) алфавита вычисляется по формуле:
где i – информационный вес одного символа в используемом алфавите. Если весь текст состоит из К символов, то при алфавитном подходе размер содержащейся в нем информации равен:
Вопрос 4: Системы счисления Под системой счисления понимается определенный способ записи числа с помощью некоторого алфавита символов a1, a2,…, an. При этом каждой цифре ai в записи числа ставится в соответствие определенное количественное значение.
Количество цифр, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления (S). Любое число A в позиционной системе счисления может быть представлено в виде суммы коэффициентов ai из алфавита данной системы умноженных на степени основания S системы счисления: AS=anan-1an-2…a2a1a0,a-1a-2…a-m= =an*Sn + an-1*Sn-1 + an-2*Sn-2 + …a2*S2 + a1*S1 + a0*S0 +a-1*S-1 + a-2*S-2 + … + a-m*S-m. Таблица 1 Алфавит основных систем счисления
В математике для записи числа используется десятичная система счисления (S=10), ее алфавит состоит из десяти арабских цифр 0, 1, 2,…, 9. Любое число в этой системе счисления можно представить следующим образом: A10=an*10n + a1*101 + a0*100+a-1*10-1 … + a-m*10-m. Например, 32,1910=3·101+2·100+1·10-1+9·10-2. В аппаратной основе вычислительной техники для физического представления чисел, предназначенных для обработки, используются двухпозиционные элементы, которые могут находиться только в одном из устойчивых состояний. Одно из этих состояний обозначает цифру 0, а другое – цифру 1. Поэтому наибольшее распространение в ЭВМ получила двоичная система счисления, основание которой S=2. Ее алфавит состоит из двух цифр 0 и 1. Например, двоичное число 10011,01=1·24+0·23+0·22+1·21+1·20+0·2-1+1·2-2=16+2+1+0,25=19,2510 соответствует десятичному числу 19,2510. Таблица 2 Правила двоичного сложения, вычитания и умножения
Для более компактной записи чисел обычно используются восьмеричная и шестнадцатеричная системы счисления. Поэтому большое практическое значение имеют процедуры перевода из одной системы счисления в другую.
В восьмеричной системе счисления (S=8) используется восемь цифр 0,1,…,7. Например, переведем число из восьмеричной системы счисления 237,48 в десятеричную систему счисления 237,48=2·82 + 3·81 + 7·80 + 4·8-1 = 128+24+7+0,5=159,510. Переведем число из десятичной системы счисления 75,5910 в восьмеричную систему счисления Остаток 75:8 = 9 (3) 9:8 = 1 (1) 1:8 = 0 (1)
0,59·8 = 4,72; 0,72·8 = 5,76; 0,76·8 = 6,08, … Таким образом, 75,5910 = 113,4568
В шестнадцатеричной системе счисления алфавит состоит из 16 цифр, где первые десять символов обозначаются цифрами от 0 до 9, а далее используются буквенные обозначения: 10 – A, 11 – B, 12 – C, 13 – D, 14 – E, 15 – F. Предложенный алфавит позволяет записать все десятичные цифры от 0 до 15, остальные цифры представляются следующим образом:
Остаток Остаток Остаток 16:16 = 1 (0) 17:16 = 1 (1) 18:16 = 1 (2) 1:16 = 0 (1) 1:16 = 1 (1) 1:16 = 0 (1)
1610=1016 = 1·161+0·160; 1710=1116 = 1·161+1·160; 1810=1216 = 1·161+2·160.
Существует также способ взаимного перевода чисел из восьмеричной и шестнадцатеричной системы счисления в двоичную систему счисления, благодаря использованию таблицы соответствия чисел в двоичной, восьмеричной и шестнадцатеричной системах счисления (Табл.3). Таблица 3 Соответствие чисел в двоичной, восьмеричной и шестнадцатеричной системах счисления
Например, переведем число 162,378 из восьмеричной системы счисления в двоичную и шестнадцатеричную системы счисления 162,378 = 001110010, 011111 2, 1 6 2 3 7 01110010, 01111100 2 = 72,7C16 7 2 7 C Получаем, 162,378 = 1110010,0111112 = 72,7C16
Для выполнения арифметических операций над числами в ЭВМ используют специальные машинные коды: прямой, обратный и дополнительный. Применение машинных кодов сводит операцию вычитания к алгебраическому суммированию кодов этих чисел, упрощается определение знака результата операции. В данных машинных кодах перед старшим цифровым разрядом располагается знаковый разряд, в котором записывается нуль для положительного числа и единица для отрицательного числа. В дальнейшем при написании машинных кодов будем отделять знаковый разряд от цифровых разрядов точкой. Прямой код двоичного числа содержит цифровые разряды, перед которыми записан знаковый разряд. Прямой код используется для представления отрицательных чисел в запоминающем устройстве ЭВМ. Например, для двоичных чисел x = +10102 и y = -11012 их прямые коды будут иметь следующий вид: xпр = 0.10102 и yпр = 1.11012. Обратный код положительного числа полностью совпадает с его прямым кодом. Для отрицательного числа он содержит единицу в знаковом разряде, а значащие цифровые разряды числа заменяются на инверсные, то есть единицы заменяются нулями, а нули – единицами. Таким образом, для приведенного выше примера имеем: xобр = xпр = 0.10102 и yобр = 1.00102. Дополнительный код положительного числа полностью совпадает с прямым кодом, а следовательно и с обратным. Для отрицательного числа он образуется из обратного путем прибавления к нему единицы к младшему цифровому разряду. Следовательно, получаем: xдоп = xобр = xпр = 0.10102 и yдоп = 1.00112.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.21.237 (0.006 с.) |