
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математика: экономико-математические методыСодержание книги
Поиск на нашем сайте ЗАДАЧИ И УПРАЖНЕНИЯ ПО КУРСУ МАТЕМАТИКА: ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ ЧАСТЬ 1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ (ЛП) Составить двойственные задачи к следующим задачам ЛП.
Составить двойственные задачи к следующим задачам ЛП и найти решение каждой пары геометрическим методом.
9. Проверить, является ли точка x/= (1/2, 0, 0)оптимальным планом задачи ЛП. f(x) = 2x1+6x2+4x3 0,2x1 + x2 + 2x3 ≤ 1, x1 + 2x2 + x3 x1, x2, x3
10. Проверить, есть ли среди точек x / = (5, 0, 0, –2), x // = (1, 1/2, 1/2, 0), x /// = (2, 1, 0, 0) оптимальный план задачи f(x) = 4 x1+ 3 x2 – 3 x3 – 2x4 x1+ x2 + 3 x3+ x4 = 3 x1– x2 + x3 + 2 x4 = 1 xj Найти решение следующих задач ЛП, используя условия равновесия. В ответе указать оптимальные планы прямой и двойственной задач и значения целевых функций.
Найти решение следующих задач ЛП, используя условия равновесия, если известно оптимальное решение двойственной задачи (геометрически решать не надо!).
Проверить с помощью условий равновесия, является ли точка x/ оптимальным планом задачи (геометрически решать не надо!).
19. Фабрика производит три типа изделий А, В, С, используя для этого два вида сырья S1 и S2. Расход сырья на одно изделие, его запасы и цена реализации единицы продукции приведены в таблице
Найти план выпуска продукции, максимизирующий суммарный доход. 20. По предписанию врача пациенту необходимо перейти на витаминную диету и за сезон употребить витамина В1 и витамина В2, содержащихся во фруктах, в количествах не менее, чем указано в таблице:
Определить, какое количество фруктов каждого вида необходимо купить за сезон, чтобы выполнить предписание врача с минимальными расходами.
ТЕМА 3. СИМПЛЕКС–МЕТОД Найти все базисные планы канонической задачи ЛП. Построить множество планов эквивалентной задачи ЛП с двумя переменными и указать на нем угловые точки, соответствующие базисным планам.
Нелинейное программирование (НЛП) Тема 1. Геометрическое решение задач НЛП На заданном множестве Х найти экстремумы заданных функций f(x).
a) b) c) 2. X: a) 3. X: b) 4. X: 5. X: 6. X: 7. X: ЗАДАЧИ И УПРАЖНЕНИЯ ПО КУРСУ МАТЕМАТИКА: ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 max,
max,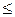 2,
2, 0.
0.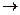 max
max 0, j =1,2,3,4
0, j =1,2,3,4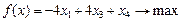
 ,
,
 ,
,


 ,
,
 ,
,

 ,
,
 ,
,


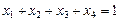

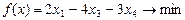
 ,
,
 ,
,


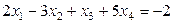 ,
,
 ,
,

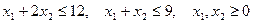 .
.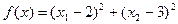 ,
,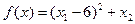 ,
, .
.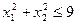 ,
, 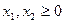 .
. , b)
, b) 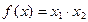 .
. . a)
. a)  ,
,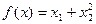 ,
,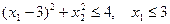 .
. 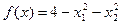 .
. ,
, 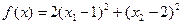 .
.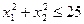 ,
, 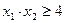 ,
, 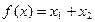 .
.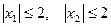 .
. 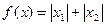 .
.


