Математическая постановка задачи

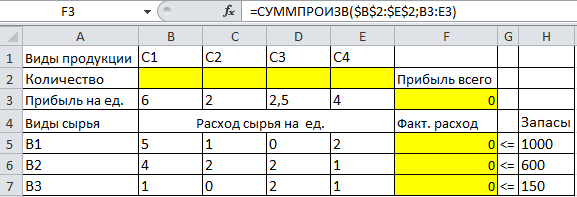
Обозначим через Х1, Х2, Х3 и Х4 количество единиц соответствующих изделиям С1, С2, С3 и С4. Математическая модель задачи будет иметь следующий вид: найти максимум функции У=6 Х1 + 2Х2 + 2,5Х3 + 4Х4

при выполнении ограничений:

5Х1 + Х2 + 2 Х4 <= 1000

4Х1 + 2Х2 + 2Х3 + Х4<= 600

Х1 + 2Х3 + Х4 <= 150

Х1>= 0, Х2 >= 0, Х3 >= 0, Х4 >= 0,

Методические указания

1. Оформите исходную таблицу:

2. Ячейку F3 введите формулу =СУММПРОИЗВ($B$2:$E$2;B3:E3).Скопируйте формулу в ячейки F5:F7.

3. Выделите оптимизируемую ячейку F3. На вкладке Данные щелкните по кнопке Поиск решения. В окне диалога Поиск решения в поле Установить целевую ячейку уже находится ссылка на выделенную ячейку. При необходимости эту ссылку можно изменить.

4. Укажите, что хотите максимизировать значение целевой ячейки.

5. Перейдите в поле Изменяя ячейки. Изменяемая ячейка – это ячейка, которая может быть изменена в процессе Поиска решения для достижения нужного результата. В данном примере это ячейки В2:Е2 – количество изделий.

6. Нажмите кнопку Добавить, чтобы ввести Ограничения.

7. В окне Добавления ограничения введите первое ограничение: значения в ячейках В2:Е2 должны быть больше нуля. Для этого:

- В поле Ссылка на ячейку укажите ячейки В2:Е2.

- Нажмите клавишу TAB для перехода в следующее поле.

- Выберите Оператор >=.

- В поле Ограничение введите 0.

8. Нажмите кнопку Добавить, чтобы ввести следующее ограничение: F5:F7<= H5:H7 (расход ресурсов не должен превышать их наличие). После ввода ограничения нажмите ОК.

9. Нажмите кнопку Выполнить. По окончании поиска решения появится диалоговое окно результатов. Выберите переключатель Сохранить найденное решение. Нажмите ОК.

10. Сделайте вывод по результатам решения.

Задание 2. Оптимизация плана производства

Фирма «ТЕХНОМИР» хочет разработать план сборки компьютеров. Спрос на компьютеры прогнозируется: в первом квартале – 1000, во втором – 500, в третьем – 3000 и в четвертом – 2000 штук.

При работе в одну смену фирма может собрать 1200 компьютеров каждый квартал при стоимости сборки одного компьютера 100 рублей. Если ввести вторую смену, то ежеквартально можно собирать еще 800 компьютеров, но сборка каждого компьютера во вторую смену обходится дороже – 110 руб. Изготовленные в данном квартале компьютеры могут продаваться в одном из последующих кварталов. При этом хранение каждого компьютера обходится в 25 рублей за квартал.

Определите, сколько компьютеров нужно собирать ежеквартально в первую и во вторую смены, чтобы удовлетворить спрос с минимальными совокупными затратами.

Методические указания

Оформите в EXCEL таблицу (см. ниже) и введите в ячейки следующие зависимости:

С3=СУММ(D3:G3); C4=СУММ(D4:G4); C5=СУММ(E5:G5)

C6=СУММ(E6:G6); C7=СУММ(F7:G7); C8=СУММ(F8:G8); С9=G9

C10=G10; С11=СУММ(D11:G11); D11=СУММ(D3:D4)

E11=СУММ(E3:E6); F11= СУММ(F3:F8); G11= СУММ(G3:G10)

C22= СУММ(D22:G22); D22=СУММПРОИЗВ(D3:D4;D14:D15)

E22= СУММПРОИЗВ(E3:E6;E14:E17); F22= СУММПРОИЗВ(F3:F8;F14:F19)

G22= СУММПРОИЗВ(G3:G10;G14:G21)

	А	B	C	D	E	F	G
	Производство	Реализация
	1 кв	2 кв	3 кв	4 кв
	1 кв	1 см
	2 см
	2 кв	1 см
	2 см
	3 кв	1 см
	2 см
	4 кв	1 см
	2 см
	Всего
	Спрос
	Мощности	Издержки на производство и хранение
	1 кв	1 см
	2 см
	2 кв	1 см
	2 см
	3 кв	1 см
	2 см
	4 кв	1 см
	2 см
	Затраты

 

 

В диалоговом окне Поиск решения задайте следующие параметры:

Параметры задачи	Ячейки	Описание
Целевая ячейка	С22	Цель – снижение издержек на производство и хранение.
Изменяемые данные	D3:G10	Реализация компьютеров по сменам и кварталам.
Ограничения	С3:C10<= C14:C21	Производство не может превышать имеющиеся мощности.
D11:G11>= D12:G12	Реализация не должна быть меньше спроса на продукцию.
D3:G10>=0	Неотрицательность переменных.

Задание 3

Городской молочный завод производит молочные продукты трех видов: молоко, кефир, сметана. Определить оптимальный ассортимент, обеспечивающий максимум прибыли.

Завод должен ежедневно производить не менее 100 т молока и 10 т кефира.

На производство 1 т молока, кефира и сметаны расходуется соответственно 1,01; 1,01; 9,45 т молока-сырья. Наличие сырья составляет 136 т.

Затраты рабочего времени при разливе 1 т молока и кефира составляют 0,18 и 0,19 маш.-час. На расфасовке 1 т сметаны используются специальные автоматы в течение 3,25 час. Основное оборудование может быть занято в течение 21,4 маш.-час., а автоматы по расфасовке сметаны – в течение 16,25 час.