
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа 2. Определение концентрацииСодержание книги Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ «ГОРНЫЙ»
Кафедра общей и технической физики
Общая физика ВОЛНОВАЯ ОПТИКА
Поляризация световых волн. Искусственная оптическая анизотропия
Лабораторный практикум
САНКТ-ПЕТЕРБУРГ УДК 535.41/42 + 535.5 (075.80) ББК 22.34
Общая физика. ВОЛНОВАЯ ОПТИКА. Поляризация световых волн. Искусственная оптическая анизотропия: Лабораторный практикум / А.С.Мустафаев, С.В. Егоров. Национальный минерально-сырьевой университет «Горный». СПб, 2012. 38 с. ISBN 5-94211-162-6
В лабораторном практикуме представлены работы по всем основным оптическим явлениям: дисперсии, поляризации, поглощению света, искусственной оптической анизотропии, вызываемой электромагнитными полями, и вращению плоскости поляризации. Практикум предоставляет возможность студентам познакомиться с явлениями, лежащими в основе современных оптических технологий. Основная задача - овладеть техникой и методикой проведения экспериментальных исследований, а также приемами обработки результатов исследований и оформления заключительного отчета. В зачетных работах практикума, выполняемых по индивидуальной программе, студент должен продемонстрировать умение в устной и письменной форме, логически верно, и аргументировано защищать результаты своих исследований. Лабораторный практикум предназначен для студентов, бакалавров и магистров всех специальностей и форм обучения Санкт-Петербургского государственного горного университета.
В постановке работ № 3, 4 и оформлении лабораторного практикума принимали участие ассистенты профессора, студенты группы ИЗ-09-3: Апалонов Иван, Горюнова Лолита.
Научный редактор проф. А.С. Мустафаев
ПОЛЯРИЗАЦИЯ СВЕТОВЫХ ВОЛН
Работа 1. ИССЛЕДОВАНИЕ ПОЛЯРИЗОВАННОГО СВЕТА
Теоретические сведения
Видимый свет, как известно, представляет собой электромагнитные волны с длинами волн от 4×10–7 м (фиолетовый) до 7×10–7 м (красный). В электромагнитной волне векторы напряженности электрического поля Для полной характеристики волны задают ее длину l, модули векторов
Естественный или неполяризованный свет можно рассматривать как наложение многих электромагнитных волн, распространяющихся в одном и том же направлении, но со всевозможными ориентациями плоскостей колебаний. Таким образом, для неполяризованного света нельзя указать даже плоскость преимущественного расположения вектора напряженности электрического поля Если в световом пучке вектор Если составляющие вектора · естественный или неполяризованный свет; · частично поляризованный свет; · линейно или плоско поляризованный свет; · свет, поляризованный по кругу; · эллиптически поляризованный свет.
Пусть на поляризатор падает плоскополяризованное излучение интенсивностью I 0 (рис.2). Разложим вектор I ~ < E ||2 > = < E 02 cos2j >, здесь угловые скобки обозначают, усреднение по времени. Учитывая, что интенсивность падающего излучения I 0~ < E 02>, получим I = I 0cos2j. (1) Последнее соотношение называют законом Малюса. Если направить на поляризатор естественное (неполяризованное) излучение, в котором все ориентации вектора напряженности равновероятны (т.е. возможны любые значения j), то проводя усреднение по углу j в соотношении (1) получим I = 0,5 I ест. Таким образом, при прохождении через поляризатор естественное излучение становится линейно-поляризованным, но убывает по интенсивности вдвое. Для количественной оценки степени поляризацииизлучения применяется соотношение
Частично поляризованное излучение понимается как смесь линейно поляризованного и неполяризованного излучений. Тогда I – полная интенсивность, I п – интенсивность линейно-поляризованного компонента. Очевидно, Если направить частично поляризованное излучение на поляризатор и вращать устройство, меняя угол между главной плоскостью поляризатора и преимущественным направлением вектора I max = I п + I н / 2. (3) Во втором положении, которое отличается по углу от первого на 90°, поляризованный компонент, согласно закону Малюса, полностью задерживается, а неполяризованный по-прежнему уменьшается вдвое: I min = I н/ 2. (4) Складывая и вычитая уравнения (3) и (4), имеем Р = (I max – I min) / (I max + I min). (5) Способ получения эллиптически поляризованного излучения. Допустим, что из двоякопреломляющего кристалла вырезана пластинка таким образом, что оптическая ось лежит в плоскости среза. Допустим далее, что излучение падает на пластинку перпендикулярно плоскости среза. В этом случае колебания электрического вектора, как в обыкновенной волне ( Направления электрических векторов обыкновенного и необыкновенного лучей взаимноперпендикулярны. И эти лучи распространяются в одном направлении, но с разными скоростями. В связи с этим, при прохождении через пластинку между ними возникает разность хода: D L = (n o – n e) d, (6) где d – толщина кристаллической пластинки; n o и n e показатели преломления обыкновенного и необыкновенного лучей. Как уже отмечалось, при наличии разности хода волны могут интерферировать только в том случае, если они когерентны. Если падающее на кристалл излучение не поляризовано, о - и е -волны испускаются разными группами атомов (не согласованно), поэтому волны не когерентны. Если же на кристалл падает линейно-поляризованный свет, то волна разделяется между о- и е-волнами в пропорции, которая зависит от ориентации плоскости колебаний. Поэтому возникающие о- и е-компоненты когерентны и способны интерферировать.
Из теории сложения колебаний известно, что при сложении взаимно перпендикулярных колебаний одинаковой частоты конец результирующего вектора x 2/ E о2 – (2 xy / E о E е) cos (dj) + y 2/ E е2 = sin2(dj), где dj – сдвиг фаз колебаний на выходе из пластинки кристалла; x и y – координаты конца результирующего вектора Нас интересует случай, когда эллипс ориентирован своими полуосями по осям Оx и Оy (Оу лежит в главной плоскости кристалла), при этом E oи E eявляются полуосями эллипса. Это наблюдается, если выполнено условие для разности фаз: Ex 2/ E о2 + Ey 2/ E e2 = 1. Разность фаз колебаний связана с разностью хода лучей: dj = d (n o – n e) = ±(λ0/4 + k λ). (7) Здесь знак плюс соответствует отрицательным кристаллам (n o> n e), знак минус – положительным кристаллам (n o < n e). Таким образом, если толщина пластины, вырезанной вдоль оптической оси, удовлетворяет условию (7), результатом будет эллиптическая поляризация выходящего излучения. Такая пластина носит название четвертьволновой или пластины λ/4. Способ полученияциркулярной (круговой) поляризации излучения. Эллипс превращается в окружность при равенстве полуосей эллипса, т.е. E o = Ee º E. Этого достигают, ориентируя четвертьволновую пластину оптической осью под углом a = 45° к плоскости колебаний падающего излучения. При этом компоненты результирующего вектора
Описание экспериментальной установки
Излучение полупроводникового лазера 1 (рис.4) близко к линейно-поляризованному. В первом случае (без четвертьволновой пластинки 2) оно направляется на анализатор 3 и затем попадает на фотодетектор 4. Фототок, пропорциональный интенсивности света, прошедшего через анализатор, измеряется микроамперметром 5, включенным в режиме измерения тока. Полупроводниковый лазер находится в цилиндрическом кожухе, укрепленном на стойке. Анализатор 3 укреплен в поворотном элементе со шкалой отсчета угла в градусах и зубчатым колесом, облегчающим вращение. Четвертьволновая пластина 2 смонтирована в круглой вращающейся оправе, на которой по ободу нанесена шкала для измерения угла поворота. Переключатель режимов работы микроамперметра (шунт) до начала и после окончания измерений должен находиться в положении «¥». В этом случае прибор отключен и можно проверить нулевое положение светового указателя микроамперметра. Затем шунт переключают в положение, при котором регистрируется сигнал (положение «1 мкА» или «5 мкА») и проводят измерения.
Порядок выполнения работы
Задание 1. Исследование степени поляризации лазерного излечения. Излучение лазера линейно поляризовано. В этом необходимо убедится. Для этого: 1. Проверить установку в соответствии со схемой. На оптической скамье установить лазер, анализатор и фотодетектор, сняв с оптической скамьи четвертьволновую пластинку. 2. Поворачивая анализатор вокруг горизонтальной оси, наблюдать за табло измерительного прибора. Если фототок, регистрируемый прибором, при вращении анализатора изменяется от нуля до некоторого максимального значения, то это, означает, что излучение линейно поляризовано. Результаты измерений фототока в зависимости от поворота анализатора записать в таблицу 1. Таблица 1
3. По полученным экспериментальным данным построить лепестковую диаграмму
Задание 2. Изучение закона Малюса. 1. «Ноль» на шкале поворотного элемента, в котором закреплён анализатор, не совмещен с положением оптической оси анализатора. Поэтому, согласно закону Малюса, следует принять за «0о» значение экспериментального угла поворота, при котором фототок максимален I0. 2. Затем вновь поворачивая анализатор вокруг горизонтальной оси от установленного 0о до 180о, фиксировать через каждые 10о угол поворота φ и силу фототока I (табл. 2). Таблица 2
3. Проделать необходимые вычисления I/I0 и cos2 φ, занося результаты в табл. 2. 4. Рассчитать степень поляризации Р по формуле (6), взяв максимальное и минимальное значение силы фототока из табл. 1. 5. Построить лепестковую диаграмму с отображением двух графиков на одной диаграмме: экспериментальные данные 6. Построить график I/I0 = f ( cos 2 φ ). Проанализировать график и сделать вывод относительно выполнения закона Малюса.
Задание 3 Изучение эллиптической поляризации 1. Ввести в оптический канал четвертьволновую пластину 2. 2. Измерить силу фототока в зависимости от угла φположения анализатора, через каждые 20о от 0о до 360о (табл. 3) Таблица 3
3. По полученным экспериментальным данным построить лепестковую диаграмму Убедиться в том, что сила тока меняется в пределах от I max до I min, сделать вывод о характере поляризации. 4. Рассчитать отношение полуосей эллипса поляризации:
Задание 4. Исследование круговой поляризации 1. Получить излучение круговой поляризации. Для этого поворачивать пластину «λ/4» на небольшие углы (порядка 10 - 20°) и в каждом положении вращать анализатор, наблюдая изменение интенсивности от I max до I min. То положение, при котором это изменение будет наименьшим, соответствует углу 45° между плоскостью поляризации излучения и оптической осью четвертьволновой пластины. 2. Записать значения фототока в зависимости от угла поворота анализатора в таблицу 4. Таблица 4
3.По полученным экспериментальным данным построить лепестковую диаграмму Убедиться в том, что полученная поляризация действительно соответствует круговой. Таблица 1
Таблица 2
ИСКУССТВЕННАЯ ОПТИЧЕСКАЯ АНИЗОТРОПИЯ
Теоретические сведения На ячейку Керра (композит свинца, лантана, циркония и титана), ориентированную под углом 45° к вертикали, падает монохроматический вертикально поляризованный свет. Электрическое поле, приложенное к материалу ячейки, создает в нем искусственную оптическую анизотропию (двойное лучепреломление). Фазовый сдвиг между обыкновенным и необыкновенным лучом после прохождения световой волной ячейки Керра регистрируется как функция приложенного напряжения. Показано, что фазовый сдвиг пропорционален квадрату напряженности электрического поля создаваемого приложенным напряжением. Коэффициент пропорциональности между фазовым сдвигом и напряженностью поля позволяет определить постоянную Керра. Как правило, эффект Керра демонстрируется с помощью ячейки, заполненной нитробензолом. Поскольку это вещество токсично и требует напряжений порядка нескольких киловольт, то ячейки Керра на основе композита свинца, лантана, циркония и титана представляют собой привлекательную альтернативу. Задачи работы 1. Измерить фазовый сдвиг между обыкновенным и необыкновенным лучом для разных значений величины напряженности электрического поля, приложенного к ячейке. 2. Определить разность потенциалов соответствующую сдвигу обыкновенного и необыкновенного лучей на половину длины волны 3. Построить графическую зависимость 4. Определить постоянную Керра по величине коэффициента углового наклона зависимости
Экспериментальная установка Внешний вид установки для наблюдения эффекта Керра показан на рис.1.
Рис.1 Экспериментальная установка по наблюдению эффекта Керра. Ячейка Керра присоединена напрямую к высоковольтному источнику питания. Напряжение источника может изменяться в пределах от 0 до 1000В. Цифровой вольтметр, присоединенный к источнику, позволяет довольно точно контролировать напряжение. Источником света является He-Ne лазер мощностью 1 мВт. Внимание: лазер долженработать в течение одного часа перед тем, как будут начаты измерения. Это необходимо для стабилизации мощности излучения. Более того, после каждого изменения напряжения приложенного к ячейке Керра, кристаллическая структура перестраивается в течение 5 минут, и только по истечении этого времени можно делать корректные измерения излучаемой интенсивности света. Неполяризованная часть излучения (фоновое излучение) должна быть исключена. Следует учесть, что экспериментальные данные во многом зависят от предыстории состояния ячейки Керра. Для разных ячеек Керра число наблюдаемых максимумов может быть различным. Никогда не смотрите прямо в неослабленный лазерный пучок! Как следует из рисунка 1, вертикально поляризованный свет от гелий-неонового лазера падает на ячейку Керра, которая сориентирована под углом 45° к вертикали. Исходная падающая световая волна может быть представлена в виде суперпозиции двух линейно поляризованных волн, электрические векторы которых синхронно колеблются в направлениях перпендикулярном и параллельном ячейке Керра и вектору напряженности внешнего электрического поля, приложенного к ячейке. Эти две световые волны распространяются сквозь ячейку с разными скоростями. Световая волна, поляризованная параллельно электрическому полю задерживается относительно волны колеблющейся перпендикулярно ему. Это порождает фазовый сдвиг между этими волнами, и свет на выходе из ячейки Керра оказывается, поляризован эллиптически. Это приводит к тому, что анализатор, расположенный за ячейкой Керра и ориентированный перпендикулярно поляризатору перестанет гасить свет, прошедший сквозь ячейку. Когда оптическая разность хода оказывается равной Эта волна повернута на 90° относительно направления поляризации исходной волны, т.е. относительно вертикали. Приложенное в этот момент к ячейке напряжение, тем самым называется “полуволновым напряжением”. В этом случае интенсивность света прошедшего через анализатор, который ориентирован под 90° к поляризатору, покажет максимум. Кремниевый детектор используется для регистрации излучения, вышедшего из анализатора. В 1875 году Керр обнаружил, что стеклянная пластина, к которой приложено сильное электрическое поле, становится двулучепреломляющей. Вскоре стало понятно, что деформация стекла в электрическом поле не является причиной этого эффекта, поскольку он был обнаружен в подобных условиях и в газах и в жидкостях. Композит свинца, лантана, циркония и титана, используемый в данном эксперименте, обладает на два порядка большим двойным лучепреломлением, чем нитробензен, и для того, чтобы изучать электрооптический эффект в этой керамике достаточно напряжения всего в несколько сот вольт. Эта керамика прозрачна для волн c длиной от 0.4 до 5.6 мкм. Ее химический состав описывается формулой Pb 0.9125 La 0.0875 Zr 0.65 Ti 0.3503. Принимая во внимание пропускание света, композит ведет себя как прозрачный поликристалл. Для l = 633 нм его коэффициент пропускания более 60%. Относительно приложенного электрического поля он ведет себя как ферромагнетик, помещенный в магнитное поле. В керамике существуют предварительно поляризованные домены, которые переориентируются под воздействием внешнего электрического поля и элемент становится оптически анизотропным. Элемент может работать как электрооптический модулятор с частотой до 100 кГц. Ширина активного элемента совпадает с расстоянием между электродами. Напряженность электрического поля задается отношением величины приложенного напряжения U к расстоянию между электродами d. Геометрический путь светового луча между электродами равен длине элемента l. Активный элемент (1) укреплен с применением силиконового герметика (2) на изолирующем кольце (3) и вклеен между двух стеклянных пластинок (4). В качестве клея применялся канадский бальзам. Провода (6) закреплены на поверхностях электродов активного элемента и соединены с разъемом типа BNC на рамке (7).
Рис.2 Поперечное сечение композита в ячейке Керра. Активный элемент ячейки Керра 1 представляет собой параллелепипед высотой 8мм, длиной 1.5 мм и шириной 1.4 мм.
Краткая теория Световая волна, электрическое поле которой оссцилирует параллельно внешнему электрическому полю называется “необыкновенной” волной. Волна, электрическое поле которой оссциллирует перпендикулярно внешнему электрическому полю называется обыкновенной. Если показатели преломления необыкновенной и обыкновенной волн обозначить, как
что соответствует разности фаз:
где l - длина волны света в вакууме (l = 633 нм). Можно показать, что фазовый сдвиг пропорционален длине l и квадрату поляризации P. Если предположить, что поляризация P является линейной функцией напряженности электрического поля и коэффициент пропорциональности обозначить
гд е K - постоянная Керра. Напряженность поля E, приложенное напряжение U и расстояние между электродами d связаны соотношением:
Интенсивность света, прошедшего анализатор может быть вычислена для данной конфигурации оборудования (поляризатор и анализатор, скрещенные под 45° с электрическим полем в активном элементе ячейки Керра) из соотношения:
где I0 – интенсивность света, вышедшего из анализатора в том случае, когда плоскости пропускания анализатора и поляризатора совпадают, а электрическое поле, приложенное к ячейке Керра равно нулю. После подстановки (2) в (4) с учетом (3) получаем:
Из этого уравнения следует:
где Зависимость U2 от значений
Порядок выполнения работы
Все измерения следует проводить только в темном помещении! Лазер необходимо включать за 1 час до начала эксперимента, чтобы стабилизировать его излучение! 1. Изменяя напряжение на ячейке Керра от 300 В до 1000 В с шагом 50 В, проведите измерения интенсивности света, падающего на анализатор. Нельзя во время эксперимента превышать напряжение 1000 В, иначе произойдет разрушение PLZТ! После каждого изменения величины подаваемого напряжения на ячейку Керра необходимо выдерживать около 5 минут и затем проводить измерения! 2. Результаты измерений занести в таблицу: (следует добавить столбцы в табл.)
3. Сделайте расчет величин:
4. Постройте графическую зависимость 5. Представьте результаты графически 6. Оцените точность, полученных результатов.
1. Пример измерения относительной интенсивности люминесценции как функции напряжения приложенного к ячейке.
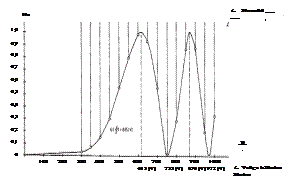
В таблице 1 представлены экспериментальные результаты пробного эксперимента. Соответствующий график приведен на рис.3.
Рис.3 Относительная интенсивность излучения, как функция напряжения приложенного к ячейке и соответствующего ему фазового сдвига. Специально рассчитан и нанесен на график фазовый сдвиг, соответствующий максимумам и минимумам интенсивности излучения. При напряжении в 615 В интенсивность излучения достигает максимума в первый раз. В этом случае обыкновенный и необыкновенный лучи сдвинуты по фазе на величину, равную
Таблица 1
2. Определение постоянной Керра.
На рис.4 представлен квадрат приложенного напряжения как функция фазового сдвига между обыкновеннным и необыкновенным лучами. Линейная аппроксимация данных дает для коэффициента углового наклона прямой значение 1.36×103 (В2/градус). Для длины активного элемента l = 1.5 мм и его толщины d = 1.4 мм получаем значение постоянной Керра
Рис.4 Квадрат напряжения приложенного к ячейке как функция фазового сдвига между обыкновенным и необыкновенным лучом.
Примечание Величина постоянной Керра может быть различной в зависимости от типа материала активного элемента.
Электрооптический модулятор
Активный элемент ячейки Керра может быть использован как электрооптический модулятор, если к нему приложить одновременно постоянное и переменное напряжения. Для проверки работы модулятора необходимо собрать схему (рис.5) и провести следующий эксперимент. Выход генератора сигналов переменного тока соединим последовательно с источником постоянного напряжения величиной 500В. Частоту переменного сигнала подбираем так, чтобы она попала в акустический диапазон. Суммарный сигнал подаём на ячейку Керра. Вместо вольтметра на выходе приемного усилителя подключаем звуковую акустическую систему. Сигнал с выхода приемного усилителя подаём на вход динамика. Регулируя амплитуду переменного напряжения на генераторе, добиваемся качественного звучания динамика. Изменяя частоту генератора переменного сигнала вблизи её значения порядка 1кГц, наглядно демонстрируем работу электрооптического модулятора.
Рис.5 Электрооптический модулятор.
ПРИЛОЖЕНИЕ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ «ГОРНЫЙ»
Кафедра общей и технической физики
Общая физика ВОЛНОВАЯ ОПТИКА
Поляризация световых волн. Искусственная оптическая анизотропия
Лабораторный практикум
САНКТ-ПЕТЕРБУРГ УДК 535.41/42 + 535.5 (075.80) ББК 22.34
Общая физика. ВОЛНОВАЯ ОПТИКА. Поляризация световых волн. Искусственная оптическая анизотропия: Лабораторный практикум / А.С.Мустафаев, С.В. Егоров. Национальный минерально-сырьевой университет «Горный». СПб, 2012. 38 с. ISBN 5-94211-162-6
В лабораторном практикуме представлены работы по всем основным оптическим явлениям: дисперсии, поляризации, поглощению света, искусственной оптической анизотропии, вызываемой электромагнитными полями, и вращению плоскости поляризации. Практикум предоставляет возможность студентам познакомиться с явлениями, лежащими в основе современных оптических т
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.76 (0.016 с.) |

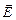 и магнитного поля
и магнитного поля 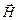 взаимно перпендикулярны и одновременно перпендикулярны направлению распространения волны
взаимно перпендикулярны и одновременно перпендикулярны направлению распространения волны 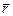 (рис.1). Плоскость, проведенную через направления
(рис.1). Плоскость, проведенную через направления 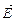 и
и 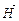 и ориентацию в пространстве плоскости колебаний электрического вектора. Если для некоторого пучка света плоскость колебаний электрического вектора не изменяет положение в пространстве, то такой свет называют линейно-поляризованным.
и ориентацию в пространстве плоскости колебаний электрического вектора. Если для некоторого пучка света плоскость колебаний электрического вектора не изменяет положение в пространстве, то такой свет называют линейно-поляризованным.
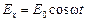 и
и 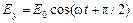 , где w – частота световой волны, то в каждый момент времени t эти составляющие складываются. Результирующий вектор, оставаясь постоянным по величине, вращается с частотой w, а его конец описывает окружность. В этом случае говорят, что свет имеет круговую поляризацию.
, где w – частота световой волны, то в каждый момент времени t эти составляющие складываются. Результирующий вектор, оставаясь постоянным по величине, вращается с частотой w, а его конец описывает окружность. В этом случае говорят, что свет имеет круговую поляризацию.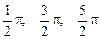 и т.д., то конец электрического вектора будет описывать эллипс и в этом случае говорят об эллиптической поляризации светового пучка. Таким образом, имеется пять типов поляризованного света:
и т.д., то конец электрического вектора будет описывать эллипс и в этом случае говорят об эллиптической поляризации светового пучка. Таким образом, имеется пять типов поляризованного света: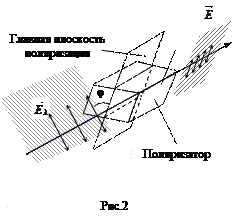
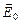 на две составляющие, лежащие в главной плоскости поляризатора: Е || = Е 0cosj, и перпендикулярную составляющую E ^ = E 0sinj, где j – угол между плоскостью колебаний электрического вектора, падающего на поляризатор излучения, и главной плоскостью поляризатора. Поскольку поляризатор пропускает излучение только с составляющей вектора
на две составляющие, лежащие в главной плоскости поляризатора: Е || = Е 0cosj, и перпендикулярную составляющую E ^ = E 0sinj, где j – угол между плоскостью колебаний электрического вектора, падающего на поляризатор излучения, и главной плоскостью поляризатора. Поскольку поляризатор пропускает излучение только с составляющей вектора 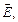 лежащей в главной плоскости, то выходящее излучение имеет интенсивность
лежащей в главной плоскости, то выходящее излучение имеет интенсивность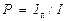 . (2)
. (2)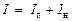 , где I н – интенсивность неполяризованного компонента. Поскольку 0 < I н< I, то степень поляризации может меняться в пределах 0 < Р < 1.
, где I н – интенсивность неполяризованного компонента. Поскольку 0 < I н< I, то степень поляризации может меняться в пределах 0 < Р < 1.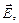 то интенсивность прошедшего излучения будет меняться от максимального значения I max до минимального I min. В первом положении поляризованный компонент проходит полностью, а неполяризованный уменьшается по интенсивности вдвое:
то интенсивность прошедшего излучения будет меняться от максимального значения I max до минимального I min. В первом положении поляризованный компонент проходит полностью, а неполяризованный уменьшается по интенсивности вдвое:
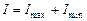 . Подставляя последние соотношения в (2) получим формулу для расчета степени поляризации при обработке экспериментальных данных:
. Подставляя последние соотношения в (2) получим формулу для расчета степени поляризации при обработке экспериментальных данных: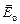 ), так и в необыкновенной (
), так и в необыкновенной (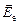 ) совершаются согласованно (когерентно). И в дальнейшем будем индексом о - обозначать обыкновенную волну; индексом е – необыкновенную.
) совершаются согласованно (когерентно). И в дальнейшем будем индексом о - обозначать обыкновенную волну; индексом е – необыкновенную.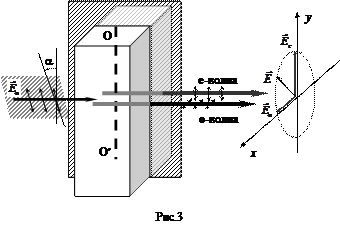
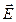 движется по эллипсу (рис.3):
движется по эллипсу (рис.3):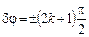 , k = 0, 1, 2, … Уравнение эллипса преобразуется при этом к виду
, k = 0, 1, 2, … Уравнение эллипса преобразуется при этом к виду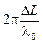 . Используя (6), получим
. Используя (6), получим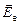 в первом случаеи
в первом случаеи 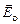 во втором).
во втором).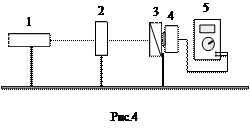
 .
.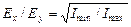 .
.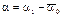
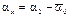
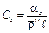
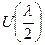 .
. - квадрат приложенного напряжения как функцию фазового сдвига между обыкновенным и необыкновенным лучами. Показать линейный характер этой зависимости.
- квадрат приложенного напряжения как функцию фазового сдвига между обыкновенным и необыкновенным лучами. Показать линейный характер этой зависимости.
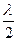 , суперпозиция волн на выходе из ячейки дает линейно поляризованную волну.
, суперпозиция волн на выходе из ячейки дает линейно поляризованную волну.
 и
и  , а длину пути проходимого светом в активном элементе как l, то оптическая разность хода необыкновенной и обыкновенной волн запишется как
, а длину пути проходимого светом в активном элементе как l, то оптическая разность хода необыкновенной и обыкновенной волн запишется как ,
, , (1)
, (1) , то можно получить следующее соотношение:
, то можно получить следующее соотношение: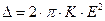 , (2)
, (2) . (3)
. (3) , (4)
, (4) . (5)
. (5)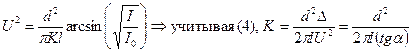 (6)
(6) , а градусы необходимо выразить в радианах.
, а градусы необходимо выразить в радианах.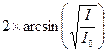 дает примерно прямую линию. Из этой зависимости и определяется значение постоянной Керра K.
дает примерно прямую линию. Из этой зависимости и определяется значение постоянной Керра K.
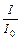 и
и 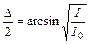 , где
, где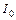 - максимальное значение интенсивности света, падающего на анализатор. Заполните соответствующие графы таблицы.
- максимальное значение интенсивности света, падающего на анализатор. Заполните соответствующие графы таблицы.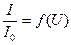 . Соедините точки плавной кривой. Определите по графику «напряжение соответствующее
. Соедините точки плавной кривой. Определите по графику «напряжение соответствующее  »: при этом напряжении внешнего электрического поля разность фаз обыкновенного и необыкновенного лучей, прошедших данный образец, становится равной 900. Следовательно, этому напряжению соответствует первый максимум на графике.
»: при этом напряжении внешнего электрического поля разность фаз обыкновенного и необыкновенного лучей, прошедших данный образец, становится равной 900. Следовательно, этому напряжению соответствует первый максимум на графике. . Выполните линейную аппроксимацию экспериментальных данных. Определите по графику постоянную Керра (см. формулу (6)).
. Выполните линейную аппроксимацию экспериментальных данных. Определите по графику постоянную Керра (см. формулу (6)).










 .
.




