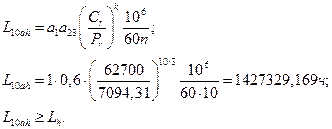Проверка червячного колеса на прочность и жесткость

Размеры, мм	Грузоподъемность, кH
		Т		С	е
					0,4	62,7

Радиальные реакции опор от сил в зацеплении:

Горизонтальная плоскость:

Проверка:

Вертикальная плоскость:

Проверка:

 

Произвольная плоскость:

Проверка:

Суммарные реакции опор:

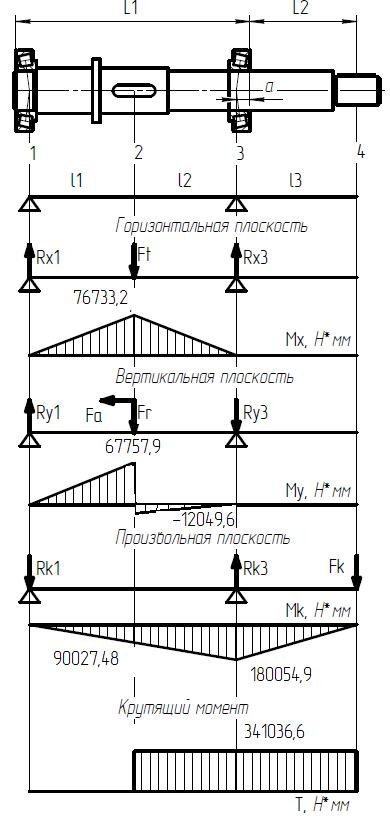
Определение внутренних силовых факторов

Определяем внутренние силовые факторы для опасных сечений:

Реакции от внутренних силовых факторов определены ранее.

Эпюры внутренних силовых факторов приведены на рис.7, при этом

крутящий момент численно равен вращающемуся:

 

Mk = T2 = 341,03 кН*м;

 

Из рассмотрения эпюр внутренних силовых факторов и конструкции узла следует, что опасными являются сечения:

 

2-2 - Концентрация напряжения в рассматриваемом сечении

вызывается наличием червячного колеса установленного с натягом.

Сечение нагружено изгибающим и крутящим моментами.

Концентратор напряжений - посадка с натягом.

 

3-3 - Концентрация напряжения в рассматриваемом сечении

вызывается наличием подшипника. Сечение нагружено изгибающим и

крутящим моментами. Концентратор напряжений - посадка с натягом.

 

4-4 - Концентрация напряжения в рассматриваемом сечении

вызывается наличием шпоночного паза по ГОСТ 23360-78

(исполнение 1). Сечение нагружено крутящим моментом. Данное сечение рассматривается как сечение со шпоночным пазом, выполненным концевой фрезой.

Определим силовые факторы для опасных сечений.

 

Сечение 2-2

 

Изгибающие моменты:

- горизонтальная плоскость

 

 

- вертикальная плоскость слева от сечения

 

 

- вертикальная плоскость справа от сечения

 

 

- момент от консольной силы

 

 

Суммарный изгибающий момент

 

 

Сечение 3-3

 

Изгибающий момент от консольной силы:

 

 

Сечение 4-4

Крутящий момент:

 

Расчёт подшипника на заданный ресурс

Схема установи подшипников - врастяжку.

Для принятых подшипников из таблицы находим: Сr=62700 H;е=0,4;

Найдем необходимые для нормальной работы радиально-упорных подшипников осевые силы:

Находим эквивалентную силу:

,

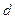
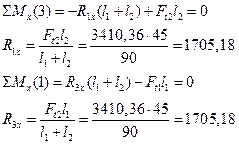
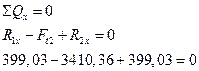
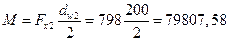
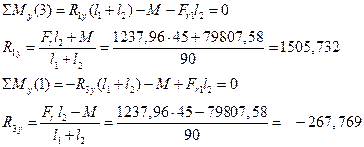
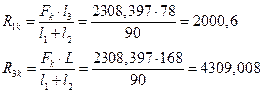
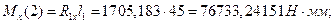
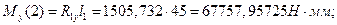
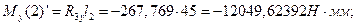
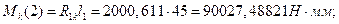
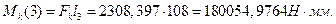
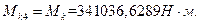
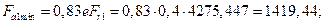
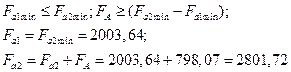
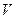где - коэффициент, учитывающий какое кольцо подшипника вращается, так как в нашем случае вращается внутреннее кольцо, то ;

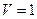– коэффициент радиальной нагрузки, ;

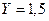– коэффициент осевой нагрузки;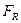

– максимальная радиальная нагрузка на подшипники, в нашем случае

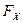– максимальная осевая нагрузка на подшипник, ;

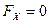- температурный коэффициент, при ;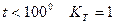

– коэффициент, учитывающий динамические нагрузки, .

 

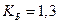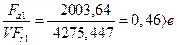Отношение , тогда для опоры 1: Х=0,44, У=1.

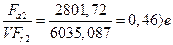Отношение , тогда для опоры 2: Х=0,44, У=1.

Теперь найдем расчётный ресурс:

 

В нашем случае условие выполняется, следовательно, подшипник проработает требуемый ресурс.