
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Текстильной и легкой промышленности»Содержание книги
Поиск на нашем сайте
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РФ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ ЗАОЧНЫЙ ИНСТИТУТ ТЕКСТИЛЬНОЙ И ЛЕГКОЙ ПРОМЫШЛЕННОСТИ» Кафедра информатики Алгоритмизация и программирование Сборник задач и упражнений (Microsoft Office 2003, Excel и VBA) Для студентов всех специальностей Москва 2010 Составители: В.В. Серов, проф. д.т.н., И.М. Шаронова, доц. к.т.н.
Алгоритмизация и программирование. Сборник задач и упражнений По информатике (Microsoft Office 2003, Excel и VBA) /Российск. заочн. ин-т текстил. и легк. пр-сти; Сост. В.В.Серов, И.М.Шаронова М., 2009, __с.
Предназначено для студентов всех специальностей.
Введение В процессе изучения курса «Информатика»студенты должныознакомиться с современными техническими и программными средствами, предназначенными для решения инженерных и экономических задач. Выполняя лабораторные работы, студенты осваивают методы решения задач: разработки алгоритма, написания текста программы, ее отладки, оформления отчета о проделанной работе. В первой части пособия приведены задания, которые выполняются на лабораторных работах. Преподаватель указывает студентам какие именно задания должны быть выполнены и какое прикладное программное обеспечение следует использовать для решения поставленной задачи (Excel или VBA).
Методические указания
Рис.8.Пример таблицы Для объединения нескольких ячеек в одну следует выделить их, выбрать команды Формат → Ячейки, вкладку Выравнивание и отметив флажокв строке Объединение ячеек, щелкнуть кнопку ОК. Если отметить флажок в строке Переносить по словам, текст в ячейке будет записан в нескольких строчках.
Желательно выравнивать этот текст по центру по горизонтали и по вертикали, выбрав соответствующие строки в раскрывающихся списках этой вкладки – Выравнивание (по горизонтали, по вертикали). Здесь же в окне Ориентация можно изменить направление текста. Пример отформатированной таблицы приведен на рисунке 8.
Рис.9.Форматирование и выравнивание Примеры решения задач Определение объема рулона ткани Пример 1. Требуется определить объемы нескольких рулонов ткани, сложенных в штаб (рис.10), а также их общий объем. Объем рулона вычисляется по формуле:
Рис. 10. Рулон ткани, сложенный в штаб
Аргументы Эта строка служит пояснением (комментарием). Если позднее надо будет повторить вычисления для других исходных данных, такие пояснения облегчат работу. В строках 2, 3 и 4 записаны значения ширины, длины и высоты каждого из трех рулонов. Для первого рулона эти величины размещены в ячейках A2, B2 и С2. В ячейке D2 записана формула: =A2*B2*C2. После нажатия клавиши Enter в ячейке получится число – объем рулона. Снова выделим ячейку D2. В строке формул увидим формулу, по которой выполнялись вычисления. Скопируем эту формулу в ячейки D3 и D4. Для этого щелкнем по черному квадратику в правом нижнем углу выделенной ячейки D2 и, не отпуская клавишу мышки протянем ее до ячейки D4. В ячейках D3 и D4 увидим объемы второго и третьего рулонов.
Рис. 11. Расчет объема рулона ткани Для того, чтобы определить общий объем всех рулонов ткани (D2-D4), следует выделить ячейки, в которых записаны объемы отдельных рулонов и щелкнуть на кнопке «Автосуммирование» Рис. 13 Вычисление площади фигуры методом трапеций
Создадим таблицу, в первой строке которой комментарии – имена переменных, а в первом столбце – номера точек (рис. 15). В Excel площадь фигуры может быть вычислена следующим образом. В столбцы В и С рабочего листа введем координаты точек ломаной, ограничивающей фигуру. При этом будем записывать координаты, обходя фигуру по часовой стрелке. Для того чтобы ломаная была бы замкнута, координату начальной точки повторим дважды: в начале и в конце таблицы (рис. 15).
Вычисление площади фигуры начнем с вычисления площади первой трапеции. Её основания равны значениям =0,5*(C3+C2)*(B3-B2) (*)
Рис. 15 Щелкнув левой кнопкой мыши или нажав клавишу Enter, получим площадь первой трапеции. Выделим ячейку D3, поставим курсор мыши на маркер заполнения и протянем мышь вниз, не отпуская её кнопки, до ячейки D7. В ячейки D4÷D7 будет скопирована формула (*), выполнены вычисления. В этих ячейках появятся величины площадей остальных трапеций. Площадь всей фигуры получим после суммирования площадей всех трапеций с помощью кнопки «Автосуммирование» стандартной панели инструментов. Обратите внимание на то, что в ячейках D6 и D7 значения Функции Excel В Excel имеются функции, которые для заданных значений =СРЗНАЧ(А1:А10) Не следует набирать эту формулу с помощью клавиатуры. Надо использовать следующую последовательность действий: 1. Разместить в ячейке А12 символ «=». 2. Нажать кнопку «Вставка функций» 3. В открывшемся окне выбрать функцию СРЗНАЧ и нажать кнопку ОК в правом нижнем углу окна. Появится окно «Аргументы функции». 4. Щелкнуть на кнопке в конце строки «число 1» в окне «Аргументы функции»., выделить диапазон А1-А10, нажать в этом окне кнопку ОК. В ячейке А12 появится результат.
Рис. 16 Окно «Мастер функций»
Точно также вычисляются функции МАКС, МИН, СТАНДОТКЛОН. Первая из них предназначена для вычисления максимального значения в наборе чисел, вторая - минимального, а третья – для определения величины среднеквадратического отклонения. Для вызова этих функций можно использовать категорию «Полный арифметический перечень».
Финансовые функции Excel 1. Функция ПЛТ вычисляет величину периодического платежа по ссуде при условии постоянства платежей и процентной ставки.
Для вычисления величины платежа следует используя Мастер функций записать в ячейке рабочего листа вызов этой функции: =ПЛТ (ставка; кпер; пс;бс;тип) Ставка — процентная ставка по ссуде за период. Например, если получена ссуда на автомобиль под 10 процентов годовых и делаются ежемесячные выплаты, то процентная ставка за месяц составит 10%/12 или 0,83%. В качестве значения аргумента ставка нужно ввести в формулу 10%/12 или 0,83% или 0,0083. Кпер — общее число периодов выплат по ссуде. Например, если получена ссуда на 4 года под автомобиль и делаются ежемесячные платежи, то ссуда имеет 4*12 (или 48) периодов. В качестве значения аргумента кпер в формулу нужно ввести число 48. Пс — сумма, которую банк выдает под проценты. Бс — требуемое значение будущей стоимости, или остатка средств после последней выплаты. Если аргумент «Бс» опущен, то он полагается равным 0 (нулю), т. е. для займа, например, значение «Бс» равно 0. Тип — число 0 (нуль) или 1, обозначающее, когда должна производиться выплата.
Примечания 1. Если равны нулю параметры «Бс» и «Тип», то их можно опустить, а в списке параметров, в скобках после имени функции, указать только три первых параметра: «Ставка», «Кпер» и «Пс». 2. Выплаты, возвращаемые функцией ПЛТ, включают основные платежи и платежи по процентам, но не включают налогов, резервных платежей или комиссий, которые иногда связываются со ссудой. 3. При задании аргументов «ставка» и «кпер» следует обратить внимание на единицы измерения. Если делаются ежемесячные выплаты, например, по четырехгодичному займу из расчета 10 процентов годовых, то для задания аргументов «ставка» (процентная ставка на 1 месяц) и «кпер»(количество месяцев) используются величины 10%/12 и 4*12 соответственно. Если делаются ежегодные платежи по тому же займу, то надо задать аргумент «ставка» равным 10 %, а аргумент «кпер» - равным 4. 4. Для нахождения общей суммы, выплачиваемой на протяжении всего времени выплат, умножьте возвращаемое функцией ПЛТ значение на «кпер». Обратите внимание на то, что в финансовых функциях получаемые деньги представляются положительными числами, а выплачиваемые – отрицательными. Пример 1. Определитьразмеры ежемесячной и ежегодной выплат по 25-летней ипотечной ссуде, если цена покупки равна 5200000руб., первый взнос составляет 20% (ссуда берется на остальные 80%), процентная ставка равна 8%. Размер ссуды в таблице представлен отрицательным числом, так как банк эти деньги выплачивает клиенту. Фрагмент рабочего листа с решением задачи приведен на рисунке 17.
Рис. 17 2. Функция ПС может быть использована для вычисления суммы, которую надо положить в банк для того, чтобы в течение определенного времени получать периодические выплаты. Для вычисления Этой суммы следует записать в ячейке рабочего листа вызов функции: =ПС (ставка; кпер; пс; бс; тип) Параметры «ставка», «кпер», «бс» и «тип» те же, что и в функции ПЛТ, а «пс» — выплата, производимая в каждый период и не меняющаяся за все время выплат.
Пример 2. Какую сумму надо положить в банк сегодня для того, чтобы в течение 20 лет получать 500руб ежемесячно, если процентная ставка равна 8% годовых? Параметры: ставка – 8% годовых., 8%/12 –ставка за месяц; кпер – количество месяцев, в течение которых будут производиться выплаты. Кпер=20*12; пс – деньги, выплачиваемые в конце каждого месяца. В этом примере пс=500руб. Остальные параметры не используем. Фрагмент рабочего листа с решением задачи приведен на рисунке 18.
Рис. 18 Задания Вычисление функции
Вычислить значение функции: 1.1 1.2. 1.3. Примечание. Если для определения значения функции
1.4. Примечание. При вычислении функции
2.4 Задания 2.5 – 2.8. Разработать блок-схему и программу вычисления функции 2.5 2.6 2.7 2.8
Рис.22 Анализ качества продукции
6.1. Определить максимальное, минимально и среднее значения среди измеренных величин, а также среднеквадратическое отклонение (см. Функции Excel на стр. 14). .
Рис. 23 Выкроена партия деталей изделий, например воротничков рубашки. Из этой партии отобраны 10 деталей. На практике выборки больше. В этой выборке измерена ширина воротника в концах. Результаты измерений представлены в таблице на рис. 23. Требуется определить максимальное, минимальное и среднее значения среди измеренных величин, а также среднеквадратическое отклонение. Эти величины используются для решения вопроса о качестве выполнения технологической операции раскроя изделия. Результаты расчета представить на рабочем листе Excel (рис. 23).
При выполнении задания измените (уменьшите или увеличьте) некоторые из приведенных в диапазоне В2-В11 значений на величину ±0,25. 7. Задачи на вычисление процентов
7.1.. Продавец продал партию изделий за 12 000 рублей. Прибыль от продажи составила 2,5%. Какую сумму прибыли получил продавец?
7.2. Предприниматель собирает деньги на покупку нового оборудования и положил в банк 100 000 рублей. Через 2 года 6 месяцев на счете было 120 000 рублей. Сколько процентов (простых) выплачивает этот банк в год?
Примечание. В банк положили сумму P. Если в конце каждого периода времени (год, квартал или месяц) эта сумма увеличивается на r процентов, то говорят, что начисляются простые проценты. Здесь
Простые проценты начисляются на одну и ту же исходную сумму, которая не изменяется от периода к периоду, не включает начисленные проценты.
7.3. Банк начисляет ежегодно 8% сложных. Клиент положил в этот банк 20000 руб. Какая сумма будет на его счете через 5 лет? Какая сумма была бы на его счете, если бы банк начислял простые проценты? Примечание. Сложные проценты начисляются на наращенную сумму, т.е. сумму, которая имеется на счете в конце предыдущего периода, включая начисленные проценты. Сумма S, полученная через t периодов в результате начисления сложных процентов вычисляется по формуле:
Здесь
Финансовые функции Excel 8.1. Рассчитать ежемесячные (и ежегодные) выплаты по ссуде с помощью функции ПЛТ (см. пример стр. 17).
Размер ссуды – 500000 Первоначальный взнос - 35% Годовая процентная ставка 10% Срок погашения ссуды – 15 лет.
8.2. Вас просят дать в долг 10000руб. и обещают возвращать по 2000руб. в течение 6 лет. Будет ли выгодна эта сделка при годовой ставке 5%. Использовать функцию ПС (см. пример стр. 15-17).
8.3. Студент будет учиться в другой стране. Ежегодная плата за обучение составляет 1500$, банковский процент - 4%. Сколько денег надо сейчас положить в банк для того, чтобы в течение 5 лет каждый год выплачивать сумму 1500$. Использовать функцию ПС. Описание подпрограммы и пример использования функции смотрите на страницах 15-17.
Литература
1. Гарнаев А. Ю. Использование Excel и VBA в экономике и финансах.- СПб.: БХВ – Санкт-Петербург, 1999 2. Ларсен Р. У. Инженерные расчеты в Excel – М.: Издательский дом «Вильямс», 2002 3. Комиссаров О. Ю., Скирута М. А. Одежда и компьютер. – М.: Легпромбытиздат, 1991 4. Серов В. В., Шаронова И. М., Яснова Л. Н. Лабораторный практикум по информатике, часть 2 – М.: РосЗИТЛП, 2006 5. Серов В. В., Шаронова И. М., Яснова Л. Н. ИНФОРМАТИКА. Методические указания и контрольные задания. - М.: РосЗИТЛП, 2008
Содержаниe стр.
Введение…………………………………………………………..3 Методические указания………………………………………….3 1. Программирование на рабочем листе……………………3 2. Примеры решения задач…………………………………..9 2.1. Определение объема рулона ткани…………………9 2.2. Определение расхода ниток на пошив изделия ….10 2.3.Определение площади лекала детали изделия …….11 2.4. Вычисление определенного интеграла…………….12 2.5. Функции Excel……………………………………...14 2.6.Финансовые функции Excel…………………………15 Задания
1. Вычисление функции……………………………………...18 2. Циклы. Построение графиков функций………………….19 3. Определение объема и массы рулона ткани …………….19 4. Расчет расхода ниток на строчку…………………………21 5. Определение площади лекала детали изделия…..………21 6. Анализ качества продукции ………………………………23 7. Задачи на вычисление процентов………………………...24 8. Финансовые функции Excel……………………………….24 Литература…………………………………………………….......25
Редактор О.Л.Лобанова План 2009г., поз..
Сдано в производство. Формат 60х84/16. Бумага офсетная. Печать офсетная. Усл. печ. л._____. Уч.-изд. л. ____ Тираж 1000 экз. Заказ. Цена договорная.
Российский заочный институт текстильной и легкой промышленности. 123423 Москва ул. Демьяна Бедного, 7.
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РФ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ ЗАОЧНЫЙ ИНСТИТУТ ТЕКСТИЛЬНОЙ И ЛЕГКОЙ ПРОМЫШЛЕННОСТИ» Кафедра информатики
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.238.13 (0.014 с.) |



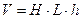
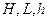 (рис.10) задаются в метрах. На рисунке 11 приведен фрагмент рабочего листа с решением поставленной задачи. Первая строка таблицы в расчетах не используется. В ней записаны только имена аргументов.
(рис.10) задаются в метрах. На рисунке 11 приведен фрагмент рабочего листа с решением поставленной задачи. Первая строка таблицы в расчетах не используется. В ней записаны только имена аргументов.
 стандартной панели инструментов. В некоторых версиях Excel следует выделять, по крайней мере, еще одну пустую ячейку после последней ячейки с данными. В этой ячейке и будет помещен результат суммирования.
стандартной панели инструментов. В некоторых версиях Excel следует выделять, по крайней мере, еще одну пустую ячейку после последней ячейки с данными. В этой ячейке и будет помещен результат суммирования. Рис. 14.
Рис. 14.
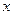 и ломаной линией, проходящей через точки А,1, 2, 3, 4,В, а другая - той же осью
и ломаной линией, проходящей через точки А,1, 2, 3, 4,В, а другая - той же осью 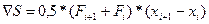
 и
и  , записанным в ячейках С2 и С3. Высота трапеции представляет собой разность
, записанным в ячейках С2 и С3. Высота трапеции представляет собой разность  . Значение
. Значение  записано в ячейке В3, а
записано в ячейке В3, а  - в ячейке В2. Поскольку количество трапеций на единицу меньше количества точек, через которые проходит ограничивающая фигуру ломаная, для дальнейших вычислений ячейку D2 удобнее оставить пустой. Формулу, по которой вычисляется
- в ячейке В2. Поскольку количество трапеций на единицу меньше количества точек, через которые проходит ограничивающая фигуру ломаная, для дальнейших вычислений ячейку D2 удобнее оставить пустой. Формулу, по которой вычисляется  площадь первой трапеции, запишем в ячейке D3:
площадь первой трапеции, запишем в ячейке D3:
 меньше нуля. Это не ошибка. Записывая координаты точек 1─5 (рис. 14), мы обходили фигуру по часовой стрелке. Поэтому высоты четвертой и пятой трапеций, вычисленные по формулам
меньше нуля. Это не ошибка. Записывая координаты точек 1─5 (рис. 14), мы обходили фигуру по часовой стрелке. Поэтому высоты четвертой и пятой трапеций, вычисленные по формулам  и
и  отрицательны.
отрицательны. вычисляют суммы элементов массива, находят среднее и среднеквадратическое значения, стандартное отклонение. Всего в Excel более трехсот функций. Функция обеспечивает выполнение определенной последовательности операций над исходными данными – аргументами. Пусть, например, требуется вычислить среднее значение некоторого набора данных, записанных в ячейках А1:А10. Для вызова функции следует в ячейку рабочего листа, допустим в А12, поместить символ «=», за ним – имя функции, а далее в круглых скобках – записать аргумент - диапазон А1-А10:
вычисляют суммы элементов массива, находят среднее и среднеквадратическое значения, стандартное отклонение. Всего в Excel более трехсот функций. Функция обеспечивает выполнение определенной последовательности операций над исходными данными – аргументами. Пусть, например, требуется вычислить среднее значение некоторого набора данных, записанных в ячейках А1:А10. Для вызова функции следует в ячейку рабочего листа, допустим в А12, поместить символ «=», за ним – имя функции, а далее в круглых скобках – записать аргумент - диапазон А1-А10: и выбрать категорию функций «Статистические». Откроется приведенное на рисунке 16 окно «Мастер функций – шаг 1 из 2».
и выбрать категорию функций «Статистические». Откроется приведенное на рисунке 16 окно «Мастер функций – шаг 1 из 2».



 этого примера применяется Excel, то при вычислении числа π и стандартных функций, таких как Sin(x), Cos(x), Exp(x) и т. д., следует использовать Мастер функций.
этого примера применяется Excel, то при вычислении числа π и стандартных функций, таких как Sin(x), Cos(x), Exp(x) и т. д., следует использовать Мастер функций.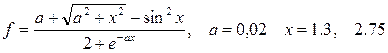
 . Полученное значение функции вывести на экран дисплея или в ячейку рабочего листа.
. Полученное значение функции вывести на экран дисплея или в ячейку рабочего листа.

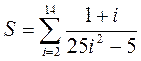
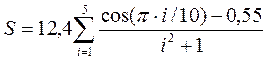

 - количество периодов времени, не обязательно целое число. Полученная в результате начисления простых процентов сумма S вычисляется по формуле:
- количество периодов времени, не обязательно целое число. Полученная в результате начисления простых процентов сумма S вычисляется по формуле:




