Пояснения к выполнению эпюра 1

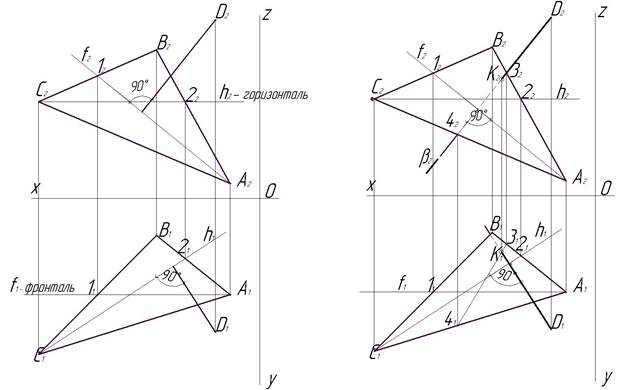
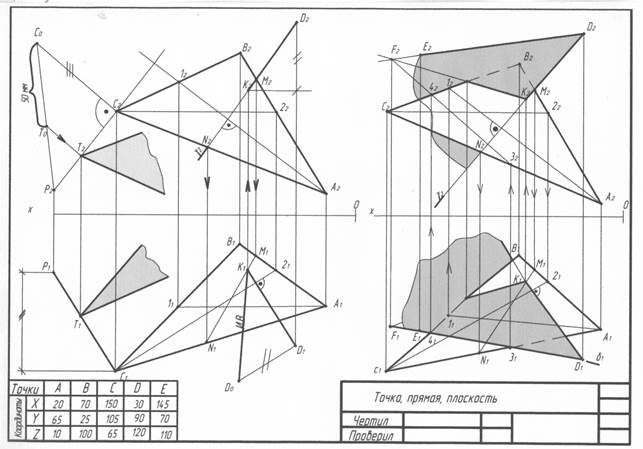
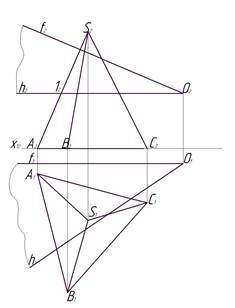
Задача 1

В первой задаче контрольной работы требуется найти рас­стояние от точки D до плоскости треугольника ABC. Кратчайшее расстояние от точки до плоскости есть перпендикуляр, опущен­ный из данной точки на эту плоскость.

Этап 1 ( рис. 1). Для решения этой задачи необходимо, прежде всего, провести горизонталь (h2) из какой-нибудь вершины треугольника ABC на фронтальной плоскости проекций (П 2) и фронталь (f1) – на горизонтальной плоскости проекций (П 1) из любой вершины ΔАВС, удобной для этого построения. Обозначив точку пересечения фронтали со стороной ΔАВС на горизонтальной плоскости проекций точкой 11, нужно найти ее проекцию (по проекционной связи) на фронтальной проекции ΔАСВ, это будет точка 12.

 

Рис. 1 Этап 1 Рис. 2 Этап 2

Таким же образом находятся точки 22 и 21, используя горизонталь (h2). Из точки D2 опускаем ⊥ (перпендикуляр) на f2 (отрезок А212) и из точки D1 опускаем ⊥ на h1 (отрезок С1 21).

 

Этап 2 ( рис. 2). Необходимо найти основание перпендикуляра как точку пересечения прямой DK и плоскости, заданной ΔАВС. Для этого продолжаем перпендикуляр из точки D2 (на фронтальной плоскости проекций) до пересечения со стороной А2С2 – обозначаем точку 42. Пересечение перпендикуляра со стороной А2В2 дает нам точку 32. Заключаем прямую 4232 во вспомогательную проецирующую плоскость β2, это действие дает нам возможность найти проекцию отрезка 4232 на горизонтальной плоскости проекций (П 1) в плоскости ΔАВС – это отрезок 4131. Находим точку пересечения отрезка 4131 с перпендикуляром, опущенным из точки D1 и обозначаем ее К1. Используя проекционную связь, находим точку К2 на перпендикуляре, который опущен из точки D2. Таким образом, мы нашли точку пересечения перпендикуляра, опущенного из точки D на плоскость, заданную ΔАВС, на обеих проекциях.

 

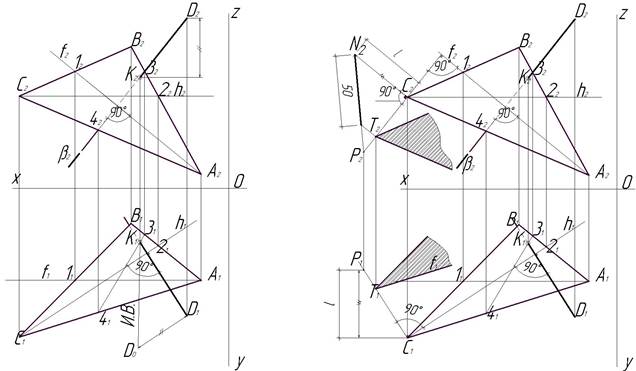
Этап 3 (рис. 3). Следующий этап выполнения задания содержит в себе нахождение натуральной величины перпендикуляра DК.

Это действие можно проводить на любой из плоскостей проекций, мы выбираем горизонтальную плоскость и начинаем построение с восстановления перпендикуляра к отрезку D1К1 в точке D1 (пока произвольной длины). Переходим на фронтальную плоскость проекций и находим расстояние от точки К2 до D2 как разность их высот по отношению к оси Х. Найденное расстояние откладываем на восстановленном перпендикуляре к отрезку D1К1 в точке D1 на горизонтальной плоскости проекций. Отмечаем точку D0. Точку D0 соединяем с точкой К1. Отрезок D0К1 – является натуральной (истинной) величиной перпендикуляра DК к плоскости, заданной ΔАВС. Этот способ нахождения истинной величины расстояния от точки, лежащей вне плоскости, до плоскости называется способом прямоугольного треугольника.

 

 

Рис. 3 Этап 3 Рис. 4 Этап 4

 

Задача 2

Этап 4 (рис. 4). На этом этапе необходимо решить вторую задачу эпюра 1, т.е. построить плоскость, параллельную плоскости, заданной треугольником АВС, и отстоящую от неё на 50 мм. Построение начинаем с того, что через любую вершину ΔАВС проводим линию параллельную перпендикуляру DК. На фронтальной плоскости (П 2) эта линия будет // (параллельна) D2К2, а на горизонтальной плоскости (П 1) - // D1К1. Отмечаем во фронтальной плоскости проекций (П 2) на только что проведенной // перпендикуляру D2К2 линии через вершину С2 любую произвольную точку Р2. Находим ее проекцию на горизонтальной плоскости проекций (П 1) на линии, проведенной через точку С1 параллельно перпендикуляру D1К1. Методом прямоугольного треугольника находим натуральную величину отрезка С2Р2. Для этого необходимо найти и измерить разность расстояний от точек С1 и Р1 до оси Х. На рис. 4 это расстояние обозначено буквой l. Теперь нужно возвратиться на фронтальную проекцию и провести перпендикуляр в точке С2 к отрезку С2Р2. На нем отложить отрезок l и конечную точку N2 соединить с точкой Р2. Полученный отрезок N2P2 и будет натуральной величиной отрезка С2Р2. Именно на отрезке N2P2 от точки N2 нужно отложить расстояние, равное 50 мм, и из конечной точки провести линию параллельную отрезку N2С2, которая пересечет отрезок С2Р2 в точке Т2 (бывают случаи, когда истинная величина отрезка С2Р2, т.е. отрезок N2С2, меньше, чем требуемое по условию задачи расстояние 50мм. Это не должно смущать студента, так как отрезок N2P2 можно продолжить за точку Р2, также как отрезок С2Р2).

Теперь, когда точка Т2, которая отстоит от плоскости ΔАВС на 50мм, найдена, нужно найти ее горизонтальную проекцию, используя проекционную связь. Точка Т1 будет располагаться на отрезке С1Р1. Далее необходимо задать плоскость, параллельную ΔАВС, используя свойство параллельности плоскостей, смысл, которого в следующем: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Возьмем две, пересекающиеся в точке С2, стороны С2В2 и С2А2 и через точку Т2 проведем прямые, одна из которых параллельна С2В2, а другая - С2А2. Ограничим угол В2С2А2 волнистой линией. Это будет плоскость, заданная двумя, пересекающимися в точке Т2, прямыми, параллельная ΔАВС. На горизонтальной плоскости проекций через точку Т1 проведем одну прямую, параллельную стороне С1В1, а другую прямую – параллельную С1А1. Полученный угол В1С1А1 ограничим волнистой линией. Таким образом, мы получили горизонтальную проекцию плоскости, параллельную ΔАВС, которая образована двумя пересекающимися прямыми.

 

Задача 3

В задаче 3 искомая плоскость, перпендикулярная к заданной, должна содержать в себе заданную прямую и перпендикуляр, опущенный из любой точки этой прямой на заданную плоскость. Точки пересечения заданной прямой и перпендикуляра определяют линию пересечения искомой и заданной плоскостей. Видимость плоскостей определяется при помощи конкурирующих точек скрещивающихся прямых, принадлежащих этим плоскостям.

Этап 5 (рис.5). Построения, выполняемые на этапе 5, повторяют построения, выполненные на этапах 1 и 2 и заключаются в построении перпендикуляров из точек D1 и D2 на проекции плоскости, заданной ΔАВС. Дело в том, что плоскость, которая должна пересечь ΔАВС, по условию задачи ей перпендикулярна, значит, одна из сторон новой плоскости, заданной скрещивающимися прямыми, должна являться перпендикуляром к ΔАВС. Точки К1 и К2 являются точками пересечения перпендикуляров, опущенных из точек D1 и D2 на горизонтальную и фронтальную плоскости ΔАВС. Эти точки являются началами отрезков, по которым будет проходить пересечение двух плоскостей. Но для построения плоскости необходимо ввести в наш чертеж точки Е1 и Е2.

 

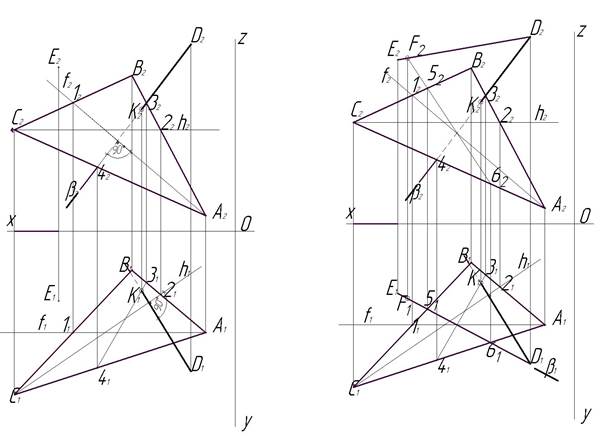
Рис.5. Этап 5 Рис. 6. Этап 6

 

Этап 6 (рис.6). На горизонтальной проекции через прямую D1 Е1 задаем секущую плоскость b и отмечаем точки пересечения D1 Е1 с ΔА1В1С1 - 51 и 61. Находим их соответствующие проекции на фронтальной плоскости – 52 и 62. Точки 52 и 62 соединяем между собой и продолжаем этот отрезок до пересечения с прямой Е2D2. Получили точку F2.

Этап 7 (рис.7). Соединяем точки F2 и К2 на фронтальной плоскости проекций, а также точки F1 и К1 на горизонтальной плоскости проекций. Отрезки F2 К2 и F1К1 – являются линиями пересечения заданной плоскости ΔАВС и искомой, перпендикулярной заданной.

 

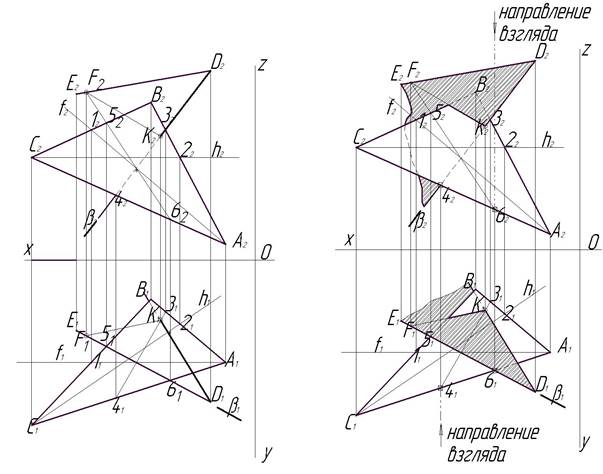
Этап 8 (рис.8). На последнем этапе необходимо определить видимость пересечения двух плоскостей. Это можно определить, используя метод конкурирующих точек скрещивающихся прямых, которым принадлежат эти точки.

 

 

Рис.7. Этап 7 Рис. 8 Этап 8

Возьмем точку 61, в которой скрещиваются прямые С1А1 и Е1D1, и подымем проекционную связь на фронтальную плоскость проекций. По этой проекционной связи проследим сверху вниз расположение прямых С2А2 и Е2D2. Нас интересует, какая из этих прямых встретится на нашем пути (сверху вниз) раньше. Первой мы встречаем прямую Е2D2, а затем прямую С2А2. Из этого можно сделать вывод, что на горизонтальной проекции из двух рассматриваемых скрещивающихся прямых выше лежит прямая Е1D1. Это значит, что в этой плоскости проекций плоскость, заданная пересекающимися прямыми Е1D1 и К1D1,находится выше плоскости, заданной ΔАВС, значит, в этом месте она будет видимой до линии пересечения F1К1, а ΔАВС – невидимым.

Чтобы определить видимость пересекающихся плоскостей на фронтальной плоскости проекций, возьмем точку 42. В этой точке скрещиваются прямые С2А2 и D242. Опустим проекционную связь из этой точки на горизонтальную проекцию. И проследим, какая из прямых С1А1 и D141 встретится нам раньше, если смотреть на них снизу вверх. Как видно из чертежа, первой встречается С1А1, а затем D141. Это говорит о том, что на фронтальной проекции (с которой мы начинали свое исследование) ΔАВС, которому принадлежит прямая С1А1, будет видимым, плоскость, заданная пересекающимися прямыми Е1D1 и К1D1, – невидимой. Для более наглядного изображения нужно заштриховать одну из пересекающихся плоскостей и показать невидимые стороны плоскостей пунктирной линией.

 

 

Рис.9. Пример выполнения эпюра №1

 

ЭПЮР 2. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ (пример 1)

Содержание эпюра.

Даны пирамида и плоскость общего положения, требуется:

задача 1 – построить линию пересечения пирамиды с плоскостью и определить видимость фигур;

задача 2 – определить истинную величину сечения.

Образец выполнения эпюра №2 представлен на рисунке 14.

 

Указания к выполнению эпюра

Данные взять из Приложения (задания к эпюру №2). Считать секущие плоскости непрозрачными. Истинную величину сечения определить любым способом. Это может быть способ замены плоскостей проекций, плоскопараллельное перемещение, вращение, совмещение.