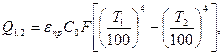Теплообмен излучением системы тел в прозрачной среде

Рассмотрим теплообмен между двумя единичными поверхностями, обращенными друг к другу с небольшим зазором, причем Т₁>Т₂. В этой системе Е₁ – энергия собственного излучения первого тела на второе, Е₂ – второго на первое. Ввиду малого расстояния между ними практически все излучение каждой из рассматриваемых поверхностей попадает на противоположную. Воспользуемся понятием эффективного излучения Е_эф, представленного выражением

Е_эф=Е+RE_пад.

Для непрозрачного тела (D=0 и R=1-A) выражение Е_эф=Е+RE_пад запишется в виде Е_эф=Е+E_пад(1-А).

Каждое из рассматриваемых тел имеет эффективное (полное) излучение, соответственно Е_эф1 и Е_эф2. Для первого тела Е_эф2 является падающим излучением, поэтому

Е_эф1=Е_эф1+Е_эф2(1-А₁)

Аналогично для первого тела

Е_эф2=Е_эф2+Е_эф1(1-А₂)

Плотность результирующего теплового потока от первого тела на второе равна

q_1,2=Е_эф1-Е_эф2

Подставляя найденные из совместного решения уравнений выражение Е_эф1 и Е_эф2 в формулу q_1,2=Е_эф1-Е_эф2 получаем

Заменим величины Е₁ и Е₂ по формуле Е=e×Е₀=e×С₀(Т/100)⁴=С(Т/100)⁴. Тогда

Будем считать что степень черноты обеих поверхностей не меняется в диапазоне температур от Т₁ до Т₂. Следовательно по закону Кирхгофа А₁=e₁ и А₂=e₂. Заменяя А на e и вынося e₁e₂с₀, получаем:

величина =e_пр называется приведенной степенью черноты системы тел. С учетом e_пр и выражения формула для полного топливного потока записывается в виде

где F – площадь теплообменной поверхности одинаковая в нашем случае для обоих тел.

Из =e_пр видно, что e_пр меняется от нуля до единицы, оставаясь всегда меньше e₁ и e₂.

В соответствии с формулой полный поток теплоты, передаваемый излучением от горячего тела более холодному, пропорционален поверхности тела, приведенной степени черноты и разности четвертых степеней абсолютных температур тел.

На практике часто наблюдается одна теплообменная поверхность полностью охватываемая другой. В отличии от теплообмена между близко расположенными поверхностями с равными площадями здесь лишь часть излучения поверхности F₂ попадает на F₁. Остальная энергия воспринимается самой же поверхностью F₂. Тепловой поток, передаваемый излучением от внутреннего тела к внешнему, можно также определить по формуле если вместо F подставить поверхность меньшего тела F₁, а степень черноты системы определить по формуле:

В случае теплообмена между произвольными телами каждое из них излучает на другое лишь часть энергии, излучаемой им по всем направлениям; остальная энергия рассеивается в пространстве или попадает на другие тела. В этом случае в расчетную формулу вводится поправочный коэффициент, называемый коэффициентом облученности тела j_1,2 и учитывающий долю излучения первого тела, которая воспринимается вторым телом.

Таким образом, теплообмен между двумя произвольно расположенными телами может быть рассчитан по формуле