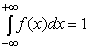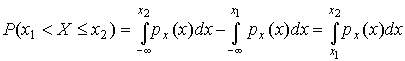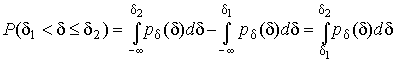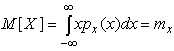Описание случайных погрешностей с помощью функций распределения

 

Рассмотрим результат наблюдений Х за постоянной физической величиной Q как случайную величину, принимающую различные значения Z, в различных наблюдениях за ней. Значения Xi будем называть результатами отдельных наблюдений.

Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения [1].

Под интегральной функцией распределения результатов наблюдений понимается зависимость вероятности того, что результат наблюдения Xi в i -м опыте окажется меньшим некоторого текущего значения х, от самой величины х:

Fx (x) = P (Xi ≤ x) (4)

Здесь и в дальнейшем большие буквы используются для обозначения случайных величин, а маленькие — значений, принимаемых случайными величинами. Поскольку функция распределения вероятности представляет собой вероятность, то она удовлетворяет следующим свойствам:

• 0 ≤ Fx (x) ≤ 1 при x ∈ (–∞, +∞),

• Fx (–∞) = 0, Fx (+∞) = 1,

• Fx (x) — неубывающая функция x,

• P(x 1 < X < x 2) = FX (x 2) – FX (x 1).

На рис.2 показаны примеры функций распределения вероятности.

Более наглядным является описание свойств результатов наблюдений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей:

f (x) = dFX (x)/ dx (5)

Физический смысл f(x) состоит в том, что произведение f(x)dx представляет вероятность попадания случайной величины Х в интервал от х до х + dx, т.е.

f (x) dx = P (x ≤ X ≤ x+dx) (6)

Свойства плотности распределения вероятности:

— вероятность достоверного события равна 1;

иными словами, площадь, заключенная между кривой дифференциальной функции распределения и осью абсцисс, равна единице;

— вероятность попадания случайной величины в интервал от x 1 до x 2.

От дифференциальной функции распределения легко перейти к интегральной путем интегрирования:

(7)

Размерность плотности распределения вероятностей, как это следует из формулы (7), обратна размерности измеряемой величины, поскольку сама вероятность — величина безразмерная.

Используя понятия функций распределения, легко получить выражения для вероятностей того, что результат наблюдений Х или случайная погрешность δ примет при проведении измерения некоторое значение в интервале [ x 1, x 2] или [δ1, δ2].

В терминах интегральной функции распределения имеем:

P (x 1 < X ≤ x 2) = P -∞ < X ≤ x2 – P-∞ < X ≤ x 1 = Fx (x 2) – Fx (x 1)

P (δ1 < δ ≤ δ2) = P -∞ < δ ≤ δ2 – P-∞ < δ ≤ δ1 = F δ(δ2) – F δ(δ1)

т.е. вероятность попадания результата наблюдений или случайной погрешности в заданный интервал равна разности значений функции распределения на границах этого интервала.

Заменяя в полученных формулах интегральные функции распределения на соответствующие плотности распределения вероятностей согласно выражению (7), получим формулы для искомой вероятности в терминах дифференциальной функции распределения:

(8)

(9)

Таким образом, вероятность попадания результата наблюдения или случайной погрешности в заданный полуоткрытый интервал равна площади, ограниченной кривой распределения, осью абсцисс и перпендикулярами к ней на границах этого интервала. Необходимо отметить, что результаты наблюдений в значительной степени сконцентрированы вокруг истинного значения измеряемой величины и по мере приближения к нему элементы вероятности их появления возрастают. Это дает основание принять за оценку истинного значения измеряемой величины координату центра тяжести фигуры, образованной осью абсцисс и кривой распределения, и называемую математическим ожиданием результатов наблюдений:

(10)

В заключение можно дать более строгое определение постоянной систематической и случайной погрешностей.

Систематической постоянной погрешностью называется отклонение математического ожидания результатов наблюдений от истинного значения измеряемой величины:

θ = M [ X ] – Q (11)

а случайной погрешностью — разность между результатом единичного наблюдения и математическим ожиданием результатов

δ = X – M[ X ] (12)

В этих обозначениях истинное значение измеряемой величины составляет

Q = X – θ – δ (13)